VAEs
本学习笔记用于记录我学习Stanford CS236课程的学习笔记,分享记录,也便于自己实时查看。
潜变量
对于生成模型,我们可以试图寻找一组潜变量z,这个潜变量可以有具体含义,例如对于人脸生成模型的眼睛,鼻子,嘴巴等。通过修改这些潜变量我们可以得到不同风格的生成对象。但是对于图片或者自然语言而言,人为指定这种潜变量极为困难。
所以我们可以并不人为指定潜变量的含义,例如无监督学习的GMM(高斯混合聚类)就并没有指定每个类别具体的含义。但高斯混合聚类人为指定了类别的数量,这对于生成模型也是很难实现定义的。
对于GMM来说,事实上是定义了一组离散的潜变量,在每个潜变量下的数据分布服从高斯分布,它可以给我们一些启示,虽然每个类别的概率只是定义为正态分布,但它组合之后可以形成非常复杂的概率分布。
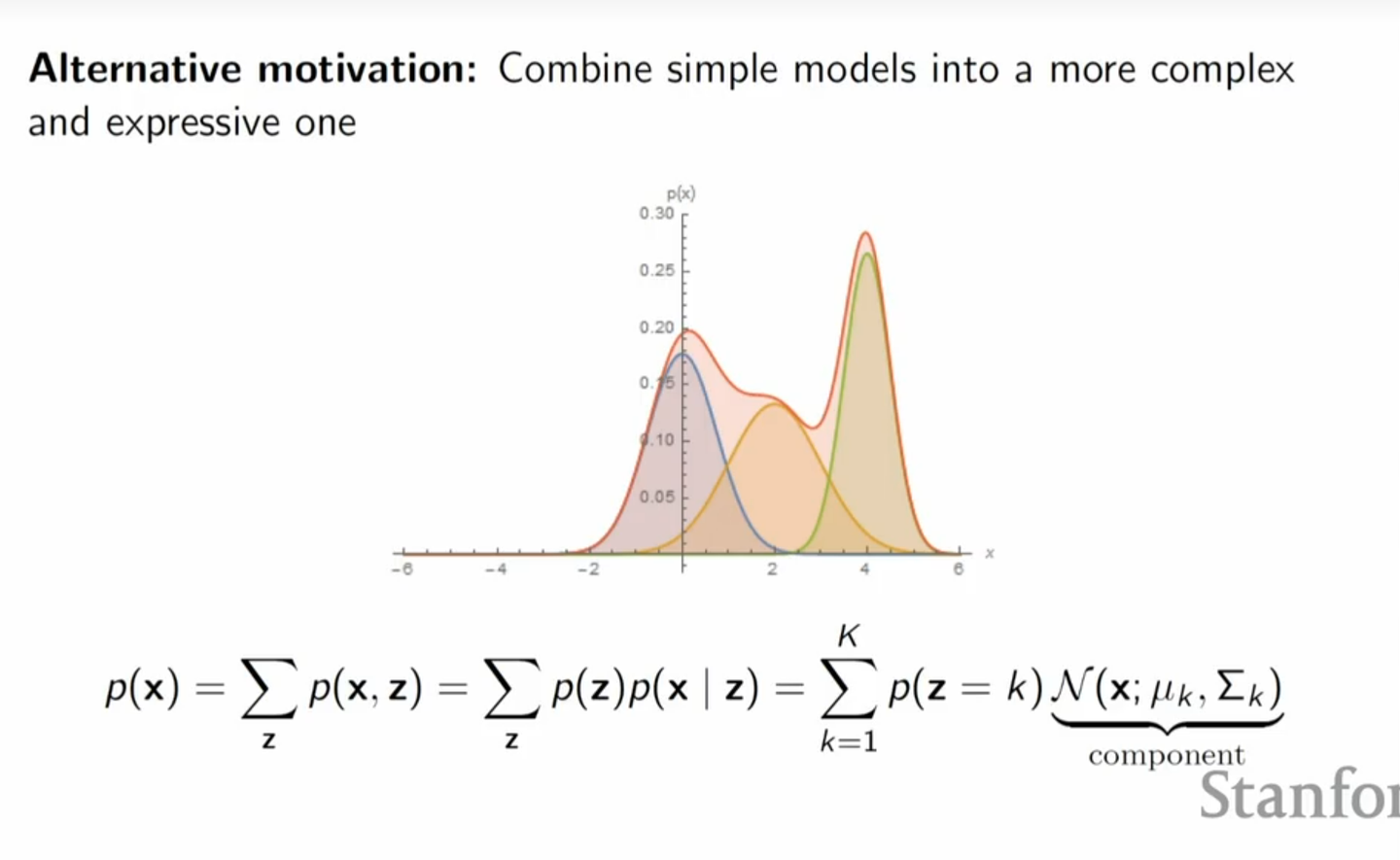
所以不妨我们可以设定有无穷多个高斯聚类的组合,即设定潜变量 z
是一个连续的随机变量,而每个潜变量 z
的值对应于一个高斯分布,事实上这也正是VAEs做的
核心思想
VAE 的目标是学习一个生成器,将随机向量\(z \in R^d\)映射到\(x \in R^D\), 使得\(x\)的分布尽可能接近真实数据的分布。
这里的\(z\)其实就是上面提到的潜变量,他是一个连续的随机变量,实践中一般定义为服从高斯分布。而对于每个z的值,我们假设x的分布是满足均值为\(\mu(z)\),协方差矩阵为\(\Sigma(z)\)(可以通过神经网络进行学习)的高斯分布。理论上这样的组合可以逼近任意的概率分布。
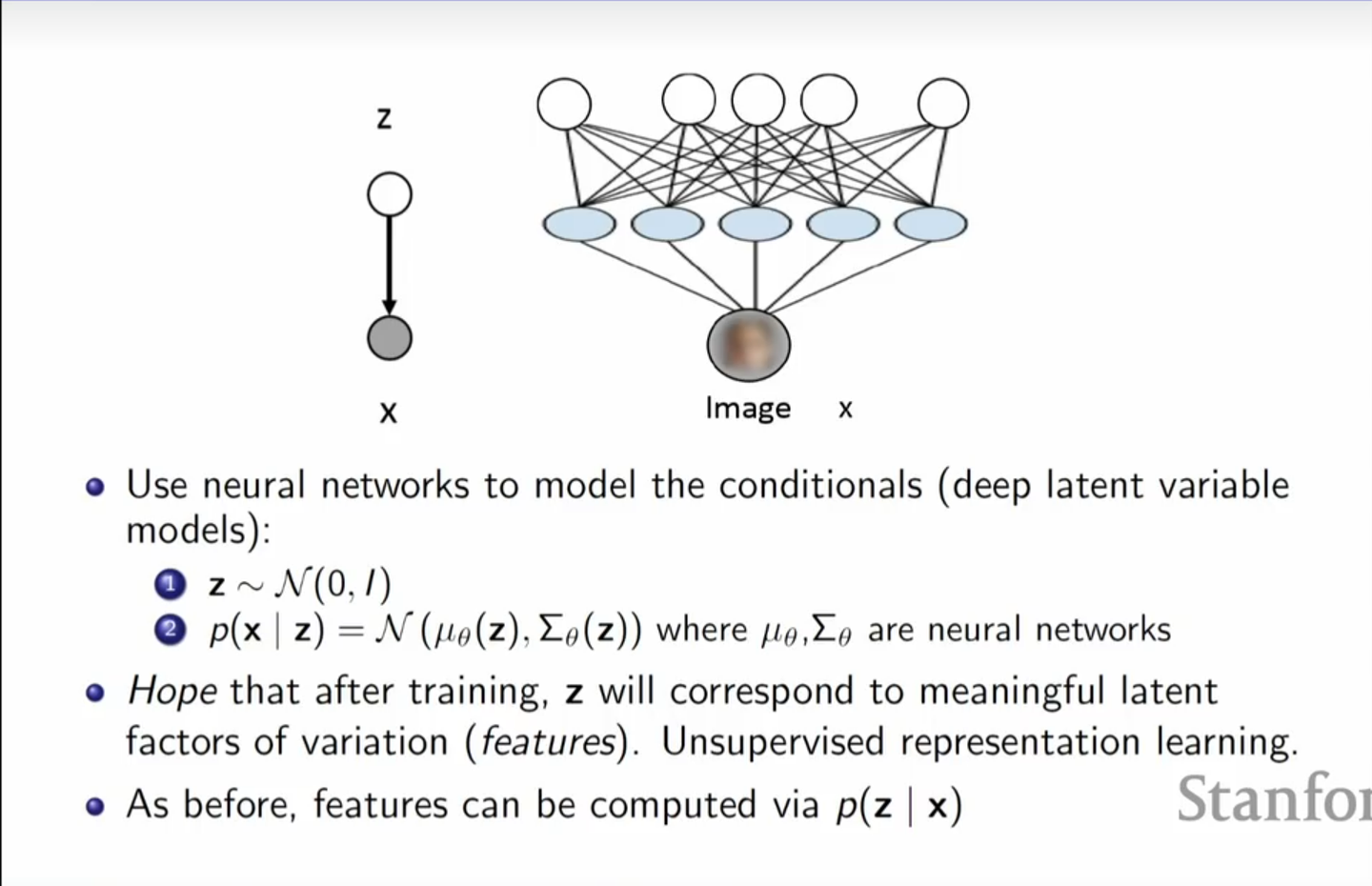
当然PPT中的\(z\sim N(0,
I)\)只是一个例子,也可以有更复杂的定义,但在实践中一般使用标准正态分布。
生成和训练
损失函数
对于一个生成模型来说,生成和评估的难易很大程度上决定了它的实用性和价值。对于上面VAE的假设来说,生成是很简单。即假设我们已经知道了\(p(x|z)\),我们只需要先采样\(z\),再采样\(x\) 就能得到数据。
但是评估并不容易,这意味着模型的训练可能是一个棘手的问题。对于评估,既然是衡量两个分布的相似度,我们能否直接用各种散度(如 KL 散度)作为损失函数呢?当然可以。在蒙特卡洛抽样(Monte Carlo Sampling)下,最小化KL散度就是最大似然估计。
那么我们的目标是\(θ_∗=argmax \sum_{i=1}^{n} logp_θ(x_i)\),注意到
\(\sum logP_\theta(x) =\sum log(\sum q(z)P_\theta(x|z))\)
对于等式右边的计算是非常复杂的,因为\(z\)的取值理论上具有无穷多个

所以我们需要对这个公式进行简化,注意到
\[ \begin{align} P_\theta(x) &= \sum (q(z) \frac{p_\theta(z, x)}{q(z)}) \nonumber \\ &= E_{z \sim q(z)}\left(\frac{p_\theta(z,x)}{q(z)}\right) \end{align} \]
通过蒙特卡洛抽样(Monte Carlo Sampling),我们可以从\(q(z)\)中采样若干数据点,然后进行平均即可估计\(P_\theta(x)\)的值。但很可惜,我们无法通过蒙特卡洛抽样来估计\(log(P_\theta(x))\), 因为
\(log(E_{z \sim q(z)}(\frac{p_\theta(z,x)}{q(z)})) \ne E_{z \sim q(z)}(log(\frac{p_\theta(z,x)}{q(z)}))\)

但幸运的是,对于对数函数是一个严格的凹函数,所以对于凹函数来说有
\(log(px + (1-p)x^{'}) \geq plogx +(1-p)logx^{'}\),进一步扩展便就是著名的琴生不等式:

琴生不等式
因此\(log(E_{z \sim q(z)}(\frac{p_\theta(z,x)}{q(z)})) \geq E_{z \sim q(z)}(log(\frac{p_\theta(z,x)}{q(z)}))\)
所以我们可以通过这种方法来估计似然的下限,即上面不等号的右边,叫做ELBO(Evidence Lower Bound)

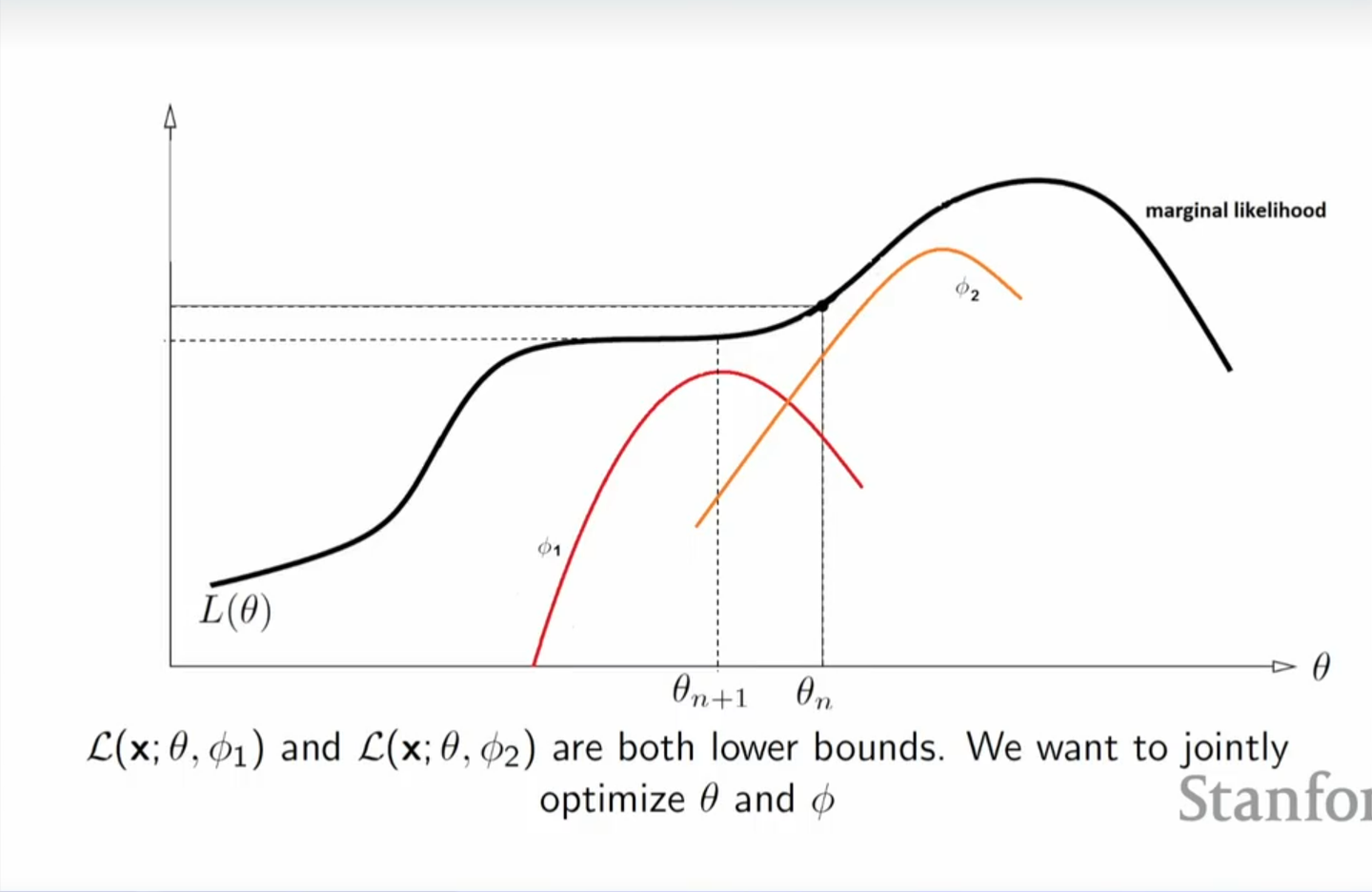
至于这个界限有多紧,我们对\(logP(x)\)进行一下推导,就能得到它们之间相差的便是\(D_{KL}(q(z)||p(z|x;\theta)\),也就是说当\(q(z)\)与我们的后验分布越接近,这个界限越紧。

其实这里的推导就是EM算法里面的推导,最大化ELBO的过程就是对应于EM算法里面的M步(后续有机会可能也会写一写)。非常可惜的是,EM
算法无法直接应用于此,因为 E-step 要求我们能够表达出后验分布\(p_\theta(z|x)\),但没关系,如果我们能够最大化ELBO,也能保证似然的下限被最大化。
问题似乎解决了,但值得注意的是,ELBO 是关于函数\(q\)的泛函,也就是说\(q\)可以取任意函数,这并不好直接优化。为了解决这个问题,我们可以将\(q(z)\)限制为以\(\phi\)为参数的某可解分布族\(q_\phi(z|x)\) ,这样优化变量就从函数\(q\)变成了参数\(\phi\)。不过,由于我们限制了\(q\)的形式,所以即便能求出最优的参数\(\phi\),也大概率不是\(q\)的最优解。显然,为了尽可能逼近最优解,我们应该让选取的分布族越复杂越好。

那么这里有一个小问题——为什么\(q(z)\)参数化后写作\(q_\phi(z|x)\)而不是\(q_\phi(z)\)?
首先,\(q\)本来就是我们人为引入的,它是否以\(x\)为条件完全是我们的设计,且并不与之前的推导冲突;其次,ELBO与似然当\(q(z)=p_θ(z|x)\)时是完全等价的,可见对于不同的\(x\),其\(q(z)\)的最佳形式是不同的,所以这么设定有利于减少ELBO与似然的距离。
在VAE中 的\(p_θ(x|z)\)和\(q_\phi(z|x)\)都由神经网络表示,因此我们用梯度下降来最大化
ELBO 即可。即对ELBO取负数就是最终的损失函数。

注意到这样的形式中并没有\(p_θ(x|z)\)一项,我们只需要稍微变化一下:
\[ \begin{align} L(x;\theta, \phi) &= \sum q_{\phi} (z|x)\left[\log(p_{\theta}(z,x;\theta)) - \log(q_{\phi}(z|x))\right] \\ &= \sum q_{\phi} (z|x)\left[\log(p_{\theta}(z,x;\theta)) - \log(p(z)) + \log(p(z)) - \log(q_{\phi}(z|x))\right] \\ &= \sum q_{\phi} (z|x)\left[\log(p_{\theta}(x|z)) - \log\left(\frac{q_{\phi}(z|x)}{p(z)}\right)\right] \\ &= E_{z \sim q_{\phi}(z|x)}\left[\log(p_{\theta}(x|z))\right] - D_{KL}(q_{\phi}(z|x) || p(z)) \end{align} \]
这里就把我们的目标分成了两项:
- 第一项是重构项,要求我们尽可能重构数据本身
- 第二项是正则项,要求我们的后验与先验接近
所以可以看到,它与自动编码器最大的区别在于有第二项,这保证了隐藏变量\(z\)的分布,从而我们可以从先验中对\(z\)取样从而进行生成。换句话来说,VAEs是对潜变量进行了正则化的自动编码器,因为我们知道了潜变量\(z\)的分布形式,所以它能够用于生成。
按照蒙特卡洛抽样(Monte Carlo Sampling),理论上求这个期望需要对每个样本多次采样进行计算,最后平均。但在具体实践中,往往采样一次进行计算就行。
梯度计算细节:重参数化技巧
有一个细节是现在\(z\)是从
\(q_\phi(z|x)∼N(μ_ϕ(x),diag(\sigma^{2}_ϕ(x)))\)
中采样的,但梯度无法经过采样传播到参数\(\phi\)。但其实解决方法很简单,对于高斯函数,只需要先从\(N(0,I)\)中采样\(\epsilon\)再计算\(z=μ_ϕ(x)+\epsilon⋅σ_ϕ(x)\)即可。
这种技巧也叫做重参数化技巧,其最开始应该是在强化学习中出现的,后面有时间也可以写一写。
