Normalizing Flows
本学习笔记用于记录我学习Stanford CS236课程的学习笔记,分享记录,也便于自己实时查看。
引入
生成模型模型的目的是让得到的数据分布\(P_{\theta}\)与真实的数据分布\(P_{data}\)相同,也就是需要通过给定的样本来建模对应的分布,使得输入经过该模型后可以生成与给定样本类似的新样本。在这种意义下,评估的最佳方式便是使用极大似然估计,然而VAEs的做法导致计算似然十分复杂,所以我们只能选择计算似然的下界,也就是ELBO。
不妨思考一下,VAEs无法计算似然的原因是什么。不难发现,关键在于需要对所有的潜变量\(z\)进行积分。所以假如我们有一个可逆映射,使得潜变量\(z\)和数据\(x\)之间的是一一对应的,那我们便可以很轻松计算似然了。
Normalizing Flows正是这么做的。但可逆映射意味着潜变量\(z\)的维度需要和数据\(x\)的维度一致,所以我们无法利用\(z\)进行压缩。
简介
正则化流(Normalizing Flow)是一种可逆生成模型,用于将一个原始分布通过学习的变换映射到另一个已知的概率分布。它可以将数据从原始分布转换为目标分布,从而实现数据的生成和采样。
在正则化流中,我们定义一个变换函数,它将输入样本从原始分布映射到目标分布。这个映射是一个可逆函数,确保转换是可逆的,也就是说,在给定目标分布样本的情况下,可以逆向计算出原始分布的样本。这个变换函数通常由一系列的可逆操作组成,每个操作都是可逆的,并且通过组合这些操作可以得到整个变换。常用的可逆操作包括仿射变换、尺度变换、平移变换等。
原理
变量替换
变量替换的形式如下:\(p_{X}(X)=p_{Z}(f(X))|det~J(f(X))|\)
\(Z=f(X)\)是一个可逆的变换 \(J(f(X))\)是\(f(X)\)的雅可比行列式
如何理解呢:即给出一个\(X\),使用一个可逆变换\(f(\cdot)\)将\(X\)变为\(Z\),那么\(p(X)、p(Z)\)这两个分布之间相差的就是这样一个雅可比行列式。

流的组合
基本原理:可导的可逆的函数在进行组合后依然是一个可导且可逆的函数
标准化方向:\(f=f_{1}\circ f_{2}\circ....f_{N}\)
采样构造概率的方向:\(g=g_{N} \circ g_{N-1} \circ .... \circ g_{1}\)
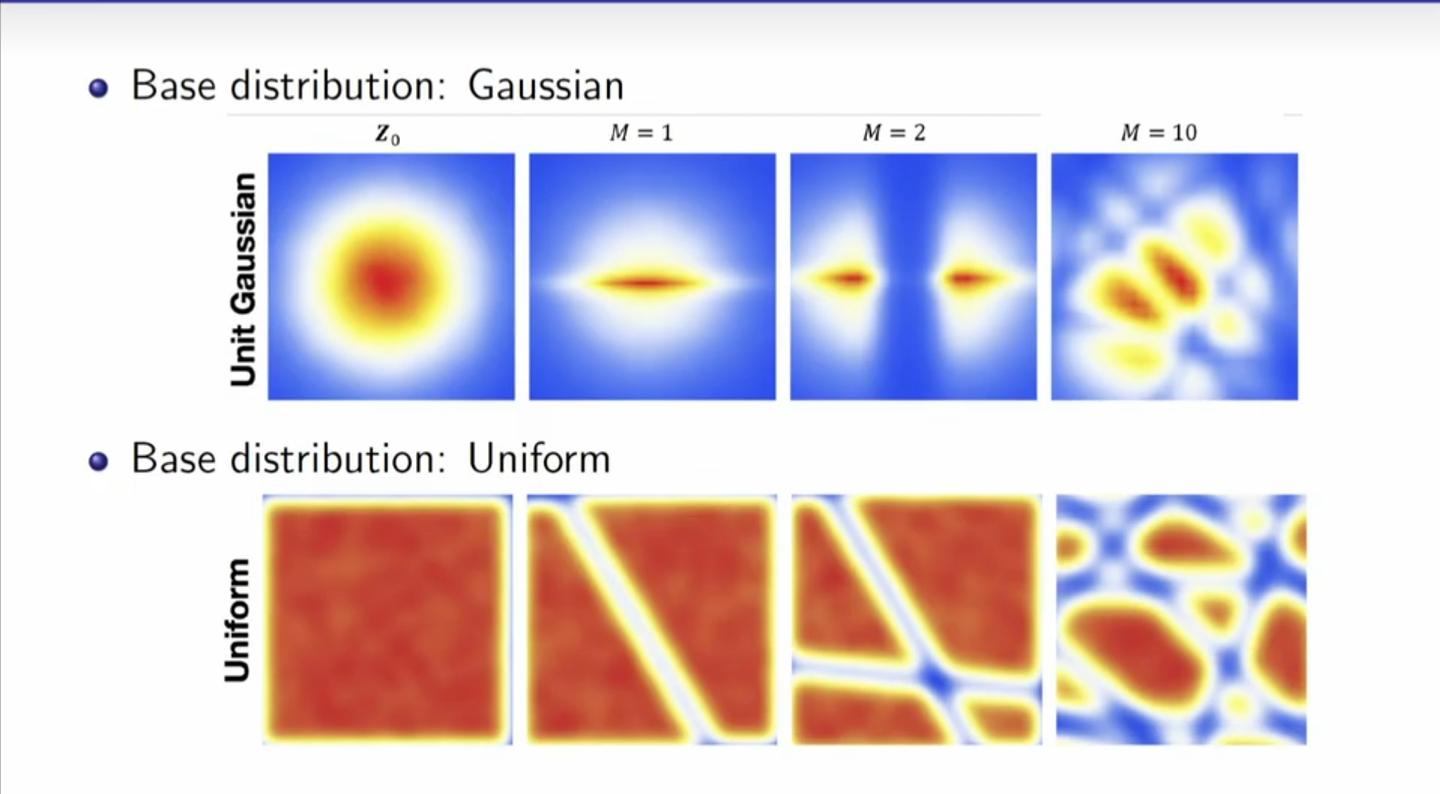
这种流动的感觉就是标准化流这个名字的由来。
而由\(p_{X}(X)=p_{Z}(f(X))|det~J(f(X))|\)可知,上面组合出来的\(f\)的雅可比行列式刚好可以表示为每一个\(f_{i}\)的雅可比行列式相乘再求行列式。
\(det~J(f)=det\prod_{i=1}^{N}J(f_{i})=\prod_{i=1}^{N}det~J(f_{i})\)
因为每一个样本都是独立同分布采样出来的,所以它的log likelihood就是把他们的每一个log likelihood加起来。由于做过变量代换,就可以把它变成我们知道的非常简单的分布加上剩下的log 雅可比行列式的和。

计算
通过最大似然估计,我们便可以训练模型了。但问题在于,如何构建这种可逆映射和如何让雅可比行列式方便计算。因为对于一般的雅可比行列式的计算复杂度是\(O(n^3)\),但是我们可以构造半三角的雅可比行矩阵,这样行列式的计算复杂度只有\(O(n)\)了
NICE: Non-linear Independent Components Estimation
NICE的目标是找到一个transformation\(z=f(x)\), 将数据映射到一个新的空间中; 这个空间中的\(z\)的各个分量\(z_d\)之间都是独立的, 即\(p_\theta(z)=\prod_d p_{\theta_d}(z_d)\).在这种"各分量独立"的假设下, 模型会自发地学习"most important factors of variation"; 否则, 比如\(h_1\)和\(h_2\)之间不独立, 那么就浪费了一部分建模能力, 从而无法达到最好的建模效果.
通过\(z\)的先验分布和\(x=f^{-1}(z)\), 可以实现\(x\)的生成(采样)。一般可以假定\(z\)的分布满足标准高斯分布。
映射构造(Additive coupling layer)
如何构造构造半三角的雅可比行矩阵呢?NICE给出的方法是:
\(z_{1\sim d} = x_{1\sim d}\)
\(z_{ {d\sim D} } = x_{ {d\sim D} } + u_{\theta}(x_{ {1\sim d} })\)
这个变换的雅克比矩阵为
\[ \frac{\partial z}{\partial x}=\left[ \begin{array}{cc} I_d & \bar{0} \\ [\frac{\partial u_\theta}{\partial x_{1\sim d} }] & I_{n-d} \\ \end{array} \right] \]
这个映射的逆变换也很简单,为
\(x_{1\sim d} = z_{1\sim d}\)
\(x_{ {d\sim D} } = z_{ {d\sim D} } - u_{\theta}(z_{ {1\sim d} })\)
Combining coupling layers
事实上, 这个\(f\)是要用很多层叠在一起得到的, 即\(f=f_L \circ ... \circ f_2 \circ f_1\)。 在堆叠coupling layer的时候, 注意到每个变换有一部分输入是不变的。这样才能让所有部分都能得到变换. 即, 第一层\(z_1=x_1\), 变\(x_2\), 那么第二层就\(z_2=x_2\), 变\(z_1\).
另外, 堆叠后的雅克比行列式为
\[ \left|\det \frac{\partial z}{\partial x} \right| = \left|\det \frac{\partial f_L(x)}{\partial f_{L-1}(x)}\right| \cdot \left|\det \frac{\partial f_{L-1}(x)}{\partial f_{L-2}(x)}\right| \cdot \ldots \cdot \left|\det \frac{\partial f_2(x)}{\partial f_1(x)}\right| \]
这些行列式的绝对值为1。
Allowing scaling
因为每个行列式的绝对值都是1, 因此\(f\)是volume preserving(体积不变的)的. 为了消除这个限制, 在\(f_L\)后又乘了一个diagonal scaling matrix\(S\), 即\(z=S \cdot f_{1, ...,L}(x)\). 这样既可以让一些重要特征又更大的变化范围, 又可以让一些不重要的特征减小变化范围(降维). 所以最后目标函数为
\(\log p_X(x)=\sum_{i=1}^D [\log p_{H_i}(f_i(x)) + \log |S_{ii}|]\)
Density Estimation Using Real NVP
Real NVP将NICE中的每一层的映射改为如下:
\(\begin{aligned} z_{1:d}&=x_{1:d}\\ z_{d+1:D} &=x_{d+1:D} \odot exp(s(x_{1:d})) +t(x_{1:d}) \end{aligned}\)
逆变换为
\(\begin{aligned} x_{1:d}&=z_{1:d}\\ x_{d+1:D} &=(z_{d+1:D}- t(x_{1:d})) \odot exp(-s(x_{1:d})) \end{aligned}\)
这个变换的雅克比矩阵为
\[ \frac{\partial z}{\partial x}=\left[ \begin{array}{cc} I_d & \bar{0} \\ \frac{\partial z_{d+1:D} }{\partial x_{1:d} } & diag(exp(s(x_{1:d}))) \\ \end{array} \right] \]
其中\(diag(exp(s(x_{1:d})))\)是将\(exp(s(x_{1:d}))\)这个向量展开为对角矩阵. 这个雅克比矩阵的log-determinant为 \[\prod_{i=1}^d \log \exp(s(x_{1:d}))=\sum_{i=1}^d s(x_{1:d})\] 其中没有任何\(s\)和\(t\)行列式的计算, 因此二者可以任意复杂且hidden layer采用不同于输入的维度.
这样我们便完成了一个更加复杂的构造,同时它的表现也自然比NICE更好。