GANs
本学习笔记用于记录我学习Stanford CS236课程的学习笔记,分享记录,也便于自己实时查看。
引入
前面我们学习了VAEs和Normalizing Flows,这两种模型都是基于最小化KL散度(对似然进行评估)来进行优化的。我们也可以看到,为了进行生成,我们往往会定义一个潜变量\(z\),所以对似然进行评估并不容易。VAEs是通过优化似然的下限ELBO来绕过这个问题,而Normalizing Flows是通过限制映射的形式来计算似然。
直接计算似然来进行评估,要么只能计算其下界,要么需要限制映射的形式。那有没有一种方法能够用间接方法代替这种直接比较,使生成分布变得越来越接近真实分布呢?GANs便是基于一种间接的评估方式进行设计的。
基本思想
GANs的间接方法采用这两个分布的下游任务形式。然后,生成网络的训练是相对于该任务进行的,使生成分布变得越来越接近真实分布。GANs 的下游任务是区分真实样本和生成样本的任务。或者我们可以说是“非区分”任务,因为我们希望区分尽可能失败。
因此,在 GANs 架构中,我们有一个判别器,它接收真实和生成数据样本,并尽可能地对它们进行分类;还有一个生成器,它被训练成尽可能地欺骗判别器。即GANs由2个重要的部分构成:
- 生成器(Generator):通过机器生成数据,目的是“骗过”判别器。
- 判别器(Discriminator):判断数据是真实的还是生成的,目的是找出生成器做的“假数据”。
训练过程
我们知道GANs的思想后,便能很直观的想到用分类问题的交叉熵作为判别器的损失函数。同时生成器的目的则是最大化这个交叉熵损失函数(混淆判别器),所以我们的训练目标是:
\[\mathop{\text{min}}\limits_{G}\mathop{\text{max}}\limits_{D} \ V(G,D) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log(1 - D(G(z)))]\]
其中\(G\)指的是生成器,\(D\)指的是判别器。
所以我们的训练目标是一个极大极小的优化问题,在实际中,我们只需要从数据集中进行采样,然后用生成器进行采样,然后对上面的目标函数进行近似计算,最后进行梯度上升或者梯度下降即可

与散度的关系
那么为什么这样的设计能够间接地去让生成器生成的样本与真实样本的分布相同呢?
其实本质上,GANs通过引入判别器来间接地计算了\(\frac{P_\theta(x)}{P_{data}(x)}\),可以证明,对于一个生成器下的最佳判别器对给定\(x\)的判定为真实样本的概率是\(\frac{P_{data}(x)}{P_{data}(x) + P_\theta(x)}\), 证明如下:
*Proof*: 二分类交叉熵损失函数为:
\[\begin{align} \mathrm{BCE}(\mathcal P_1,\mathcal P_2)&=-\mathbb E_{x\sim \mathcal P_1}[\log D(x)]-\mathbb E_{x\sim \mathcal P_2}[\log(1-D(x))]\\ &=-\int \log D(x)\cdot p_1(x)\mathrm d x-\int\log(1-D(x))\cdot p_2(x)\mathrm d x\\ &=-\int \left[\log D(x)\cdot p_1(x)+\log(1-D(x))\cdot p_2(x)\right]\mathrm d x\\ \end{align} \\\]
易知\(y=a\log x+b\log(1-x)\)在\(x=\frac{a}{a+b}\)处取到唯一极大值(其中\(0\leq a,b\leq1\)),所以欲使上式最小,只需:
\(\forall x,\,D(x)=\frac{p_1(x)}{p_1(x)+p_2(x)} \\\)这样就证明完成了。
那么,再看我们的训练目标:
\[\min_G\max_D V(G, D) \\ \begin{align} V(G, D)&=\mathbb E_{x\sim\mathcal P_{data}}[\log D(x)]+\mathbb E_{z\sim \mathcal P_z}[\log(1-D(G(z)))]\\ &=\mathbb E_{x\sim\mathcal P_{data}}[\log D(x)]+\mathbb E_{x\sim \mathcal P_{\theta}}[\log(1-D(x))] \end{align} \\\]
而最优判别器为:
\(D^\ast(x)=\frac{p_{data}(x)}{p_{data}(x)+p_\theta(x)} \\\) 将最优判别器代入\(G\)的优化目标:
\[\begin{align} V(G, D^\ast)&=\mathbb E_{x\sim \mathcal P_{data}}\left[\log\frac{p_{data}(x)}{p_{data}(x)+p_\theta(x)}\right]+\mathbb E_{x\sim \mathcal P_\theta}\left[\log\frac{p_\theta(x)}{p_{data}(x)+p_\theta(x)}\right]\\ &=2\mathrm {JS}(\mathcal P_{data}\|\mathcal P_\theta)-2\log2 \end{align} \\\]
因此,生成器实际上在最小化\(\mathcal P_{data}\)和\(\mathcal P_\theta\)的\(\mathrm{JS}\)散度,从而让生成数据的分布\(\mathcal P_\theta\)接近真实分布\(\mathcal P_{data}\)。
注:\(JS\)散度的定义如下:
*\[\begin{align} \mathrm{JS}(\mathcal P_1\|\mathcal P_2)&=\frac{1}{2}\left[\mathrm{KL}\left(\mathcal P_1\|\mathcal P_A\right)+\mathrm{KL}\left(\mathcal P_2\|\mathcal P_A\right)\right]\\ &=\log 2+\frac{1}{2}\mathbb E_{x\sim\mathcal P_1}\left[\log\frac{p_1(x)}{p_1(x)+p_2(x)}\right]+\frac{1}{2}\mathbb E_{x\sim\mathcal P_2}\left[\log\frac{p_2(x)}{p_1(x)+p_2(x)}\right] \end{align} \\\]
其相比\(KL\)散度最大的特点便是其是对称的*。

可以看出GANs是通过判别器来巧妙地规避了计算似然的问题,但正是因为在实践中我们很难得到真正的最佳判别器,所以实际上我们很多时候只是在优化\(JS\)散度的一个下界,笔者认为这是GANs不得不直面的一个问题。
fGAN
F-散度(F-divergence)
在概率统计中,f散度是一个函数,这个函数用来衡量两个概率密度\(p\)和\(q\)的区别,也就是衡量这两个分布多么的相同或者不同。像\(KL\)散度和\(JS\)散度都是它的一种特例
f散度定义如下:
\[{D_f}(\mathcal P_1\|\mathcal P_2)=\int f (\frac{p_2(x)}{p_1(x)})\cdot p_1(x)\mathrm d x=\mathbb E_{x\sim\mathcal P_1}\left[f(\frac{p_2(x)}{p_1(x)})\right] \\\]\(f(·)\)就是不同的散度函数,\(D_f\)就是在f散度函数下,两个分布的差异。规定
\(f\)是凸函数(为了用琴生不等式) \(f ( 1 ) = 0\)(如果两个分布一样,刚好公式=0)

这两个规定保证了\(D_f\)是非负的,而且当两个分布相同时,其值为0,一些常见散度的\(f\)定义如下:

共轭函数(Fenchel Conjugate)
一个函数\(f:\;\mathbb{R}^n\mapsto\mathbb{R}\)的 Frenchel 共轭为:
\[\begin{align} f^*( t)=\sup_{ x}\big(\langle t, x\rangle-f( x)) \end{align}\]
Fenchel 共轭有几何上的解释。当\(x\)固定时,\(\langle t, x\rangle-f( x)\)是一个仿射函数,因此 Fenchel 共轭就是一组仿射函数的上确界。如果\(f\)可微,那么仿射函数取得上确界的位置正好是\(f\)的切线,此处有\(\nabla f( x)= t\)。
我们拿\(f ( x ) = x l o g x\)来说,当\(x=10,1, 0.1\)时可以看到相应的函数直线,可以看到最大化y的点连起来是个凸函数,很类似\(e^{t-1}\)
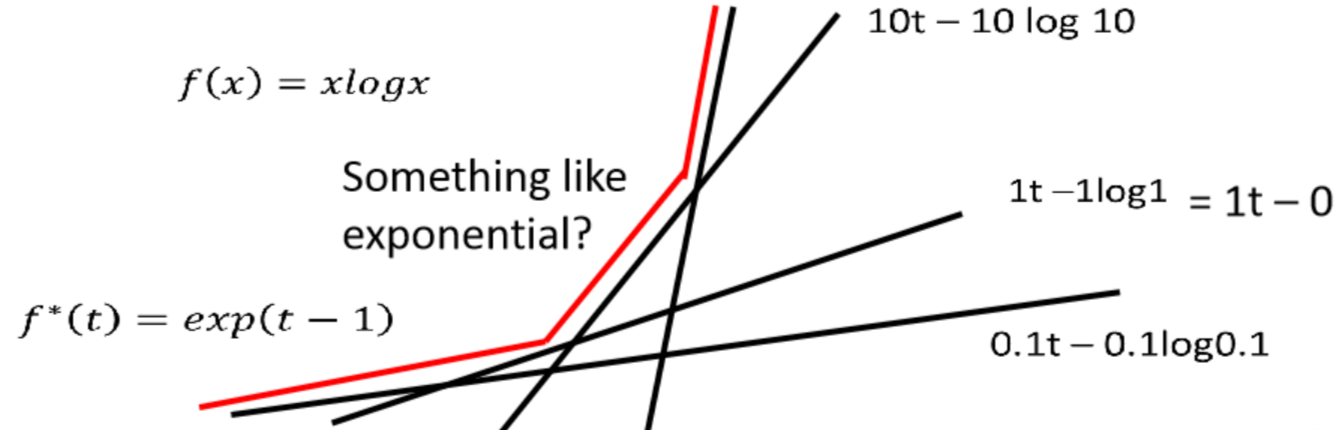
公式图像:
用数学来推一下:
将\(f ( x ) = x l o g x\)代入\(y ( t ) = x t − f ( x )\),得\(y ( x ) = x t − x l o g x\),对于每个给定的\(t\)都可以求出最大值,求导为0即可。
求导后得:\(t − l o g x − 1 = 0\),即\(x=e^{t-1}\),代入\(f^*(t)\), 得\(f^*(t)=te^{t-1}-e^{t-1}(t-1)=e^{t-1}\)
读者可以对这个\(f^*(t)\)再求一次共轭,可以发现其又变回原函数了。
事实上,可以证明,对于凸函数来说\(f^{**}(x) = f(x)\)

应用于GAN
那这个跟GAN有啥关系呢?
假如我们用一个\(D_f\)来评估生成模型,对于\(p(x)\)和\(q(x)\)之间的 f-divergence:
\[\begin{aligned} D_f(P||Q) &= \int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) dx \\ &= \int_{x} q(x) \left( \max_{t \in \operatorname{dom}(f^*)} \left\{\frac{p(x)}{q(x)}t - f^*(t)\right\} \right) dx \end{aligned} \]
记一个函数 D(x),它输入是\(x\),输出是\(t\),用该函数代替上式中的\(t\),得到
\[\begin{aligned} D_f(P||Q)&\geq\int \limits_{x}q(x)(\frac{p(x)}{q(x)}D(x)-f^{*}(D(x)))dx\\ &= \int \limits_{x}p(x)D(x)dx-\int \limits_{x}q(x)f^{*}(D(x))dx \end{aligned}\]
D(x) 其实就是判别器,可以看出,它依然是在解一个求最大值问题,通过这种方法,去逼近 f-divergence。
\[D_f(P||Q)\approx\max \limits_{D}\int \limits_{x}p(x)D(x)dx-\int \limits_{x}q(x)f^{*}(D(x))dx\]
p(x) 和 q(x) 本质上是一个概率,于是有
\[D_f(P||Q)\approx\max \limits_{D}\{E_{x\sim P}[D(x)]-E_{x\sim Q}[f^*(D(x))]\}\]
用\(P_{data}\)和\(P_\theta\)来指代 P 和 Q,有
\[D_f(P_{data}||P_\theta)\approx\max \limits_{D}\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_\theta}[f^*(D(x))]\}\]
有没有发现这一套下来很熟悉?其实这还是我们之前训练生成器判别器的那一套流程。也就是
\[\begin{aligned} G^*&=\mathop{argmin} \limits_{G}D_f(P_{data}||P_\theta)\\&=\mathop{argmin} \limits_{G}\max \limits_{D}\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_\theta}[f^*(D(x))]\}\\&=\mathop{argmin} \limits_{G}\max \limits_{D}V(G, D) \end{aligned}\]
只不过这次的损失函数更加 general 了。换不同的\(f(x)\),就可以量不同的散度(divergence)。

WGAN
JS散度 to Wasserstein(Earth-Mover EM)距离
JS散度的问题
考虑两个分布"完全不相交"的时候,会发现\(JS\)散度为常量,梯度为\(0\)无法优化。
下面一个例子来说明:
假设两个二维空间上的概率分布,记为\({P}_d(X_1, Z)\)和\({P}_g(X_2, Z)\)。我们刻画\(Z \sim U(0, 1)\)一个\([0, 1]\)上的均匀分布,而分别令\(X_1 = 0\)和\(X_2
=
\theta\),因而,它们在二维空间上的概率分布空间就是两条平行线(垂直于\(x\)的轴,而平行于\(z\)的轴)。
当\(\theta =
0.5\)时,我们考量等价于JS散度的损失函数\(V(G,
D^*)\),由于两个分布概率大于0的空间范围是完全没有重叠的,因此,对于任意\(p_d(x,y) \ne 0\)必然有\(p_g(x, y) =0\)成立,反之亦然。
因而我们就有,对于任意\(x \in
\mathbb{R}^2\),
\[V(G, D^*)= \int_x p_d(x) log
\frac{p_{d}(x)}{p_{d}(x) + p_{g}(x)} + p_g(x)log
\frac{p_{g}(x)}{p_{d}(x) + p_{g}(x)} dx \\ = \int_x p_d(x) log (1) +
p_g(x)log (1) dx = 0
\\\]此时,损失函数恒为常量,无法继续指导生成器\(G(x)\)的优化。即此时出现了梯度消失的问题。
Wasserstein距离
为了弥补JS散度的局限性,我们需要一种全新的”分布间距离“的度量来进行优化,即使用Wasserstein距离,也被称为“推土机距离”(Earth-Mover),它定义如下:
\(W({P}_d, {P}_g) = inf_{\gamma \in \Pi({P}_d,
{P}_g)} {E}[||x - y||]
\\\)这样数学形式的刻画可能会让人看得颇为一头雾水,我们逐步来分析解释它。
其中,\(\Pi({P}_d, {P}_g)\)代表一个\({P}_d, {P}_g\)构成的联合分布的集合,且这个集合中的所有联合分布必须满足其边际分布分别为\({P}_d, {P}_g\)。\(||x-y||\)是两个分布所在空间\(\mathbb{R}^n\)中两点的欧式距离。
我们可以将\(\Pi({P}_d, {P}_g)\)中的元素理解为一种“概率的搬运方案”。 而\(\gamma\)是上述集合中的一个联合分布,可以使得任意两点的欧式距离期望最小,即将一个分布搬运为另外一个分布的最小开销。
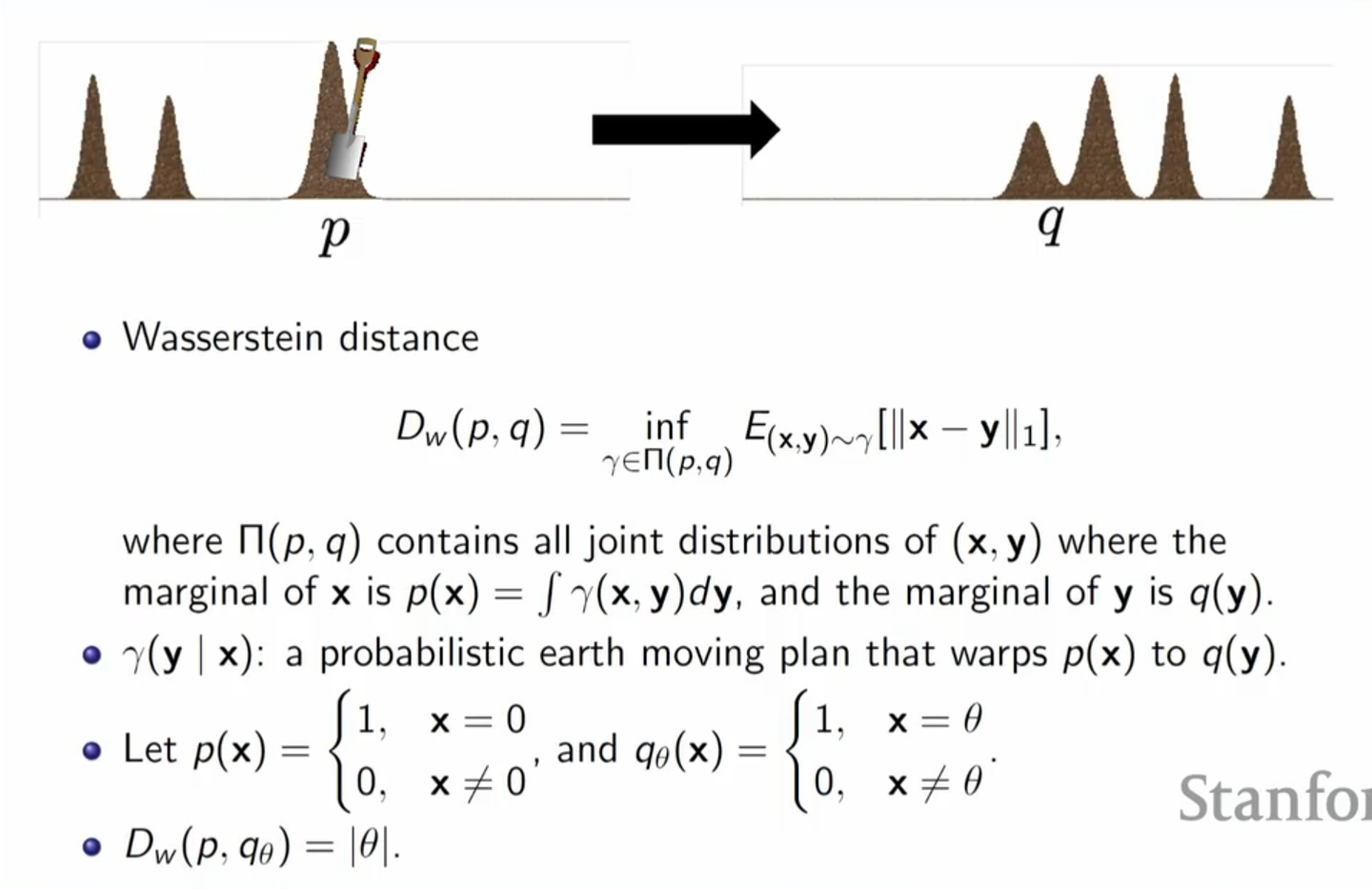
此时,我们再重新观察上面的场景,当概率分布式为两条平行线上的均匀分布时,显然,最佳方案就是直接与x轴平行地进行概率搬运,对应为:\(W(P_0, P_\theta) =
|\theta|\)。此时,即使两个分布完全没有重叠部分,我们仍然能通过优化Wasserstein距离来实现两个概率分布之间的距离优化。
可以给出证明的是,就像JS散度一样,Wasserstein距离收敛于0时,两个分布也完全一致。
固然,通过Wasserstein距离优化GAN的想法颇为"美好",不过,找到"最优搬运方案"的优化问题却是难事,在实现层面上,我们难以直接计算Wasserstein距离。不过,基于对偶理论可以将Wasserstein距离变换为积分概率度量IPM框架下的形式,来方便我们进行优化。
IPM也是用于衡量两个分布之间的距离,它的想法是寻找某种限制下的函数空间\(\mathbb{F}\)中的一个函数\(f(·)\),使得对任意位置两个分布的差异最大:
\[d_F(p, q) = sup_{f \in F} \mathbb{E}_{x \sim P}[f(x)] - \mathbb{E}_{x \sim Q}[f(x)] \\\]对于Wasserstein距离而言,则变为:
\[W(p, q) = sup_{||f||_L \le 1} \mathbb{E}_{x \sim P}[f(x)] - \mathbb{E}_{x \sim Q}[f(x)] \\\]因而,在函数\(f(·)\)满足Lipschitz约束的函数空间中,即\(||f(x) - f(y)|| \le K||x - y||\),找到最佳的函数\(f(·)\),该情况下上式的结果则为Wasserstein距离。
这个函数\(f(·)\)难以求解,但我们可以用神经网络来拟合它。需要注意的是,从此开始,GAN的\(D\)就不再是先前我们认为的“真假判别器”了,它的意义变成了一个距离的度量。此时,GAN的生成器并不改变仍然生产图片,对生成器的训练则是减小与真实分布的Wasserstein距离,判别器\(D\)负责给出真实图像和生产图像样本之间的Wasserstein距离,相应的,在固定生成器优化判别器时,化则变为了寻找函数空间\(\mathbb{F}\)中最佳的\(f(·)\)。

下面的图就可以体现传统GAN的判别器梯度和WGAN的判别器梯度的区别
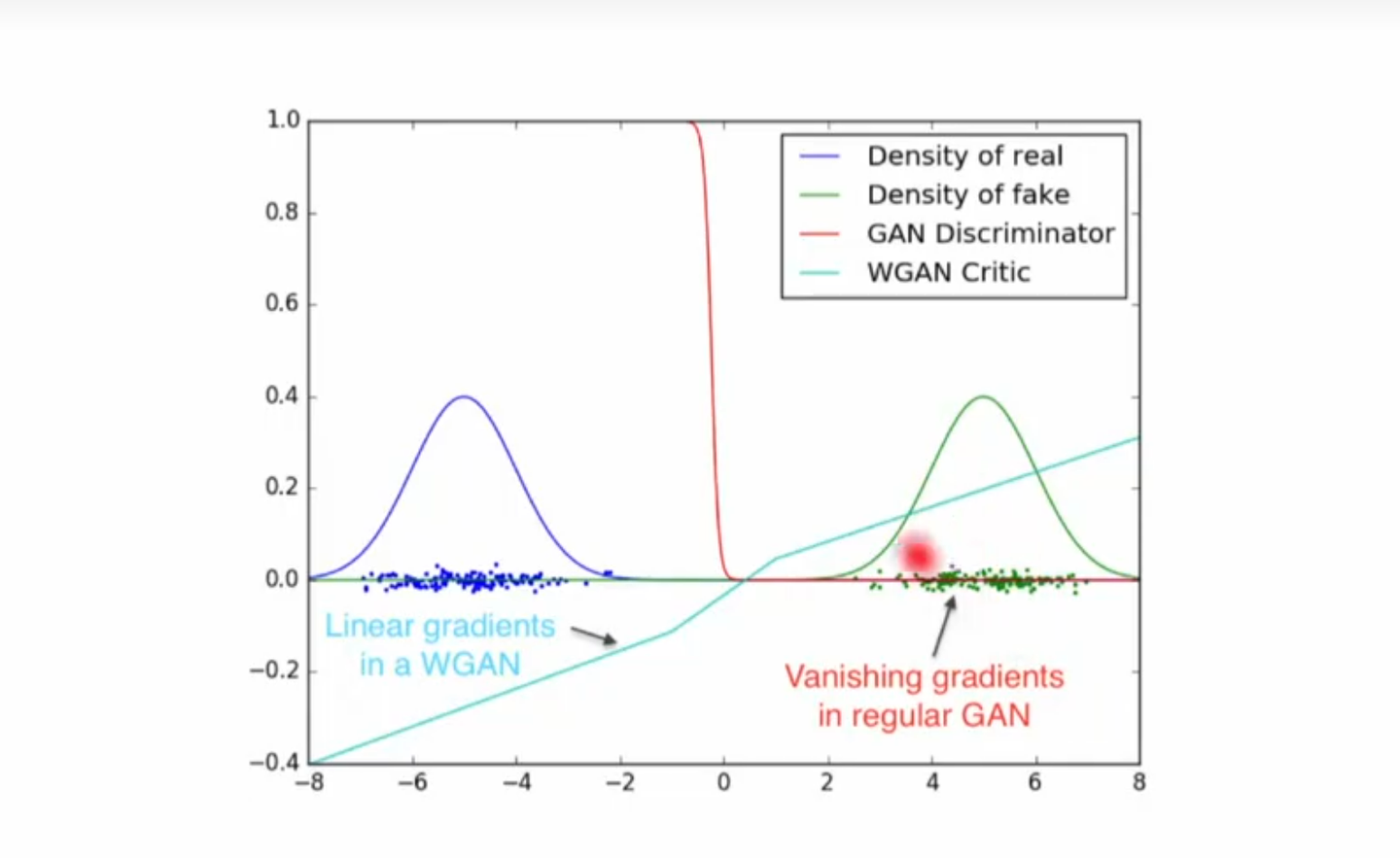
WGAN便有效解决了某些情况下传统GAN的梯度消失的问题