蒙特卡洛采样方法

最近在学习Stanford CS236课程，里面多次提到了蒙特卡洛采样，但本人之前并没有系统地对蒙特卡洛采样进行过整理学习，所以也就正好趁此机会学习一下蒙特卡洛采样，分享记录，也便于自己实时查看。

蒙特卡洛估计

蒙特卡洛估计的原理

蒙特卡洛估计(Monte Carlo Estimator)的原理很简单，假设现在我们要求解一个一维的积分 \(\int_{a}^{b} g(x) dx\) 。已知一个概率密度为 \(f(x)\) 的随机变量\(X\) ，蒙特卡洛估计可以表示为：

\[G_N = \frac{1}{N}\sum_{i=1}^{N}{\frac{g(X_i)}{f(X_i)}}\\\]

概率密度 \(f(x)\) 需要满足

\[ \begin{cases} f(x) > 0, x \in (a, b),\\ f(x) = 0, x \notin (a, b).\end{cases}\\\]

现在来验证下, 这种方式是正确的：

\[\begin{align*} E[G_N] & =E\left [ \frac{1}{N}\sum_{i=1}^{N}{\frac{g(X_i)}{f(X_i)}} \right]\\ & = \frac{1}{N}\sum_{i=1}^{N}\int_{a}^{b}\frac{g(x)}{f(x)}f(x)dx\\ &= \frac{1}{N}\sum_{i=1}^{N}\int_{a}^{b}g(x)dx\\ &= \int_{a}^{b}g(x)dx \end{align*}\\\]

也就是说， \(G_N\) 的期望与 \(\int_{a}^{b} g(x) dx\) 是相同的，而 \(G_N\) 的方差如下：

\[\begin{align*} D[G_N] & =D\left [ \frac{1}{N}\sum_{i=1}^{N}{\frac{g(X_i)}{f(X_i)}} \right]\\ & = \frac{1}{N^2}D\left [ \sum_{i=1}^{N}{\frac{g(X_i)}{f(X_i)}} \right]\\ &= \frac{1}{N^2}\cdot N \cdot D\left [ {\frac{g(X_i)}{f(X_i)}} \right]\\ &= \frac{1}{N} D\left [ {\frac{g(X_i)}{f(X_i)}} \right] \end{align*}\\\]

从上面的式子，可以看出，要减少方差，有两种途径：

• 增加采样次数 \(N\)
• 减少 \(D(\frac{g(X)}{f(X)})\)

理论上，只要我们采样次数足够多，方差趋近于0，\(G_N\) 也就依概率收敛于\(\int_{a}^{b} g(x) dx\)

蒙特卡洛估计的优点

我们在考虑一个积分算法/Estimator 时，通常从两个角度考虑。

一个是计算的准确性，即随着采样次数增大时，结果是否趋近于我们期望的真实值。如果一个 estimator 的期望值和真实值相等，我们说它是无偏的/unbiased。如果一个 estimator 的期望值和真实值不相等，则它是有偏的。大部分 estimator 都是无偏的，在少数情况下，我们会使用一个有偏的但是计算收敛速度很快的 estimator。

另外一个角度是计算结果的方差。随着采样次数增大时，计算结果的方差应该总是减少的。两个estimator 的方差可以比较可以从两个角度来体现。即采样次数相同时的方差大小，以及随着采样次数增大，方差收敛的速度。我们总是期望使用一个方差较小且收敛较快的 estimator，来减少计算的事件。

计算结果表明，蒙特卡洛估计误差收敛的速度为 \(O(\sqrt N)\) (意味着4倍的采样会使误差减少一半)，蒙特卡洛估计不受维度影响，在高维情况下比其他估计方法收敛要快得多。

蒙特卡洛估计的实践使用

在实际使用中，直接使用蒙特卡洛方法要求我们能够从 \(p(x)\)中采样——对于简单分布（如均匀分布）这是容易做到的；对于稍微复杂一些但可写出 PDF 或 CDF 分布，可以利用变量替换定理来直接采样；而对于更复杂的分布，我们则更多选择拒绝采样和重要性采样来实现这一点。。

变量替换定理

$ X$ 服从一个我们能直接进行采样的连续值（例如均匀分布），我们希望找到一个函数 \(f(x)\) ，让 \(Y=f(X)\) 满足我们需要得到的分布 \(Y \sim P_y\) ，则使用累积分布函数：

\[P_y(y)\triangleq P(Y\le y)=P(f(X)\le y)=P(X\in(f(x)\le y))\]

概率密度函数可以通过累积分布函数求导得到。当单调，因此可逆时，可得：

\[P_y(y)=P(f(X)\le y)=P(X\le f^{-1}(y))=P_x(f^{-1}(y))\]

求导可得：

\[p_y(y)\triangleq\frac{d}{dy}P_y(y)=\frac{d}{dy}P_x(f^{-1}(y))=\frac{dx}{dy}\frac{d}{dx}P_x(x)=\frac{dx}{dy}p_x(x)\]

其中 \(x=f^{-1}(y)\) 。由于符号并不重要，因此可得一般表达式：

\[p_y(y)=p_x(x)|\frac{dx}{dy}|\]

可将上述结果拓展为多变量分布。令 \(f\) 为 \(R^n\) 到 \(R^n\) 的映射， \(\mathrm y=f(\mathrm x)\) 。则雅可比矩阵 \(J\) 为：

\[J_{\mathrm x\rightarrow\mathrm y}\triangleq\frac{\partial(y_1,\ldots,y_n)}{\partial(x_1,\ldots,x_n)}\triangleq \begin{pmatrix} \frac{\partial y_1}{\partial x_1} &\dots&\frac{\partial y_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial y_n}{\partial x_1}&\dots&\frac{\partial y_n}{\partial x_n} \end{pmatrix}\]

\(|det J|\) 度量了单位立方体在应用 \(f\) 时的体积变化量。如果 \(f\) 是一个可逆映射，可以使用反映射 \(\mathrm y\rightarrow\mathrm x\) 的雅可比矩阵定义变换变量的概率密度函数：

\[p_y(\mathrm y)=p_x(\mathrm x)|\det\left(\frac{\partial \mathrm x}{\partial\mathrm y}\right)|=p_x(\mathrm x)| \det J_{\mathrm y\rightarrow\mathrm x}|\]

这就是随机变量的变量替换定理，通过这个我们可以对一些相对简单的分布进行直接采样了。

例如设 \(x\) 服从累积分布函数为 \(F(x)=1-e^{-x}\) (可验证是单调不减，且积分为1的函数)的分布，则可以通过逆变换的方法对 \(F(x)\) 直接采样，产生服从F(X)分布的样本X。
令 \(y=1-e^{-x}\)，则$ e^{-x}=1-y$.两边求对数可得: \(x=-ln(1-y)\) ,则 \(F^{-1}(x)=-ln(1-x)\) ，令 \(x_i\) 为均匀分布样本，则 \(X_i=-ln(1-x_i)\) 为服从累积分布函数为\(F(x)\) 分布的样本.

拒绝接受采样

拒绝接受采样的目的仍然是得到服从某个概率分布的样本，不过这种方法是直接利用概率密度函数(PDF)得到样本。如下图所示， \(p(x)\) 是我们希望采样的分布， \(q(x)\) 是我们提议的分布(proposal distribution)， \(q(x)\) 分布比较简单，令 \(kq(x)>p(x)\) ，我们首先在 \(kq(x)\) 中按照直接采样的方法采样粒子，接下来以 \(\frac{p(x_i)}{kq(x_i)}\) 的概率接受这个点，最终得到符合 \(p(x)\) 的N个粒子。

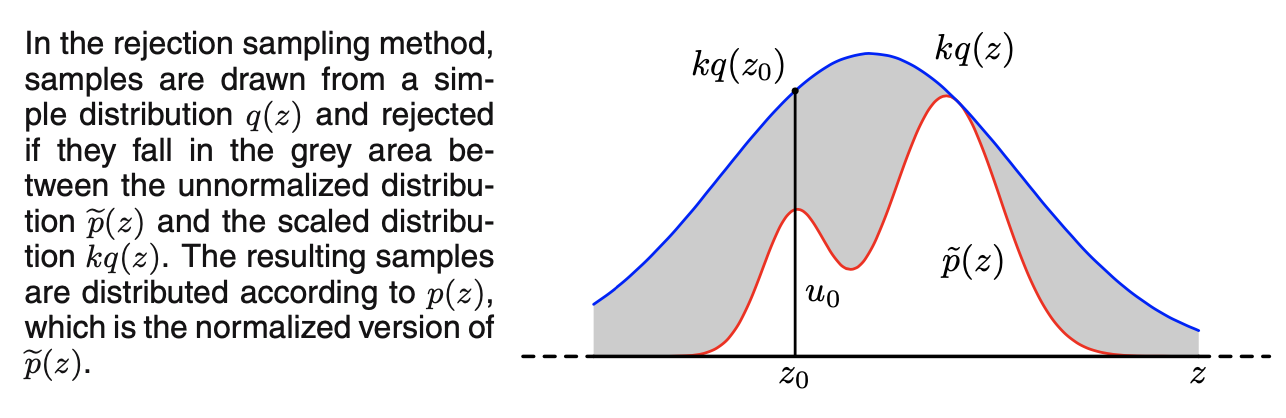
可以证明，这样做得到的样本是服从\(p(x)\)的，我们可以计算 \(x_0\) 对应的样本被取到的概率为：

\[\frac{q(x_0)\dfrac{\tilde p(x_0)}{kq(x_0)}}{\displaystyle\int_x q(x)\frac{\tilde p(x)}{kq(x)}\mathrm dx}=\frac{\tilde p(x_0)}{\displaystyle\int_x \tilde p(x)\mathrm dx}=p(x_0)\]

所以拒绝接受采样的基本步骤：

1. 生成服从 \(q(x)\) 的样本 \(x_i\) .
   
2. 生成服从均匀分布 \(U(0,1)\) 的样本 \(u_i\) .
   
3. 当 \(k\cdot q(x_i)\cdot u_i<p(x_i)\) ,也就是二维点落在蓝线以下，此时接受 \(X_k=x_i\) 这里乘以 \(u_i\) ，是因为我们需要以 \(\frac{p(x_i)}{kq(x_i)}\) 的概率接受这个点，因为如果 \(k\cdot q(x_i)\cdot u_i<p(x_i)\) ，则 \(u_i<\frac{p(x_i)}{k\cdot q(x_i)}\) ，而 \(u_i\) 服从均匀分布 \(U(0,1)\)
4. 最终得到的 \(X_k\) 为服从 \(p(x)\) 的样本.

我们可以计算一下样本采样的接受率：

\[p(\text{accept})=\int_x \frac{\tilde p(x)}{kq(x)}q(x)\mathrm dx=\frac{1}{k}\int_x\tilde p(x)\mathrm dx\]

因此 \(k\) 越小，总接受率越大，算法效率越高。然而， \(k\) 小也意味着 \(q(x)\) 本身就要与 \(p(x)\) 比较相似，对于复杂的 \(p(x)\) 而言寻找到一个合适的 \(q(x)\) 非常困难的。

重要性采样

重要性采样的目的：求一个函数 \(f(x)\) 在概率密度函数为\(p(x)\) 分布下的期望，即

\[\mathbb{E}[f(x)]=\int f(x)p(x)dx\]

当 \(p(x)\) 很复杂时，不解析，积分不好求时，可以通过重要性采样来计算。当 \(f(x)=x\) ，则可以算 \(p(x)\) 的期望。

原理

首先, 当我们想要求一个函数 \(f(x)\) 在区间 \([a, b]\) 上的积分 \(\int_{a}^{b} f(x) d x\) 时有可能会面临一个问题, 那就是积分曲线难以解析, 无法直接求积分。这时候我们可以采用一种估计的方式, 即在区间 \([a, b]\) 上进行采样: \(\left\{x_{1}, x_{2} \ldots, x_{n}\right\}\) , 值为 \(\left\{f\left(x_{1}\right), f\left(x_{2}\right), \ldots, f\left(x_{n}\right)\right\}\)

如果采样是均匀的, 即如下图所示:

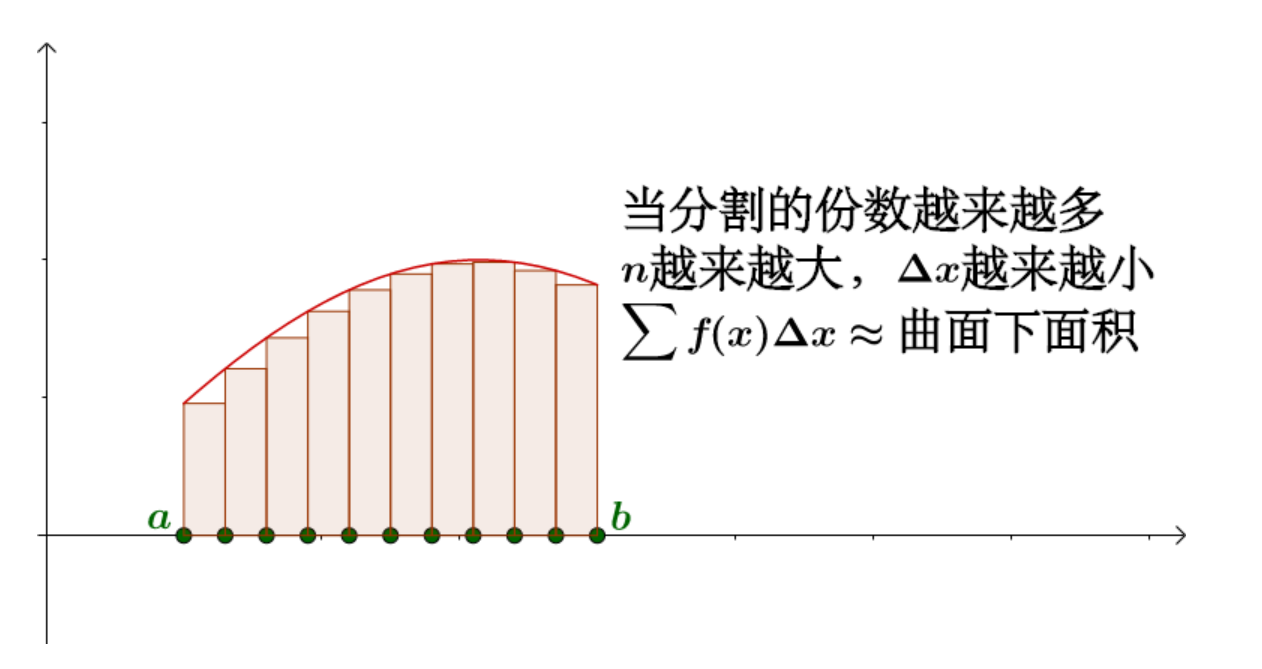
那么显然可以得到这样的估计: \(\int_{a}^{b} f(x) d x=\frac{b-a}{N} \sum_{i=1}^{N} f\left(x_{i}\right)\) , 在这里 \(\frac{b-a}{N}\) 可以看作是上面小长方形的底部的 “宽”, 而 \(f\left(x_{i}\right)\) 则是坚直的 “长”。

上述的估计方法随着取样数的增长而越发精确，那么有什么方法能够在一定的抽样数量基础上来增加准确度，减少方差呢？比如 \(x\) 样本数量取10000，那么显然在 \(f(x)\) 比较大的地方，有更多的 \(x_i\) ，近似的积分更精确。

并且原函数 \(f(x)\) 也许本身就是定义在一个分布之上的, 我们定义这个分布为 \(p(x)\) , 我们无法直接从\(p(x)\) 上进行采样, 所以另辟蹊径重新找到一个更加简明的分布 \(q(x)\) , 从它进行取样, 希望间接地求出 \(f(x)\) 在分布 \(p(x)\) 下的期望。

若p(x)归一化

搞清楚了这一点我们可以继续分析了。首先我们知道函数 \(f(x)\) 在概率分布 \(p(x)\) 下的期望为:

\[\mathbb{E}[f(x)]=\int_{x} p(x) f(x) d x \]

但是这个期望的值我们无法直接得到, 因此我们需要借助 \(q(x)\) 来进行采样, \(q(x)\) 可以选取简单的分布，比如设q(x)为均匀分布，当我们在 \(q(x)\) 上采样得到 \(\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\) （即 \(x_i\) 服从 \(q(x)\) 分布）后，那么我们可以估计 \(f\) 在 \({q(x)}\) 下的期望为：

\[\mathbb{E}[f(x)]=\int_{x} q(x) f(x) d x \approx \frac{1}{N} \sum_{i=1}^{N} f\left(x_{i}\right) \]

上面这个式子就简单很多了，只要我们得到 \(x_i\) 然后代入 \(f(x)\) 然后求和就行了，而且均匀分布的样本 \(x_i\) 很容易获得。接着我们来考虑原问题，对式(1)进行改写, 即： \(p(x) f(x)=q(x) \frac{p(x)}{q(x)} f(x)\) , 所以我们可以得到:

\[\mathbb{E}[f(x)]=\int_{x} q(x) \frac{p(x)}{q(x)} f(x) d x\]

这个式子我们可以看作是函数 \(\frac{p(x)}{q(x)} f(x)\) 定义在分布 \(q(x)\) 上的期望, 当我们在 \(q(x)\) 上采样 \(\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\) (服从q(x)分布)，可以估计 \(f\) 的期望:

\[\begin{aligned}\mathbb{E}[f(x)]&=\frac{1}{N} \sum_{i=1}^{N} \frac{p\left(x_{i}\right)}{q\left(x_{i}\right)} f\left(x_{i}\right)\\&=\frac{1}{N} \sum_{i=1}^{N} w_i f\left(x_{i}\right)\end{aligned}\]

在这里 \(w_i=\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\) 就是重要性权重。

若p(x)没有归一化

上面的讨论是假设 \(p(x)\) 已经完成归一化了，也就是 \(\int p(x)=1\) ,假如 \(p(x)\) 没有归一化，那么我们可以在上面的推导中对 \(p(x)\) 进行归一化：

\[\begin{aligned}\mathbb{E}[f(x)]&=\int f(x) \frac{p(x)}{\int p(x) d x} d x\\&=\frac{\int f(x) p(x) d x}{\int p(x) d x}\\&=\frac{\int f(x) \frac{p(x)}{q(x)} q(x) d x}{\int \frac{p(x)}{q(x)} q(x) d x}.\end{aligned}\]

而分子分母可分别得到，下面两式约等于都利用 \(q(x)\) 是均匀分布的假设：

\[\begin{aligned}\int f(x) \frac{p(x)}{q(x)} q(x) d x &\approx \frac{1}{n} \sum_{i=1}^{n} W_{i} f\left(x_{i}\right), \\\int \frac{p(x)}{q(x)} q(x) d x &\approx \frac{1}{n} \sum_{i=1}^{n} W_{i}.\end{aligned}\]

其中 \(W_i=\frac{p(x_i)}{q(x_i)}\) ，则最终可得 \(\mathbb{E}[f(x)]\) :

\[\begin{aligned}\mathbb{E}[f(x)] \approx \sum_{i=1}^{n} w_{i} f\left(x_{i}\right), w_{i}=\frac{W_{i}}{\sum_{i=1}^{n} W_{i}}\end{aligned}\]

多重重要性采样

有的时候, 需要积分的方程中可能包含多个需要积分的部分, 这时候就需要用到多重重要性采样(multiple importance sampling/MIS).

比如现在要求解 \(\int_{}^{} g_1(x)g_2(x)\) 这样的积分时, 两个部分分别对应两个概率密度 \(f_1(x), f_2(x)\) , MIS给出的新的蒙特卡洛估计为:

\[\frac{1}{n_1} \sum_{i=1}^{n_1}{\frac{g_1(X_1)g_2(X_1)\omega_1(X_1)}{f(X_1)}} + \frac{1}{n_2} \sum_{i=1}^{n_2}{\frac{g_1(X_2)g_2(X_2)\omega_2(X_2)}{f(X_2)}}\\\]

\(n_1,n_2\) 分别是两边的采样次数, \(\omega_1, \omega_2\)分别是两个部分对应的权重.

一个常用的权重函数为:

\[\omega_k = \frac{(n_kf_k(x))^2} {\sum_{i}^{}{(n_1f_i(x))^2}}\\\]

在上面有两个部分的情况下得:

\[\omega_1 = \frac{(n_1f_1(x))^2} {(n_1f_1(x))^2 +(n_2f_2(x))^2 }\\ \omega_2 = \frac{(n_2f_2(x))^2} {(n_1f_1(x))^2 +(n_2f_2(x))^2 }\\\] 与拒绝采样一样，重要性采样的效果与提议分布 \(q(x)\)同 \(p(x)\) 的接近程度紧密相关。当 \(p(x)\) 比较复杂时，选择合适的 \(q(x)\) 是非常困难的。