Energy Based Models

本学习笔记用于记录我学习Stanford CS236课程的学习笔记，分享记录，也便于自己实时查看。

引入

生成模型的核心目标是对目标样本的概率分布进行预测。而对于一个概率密度函数 \(P(x)\) ，它只需要满足下面两个条件：

• 非负， \(P(x)\) 在任何一个点都不能小于0，这很显然。
• 积分为1， \(P(x)\) 从负无穷积分到正无穷得是1。

其中对于第二点，如果 \(P(x)\) 的不是1，是 \(Z\) ，我们进行一下归一化，除一下 \(Z\) 就是1啦。反正至少得是有限的。那么如果我们有一个函数 \(f(x)\) ，我们只需要对其进行变换，满足上面两个特点，便能将其转化为一个概率密度函数。

首先可以让 \(f(x)\) 变为非负的 \(g(x)\) ，比如

• \(g(x) = f(x)^2\)
• \(g(x) = e^{f(x)}\)
• \(g(x) = log(1 + f(x)^2)\)
• ......

可以看到这样的选择有很多，然后接下来便是归一化了，只需要

\[P(x) = \frac{g(x)}{\int g(x)dx} = \frac{g(x)}{Z}\]

那么所谓的Energy Based Model 呢，其实很简单，我们就是假设这个函数 \(g(x) = e^{f(x)}\) 。

这个时候，下面那个体积volume呢，也叫做partition function。

为啥要 \(exp()\) 呢？因为希望在算概率的时候取log，和这个 $ e x p ( ) $ 很多时候能够抵消。而且也和统计物理（虽然笔者并没有研究过统计物理）也有一些联系，这也是energy名字的最初由来。

基本定义

对数据的概率分布进行描述时，这些概率分布都可以写成基于能量函数的形式(energy funciton)， \(f(\mathbf x )\) 。对于连续变量，每个数据点对应一个概率密度函数值，对应一个能量值，如此概率分布即可写成如下玻尔兹曼分布的形式，也叫作吉布斯分布(Boltzmann/Gibbs distribution)：

• \(p(\mathbf x )=\frac{e^{f(\mathbf x)}}{Z}\)
• \(Z\) 为概率归一化的分母，也称为配分函数(partition function)， \(Z=\int e^{f(\mathbf x)} dx\)

由以上公式可知，概率值较高的位置对应着能力较低的点。举一个简单的例子看一下，将高斯分布以能量函数的形式表示：

\[f(x;\mu,\sigma^2)=-\frac{1}{2\sigma^2}(x-\mu)^2\]

\[p(x)=\frac{e^{f(\mathbf x)}}{\int e^{f(\mathbf x)}dx}=\frac{e^{-\frac{1}{2\sigma^2}(x-\mu)^2}}{\sqrt {2\pi \sigma^2}}\]

部分应用

分类任务

一般来说，这个partition funtion是不能算的，除非是限制为一些可以积分的函数，得到闭式解，但那样表达力又太弱了。而在实际中，我们的 \(f(x)\) 一般是用神经网络进行模拟的，所以很难求出这个积分（你也可以遍历所有的情况，但这对于训练或者推理都是无法接受的）。

有时候呢，除非是要算出具体的概率，我们不需要管这个partition function，反正就是知道它是个常数。

比如我们想知道 \(p(a)\) 和 \(p(b)\) 哪个概率大，就不用去知道绝对的值，只需要知道相对大小就可以啦。这就可以用在分类任务里了。

比如对于图像识别的任务，我只需要知道一个物体是更有可能像猫还是更有可能像狗，而不一定要知道他们的具体概率。

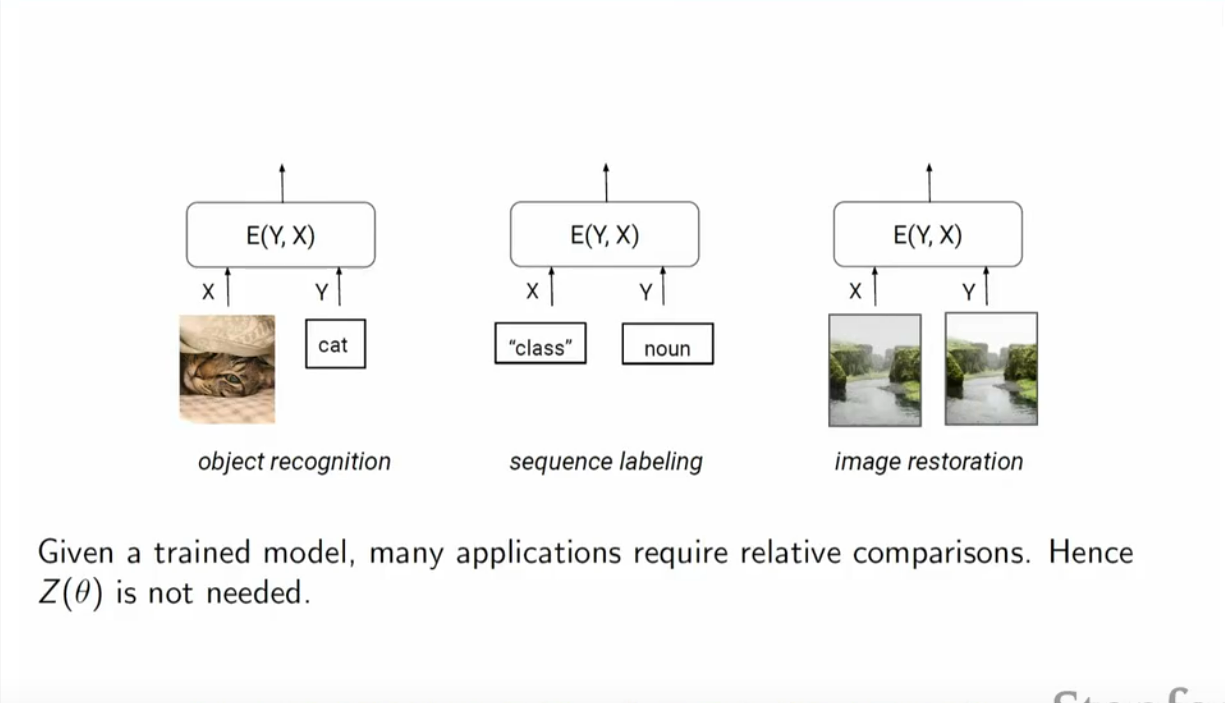
课程中还列举了一个Ising model 的例子，也很直观，不赘述了：

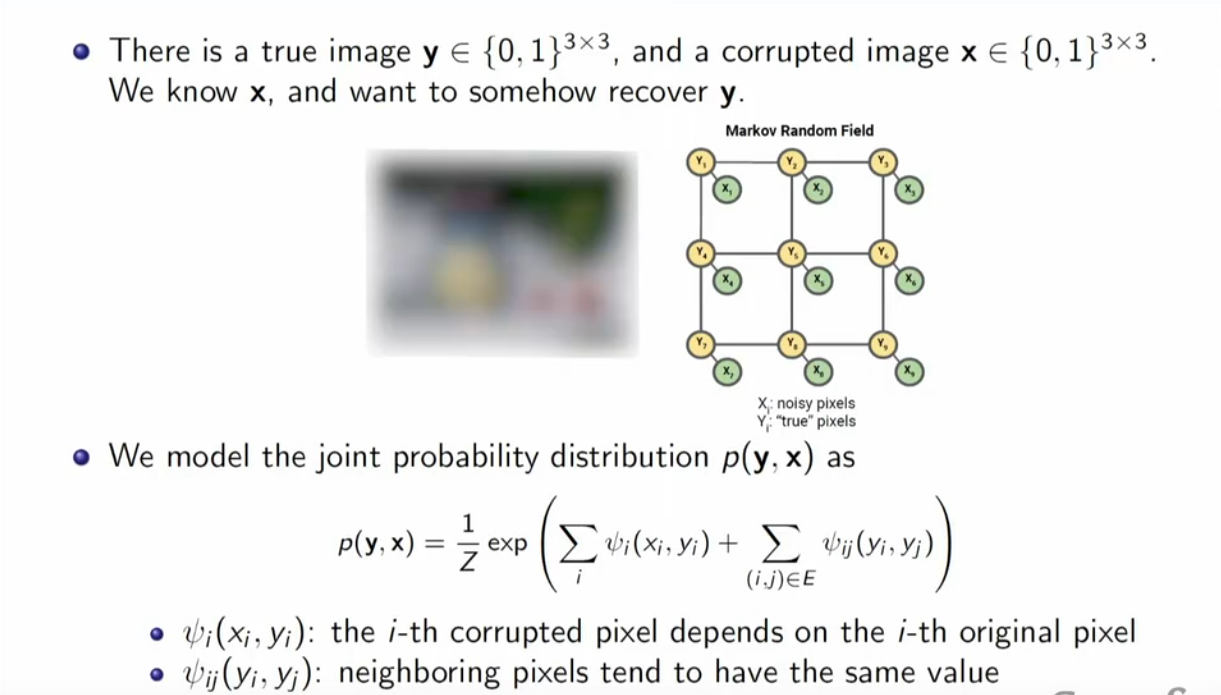
组合专家系统

通过EBMs，可以把多个专家模型混合起来，用乘法。在对模型采样的时候，就会具有多个生成模型的所有性质，比如又是女人又是年轻又是美貌，就不会生成一个年迈的男人。

受限玻尔兹曼机也是基于能量模型，能量形式如下:
\[f(\mathbf x;\theta)=exp(\mathbf x ^T\mathbf{Wx}+\mathbf{b}^T\mathbf{x} + \mathbf{c}^T\mathbf{z})\]

其它就不赘述了。

训练

损失函数（训练目标）

那么如何优化这个模型，直接想法肯定是极大似然估计

\[L = \ log (\frac{exp({f_\theta(x_{train})})}{Z(\theta)}) = f_\theta(x_{train}) - log(Z(\theta))\]

这里有个小问题，直接最大化分子并不能解决问题，因为分母是分子的积分，如果只顾着最大化分子的话，可能分母也跟着变大，那最后这整个分数就可能不变甚至变小！但是积分我们又计算不出来怎么办？蒙特卡洛估计便可以派上用场了，我们对 \(L\) 求一下梯度：

\[ \begin{align*} \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \nabla_{\theta} \log Z(\theta) &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \frac{\nabla_{\theta} Z(\theta)}{Z(\theta)} \\ &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \frac{1}{Z(\theta)} \int \nabla_{\theta} \exp \{ f_{\theta}(x) \} dx \\ &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \frac{1}{Z(\theta)} \int \exp \{ f_{\theta}(x) \} \nabla_{\theta} f_{\theta}(x) dx \\ &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \int \frac{\exp \{ f_{\theta}(x) \}}{Z(\theta)} \nabla_{\theta} f_{\theta}(x) dx \\ &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \mathbb{E}_{x_{\text{sample}}} [\nabla_{\theta} f_{\theta}(x_{\text{sample}})] \\ &= \nabla_{\theta} f_{\theta}(x_{\text{train}}) - \nabla_{\theta} f_{\theta}(x_{\text{sample}}) \end{align*} \]

其中 \(x_{sample} \sim exp(f_\theta(x_{sample}))/Z_\theta\)

最后一步代表在训练过程中，我们只取一个样本作为期望的估计值。

其实主观上也很好理解，其实就是对比了训练集和从模型中的采样，让训练集中数据的概率比随便采样出来的概率大。

我们对上面公式取个负，就是损失函数了。

如何采样

那么问题来了，我们怎么从这个能量模型中采样呢？你看看上面能量模型的式子，你只知道x比y概率大还是概率小，但你不知道x或者y的准确概率。

这时候，MCMC马尔科夫链蒙特卡罗就出场啦。

这是课程对于MCMC的叙述，没明白的可以复习一下，其实就是MH算法：

课程中没强调这个noise是对称的，就是 \(x\) 到 \(x'\) 的概率等于 \(x'\) 到 \(x\) 的概率。这时候上图中的关于 \(q\) 的分数就等于一了。那就是说，如果 \(f(x’)\) 的值大于当前值，那就无脑接受就好啦（2.1步）。如果没有大于，那就算一下比例咯（2.2步）。所以课程中的这个算法就是MH算法。

MH算法很美妙，但太慢啦。那怎么办呢？我们可以用郎之万Langevin 动力学来帮助MH算法，让随机游走朝着概率更高的地方走。 这就是 Metropolis-adjusted Langevin algorithm。

最后总结一下，先用MH算法抽样，用这些抽样放到contrasive divergence 算法里训练能量模型的参数，来极大似然

Score Matching

上面我们用MH算法给出了一个训练和推理的方法，但缺点很明显，就是收敛的太慢了，随着维度的增加，收敛速度指数级别下降。虽然用了郎之万Langevin 动力学来进行提速，但每次梯度一更新之后，分布就变了。所以对于contrasive divergence 的每一步来说，MCMC都要从头开始采样直到收敛。（MCMC采样不是一开始就能用的，要丢弃前n个样本，叫做burn in）

拿能否训练时候不用sampling呢？

score function

先看一下什么叫score function

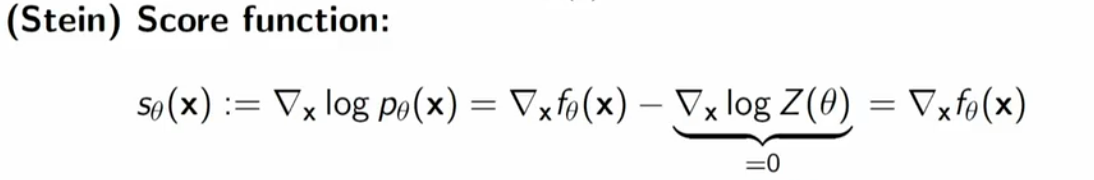
就是指向高概率方向的梯度。一个观察是，这个梯度和分母，就是partition function无关。至于为什么叫做score fuction，那是因为我们一般把 \(f_\theta(x)\) 对输入x的梯度称为score。

score matching

在之前的MCMC采样方法训练中，当我们有了一个准确的能量模型后，我们从数据分布里采样就转换成了根据训练好的能量模型的score, 来进行MCMC采样。那么为什么不能换个思路，直接将能量模型建模成score，即用一个神经网络来拟合score! 这个方法就叫score-matching!

如上所示，我们的目标依旧是用score matching 来减小这两个分布的区别。难点在于，对于真实分布Pdata怎么求导呢？先看看一维的情况：

\[ \begin{align*} \frac{1}{2} \mathbb{E}_{x \sim p_{\text{data}}} \left[ (\nabla_x \log p_{\text{data}}(x) - \nabla_x \log p_{\theta}(x))^2 \right] &= \frac{1}{2} \int p_{\text{data}}(x) \left[ (\nabla_x \log p_{\text{data}}(x) - \nabla_x \log p_{\theta}(x))^2 \right] dx &\\ &= \frac{1}{2} \int p_{\text{data}}(x) (\nabla_x \log p_{\text{data}}(x))^2 dx + \frac{1}{2} \int p_{\text{data}}(x) (\nabla_x \log p_{\theta}(x))^2 dx - \int p_{\text{data}}(x) \nabla_x \log p_{\text{data}}(x) \nabla_x \log p_{\theta}(x) dx & \end{align*} \]

其中第一项是常数，我们不用管，第二项也只涉及到 \(p_\theta\) (积分的 \(p_{data}\) 直接通过在训练集抽样即可)，第三项比较棘手，涉及到 \(\nabla_x \log p_{\text{data}}(x)\) ，这个我们没法直接求出。

但是我们可以通过分布积分来进行化简：

\[ \begin{align*} -\int p_{\text{data}}(x) \nabla_x \log p_{\text{data}}(x) \nabla_x \log p_{\theta}(x) dx &= - \int p_{\text{data}}(x) \frac{1}{p_{\text{data}}(x)} \nabla_x p_{\text{data}}(x) \nabla_x \log p_{\theta}(x) dx \\ &= - p_{\text{data}}(x) \nabla_x \log p_{\theta}(x) \Big|_{x = -\infty}^{x = \infty} + \int p_{\text{data}}(x) \nabla_x^2 \log p_{\theta}(x) dx \\ &= \int p_{\text{data}}(x) \nabla_x^2 \log p_{\theta}(x) dx \end{align*} \]

其中我们认为 \(p_{\text{data}}(x) \nabla_x \log p_{\theta}(x) \Big|_{x = -\infty}^{x = \infty} = 0\) ，因为我们假定无穷远处的 \(p_{data}\) 为0。

对于多维与一维类似，区别就是我们分部积分得到的结果是 \(log(p_\theta(x))\) 的Hessian的迹，最终我们得到的形式如下：

我们通过分部积分把对 \(P_{data}\) 的梯度项给搞没了，就不用像之前那样费劲的去MCMC了。不过缺点是这个Hessian矩阵算起来很麻烦。

Noise contrastive estimation

把NCE用在Energy Based Model其实思想也很简单，我们在GANs中提到，对于一个真实样本和模型样本进行分类的最佳判别器是，对给定 \(x\) 的判定为真实样本的概率为\(\frac{P_{data}(x)}{P_{data}(x) + P_n(x)}\)。

所以NCE的想法就是我去用生成器组成一个判别器，这个生成器输出概率为 \(P_{\theta^*}(x)\) ，而判别器的输出则是 \(\frac{P_{\theta^*}(x)}{P_{\theta^*}(x) + P_n(x)}\) ，这样当判别器训练成为最佳判别器时， \(P_{\theta^*}(x)\) 就等于 $P_{data}(x) $ 。

注意，这里的 \(P_n\) 的概率是我们给定一个特定噪声分布进行采样的概率，所以很好获得。也就是说在NCE中，非真实样本的概率分布是事先指定的，而不是模型学习得到的。

但是，依旧会到那个问题， \(P_{\theta^*}(x) = \frac{exp(f_{\theta^*}(x))}{Z_{\theta*}}\) ，我的分母怎么处理呢？此时我们可以把 \(Z\) 也作为一个参数进行训练。假如我们能够得到最佳判别器，由于 \(\frac{exp(f_{\theta^*}(x))}{Z^{*}} = P_{data}\) ，所以 \(Z\) 也就肯定是最佳的分区函数了。

把这个形式带入我们二分类的目标函数（与GANs相同，这里不赘述了）：

当然，对于这个 \(p_n\) ，它对于训练效果有很显著的影响，毕竟区分图片和一堆噪声可不用很强的判别能力。所以后面也有对这个的改进工作，具体也就是类似GANs一样，再加一个生成器：

当时，这样就会训练得到两个生成模型了，具体推理阶段都可以使用。

注意，能量模型作为生成模型的一种，建模的是 \(P(x)\) ,主要功能是从 \(P(x)\) 里面采样。上面说的score matching是在训练的时候不用从中采样，加快训练的脚步，但是真正使用的时候还是得有MCMC。NCE因为显式的训练了partition function \(Z\) ，也许可以不用MCMC（但笔者感觉也没有比较好的直接采样方法，个人觉得还是需要靠MCMC，如果读者有好的想法也可以指正我）。