Score Based Models

本学习笔记用于记录我学习Stanford CS236课程的学习笔记，分享记录，也便于自己实时查看。

引入

Score function

上一次我们学习了Energy Based Model。其核心做法是对一个数据集\({x_{1}, x_{2}, ..., x_{N}}\)，我们把数据的概率分布\(p(x)\)建模为：

\[p_{\theta}(\mathbf{x}) = \frac{e^{-f_{\theta}(\mathbf{x})}}{Z_{\theta}}\]

这里\(f_{\theta}(\mathbf{x})\in \mathbb{R}\)。\(Z_{\theta}\)是归一化项保证\(p_{\theta}(\mathbf{x})\)是概率。\(\theta\)是他们的参数。
我们一般可以通过最大似然估计的方式来训练参数\(\theta\)，

\[\max_{\theta}\sum\limits_{i=1}^{N}\log_{\theta}(\mathbf{x}_{i})\]

但是因为

\[\log p_{\theta}(\mathbf{x}) = -f_{\theta}(\mathbf{x}) - \log Z_{\theta}\]

\(Z_{\theta}\)是intractable的，我们无法求出\(\log p_{\theta}(\mathbf{x})\)，自然也就无法优化参数\(\theta\)。

为了解决归一化项无法计算的问题，我们引入score function。 score function的定义为\(\nabla _{\mathbf{x}}\log p(\mathbf{x})\)

所以我们可以发现，score function是与\(Z _{\theta}\)无关的：

\[\mathbf{s}_{\theta}(\mathbf{x}) = \nabla_{\mathbf{x}}\log(\mathbf{x}_{\theta}) = -\nabla_{\mathbf{x}}f_{\theta}(\mathbf{x}) - \nabla_{\mathbf{x}}\log Z_{\theta} = -\nabla_{\mathbf{x}}f _{\theta}(\mathbf{x})\]

Score Based Model

Score matching

现在我们想要训练一个网络来估计出真实的score function。自然地，我们可以最小化真实的score function和网络输出的MSE：

\[\mathcal{L} =\frac{1}{2} \mathbb{E}_{p(\mathbf{x})}[||\nabla_{\mathbf{x}}\log p(\mathbf{x}) - \mathbf{s} _{\theta}(\mathbf{x})||^{2}]\]

但是这样的一个loss我们是算不出来的，因为我们并不知道真实的\(p(\mathbf{x})\)是什么。而score matching方法就可以让我们在不知道真实的\(p(\mathbf{x})\)的情况下最小化这个loss。Score matching的推导如下：
我们把上面loss的期望写开，二次项打开，可以得到

\[\begin{align*}\mathcal{L} =& \frac{1}{2}\mathbb{E}_{p(\mathbf{x})}[||\nabla _{\mathbf{x}}\log p(\mathbf{x}) - \mathbf{s} _{\theta}(\mathbf{x})||^{2}]\\=& \frac{1}{2}\int p(\mathbf{x}) [||\nabla _{\mathbf{x}}\log p(\mathbf{x})||^{2} + ||\mathbf{s} _{\theta}(\mathbf{x})||^{2} - 2(\nabla _{\mathbf{x}}\log p(\mathbf{x}))^{T}\mathbf{s} _{\theta}(\mathbf{x})] d \mathbf{x}\end{align*}\]

第一项对于\(\theta\)来说是常数可以忽略。
第二项为

\[\int p(\mathbf{x}) ||\mathbf{s} _{\theta}(\mathbf{x})||^{2} d \mathbf{x}\]

对于第三项，若\(\mathbf{x}\)的维度为\(N\)：

\[ \begin{align*}& -2\int p(\mathbf{x}) (\nabla _{\mathbf{x}}\log p(\mathbf{x}))^{T}\mathbf{s} _{\theta}(\mathbf{x}) d \mathbf{x}\\ =& -2 \int p(\mathbf{x}) \sum\limits_{i=1}^{N}\frac{\partial \log p(\mathbf{x})}{\partial \mathbf{x}_{i}}\mathbf{s}_{\theta i}(\mathbf{x}) d \mathbf{x}\\ =& -2 \sum\limits_{i=1}^{N} \int p(\mathbf{x}) \frac{1}{p(\mathbf{x})} \frac{\partial p(\mathbf{x})}{\partial \mathbf{x}_{i}}\mathbf{s}_{\theta i}(\mathbf{x}) d \mathbf{x}\\ =& -2 \sum\limits_{i=1}^{N} \int \frac{\partial p(\mathbf{x})}{\partial \mathbf{x}_{i}}\mathbf{s}_{\theta i}(\mathbf{x}) d \mathbf{x}\\ =& 2 \sum\limits_{i=1}^{N} - \int \frac{\partial p(\mathbf{x})\mathbf{s}_{\theta i}(\mathbf{x})}{\partial \mathbf{x}_{i}} d \mathbf{x} + \int p(\mathbf{x}) \frac{\partial \mathbf{s}_{\theta i}(\mathbf{x})}{\partial \mathbf{x}_{i}} d \mathbf{x}\\ =& 2 \sum\limits_{i=1}^{N} - \int p(\mathbf{x})\mathbf{s}_{\theta i}(\mathbf{x})\bigg\rvert^{\infty}_{-\infty} d \mathbf{x_{/i}} + \int p(\mathbf{x}) \frac{\partial \mathbf{s}_{\theta i}(\mathbf{x})}{\partial \mathbf{x}_{i}} d \mathbf{x}\\ =& 2 \sum\limits_{i=1}^{N} \int p(\mathbf{x}) \frac{\partial \mathbf{s}_{\theta i}(\mathbf{x})}{\partial \mathbf{x}_{i}} d \mathbf{x}\\ =& 2\int p(\mathbf{x}) \sum\limits_{i=1}^{N} \frac{\partial \mathbf{s}_{\theta i}(\mathbf{x})}{\partial \mathbf{x}_{i}} d \mathbf{x}\\ =& 2\int p(\mathbf{x}) \text{tr}(\nabla _{\mathbf{x}}\mathbf{s}_{\theta}(\mathbf{x})) d \mathbf{x}\end{align*} \]

所以最后的loss是第二和第三项的和：

\[ \begin{align*} \mathcal{L} &=\frac{1}{2} \int p(\mathbf{x}) ||\mathbf{s} _{\theta}(\mathbf{x})||^{2} d \mathbf{x} + \int p(\mathbf{x}) \text{tr}(\nabla _{\mathbf{x}}\mathbf{s}_{\theta}(\mathbf{x})) d \mathbf{x}\\\\ &= \mathbb{E}_{p(\mathbf{x})}[\frac{1}{2}||\mathbf{s} _{\theta}(\mathbf{x})||^{2} + \text{tr}(\nabla _{\mathbf{x}}\mathbf{s}_{\theta}(\mathbf{x}))]\end{align*} \]

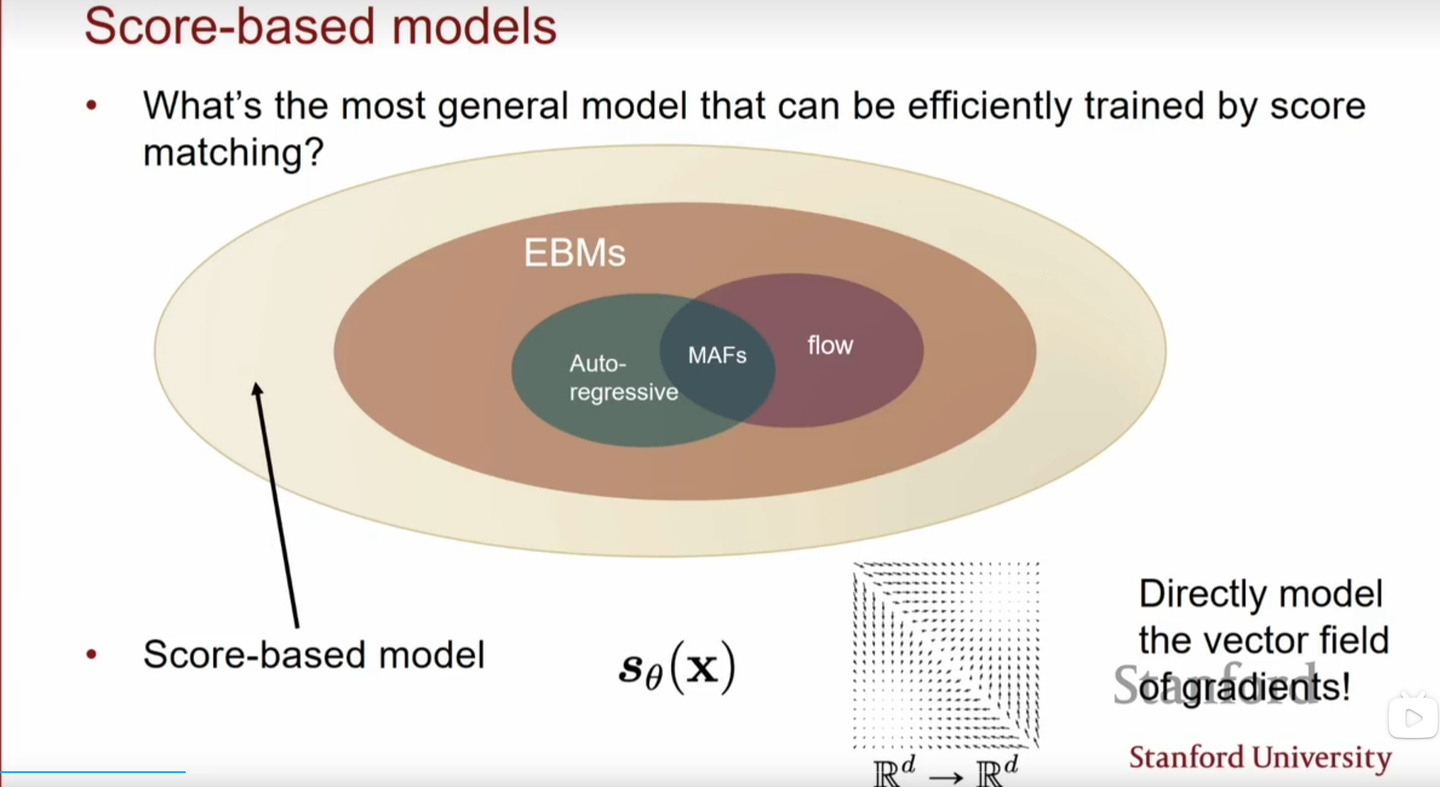
当然，这个推导虽然是从能量模型引入的，但并不局限于能量模型，事实上，他是一个更大的模型家族。

Score Matching Langevin Dynamics (SMLD)

现在我们已经通过神经网络学习到了数据分布的score function，那么如何用score function从这个数据分布中得到样本呢？答案就是朗之万动力学采样(Langevin Dynamics):

\[ \mathbf{x}_{i+1} = \mathbf{x}_{i} + \epsilon \nabla_{\mathbf{x}}\log p(\mathbf{x}) + \sqrt{2 \epsilon}\mathbf{z}_{i}, \quad \mathbf{z} _{i} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), \quad i=0,1,\cdots K\ \]

这里的采样是一个迭代的过程。\(\epsilon\)是一个很小的量。\(\mathbf{x}_{0}\)随机初始，通过上面的迭代式更新。当迭代次数\(K\)足够大的时候，\(\mathbf{x}\)就收敛于该分布的一个样本。

上图的具体解释我就不再赘述了。

这样我们其实就得到了一个生成模型。我们可以先训练一个网络用来估计score function，然后用Langevin Dynamics和网络估计的score function采样，就可以得到原分布的样本。因为整个方法由score matching和Langevin Dynamics两部分组成，所以叫SMLD。

训练

说完了损失函数和采样过程，那么对这个模型我们怎么训练呢？相信敏锐的读者已经注意到了，我们损失函数：

\[ \begin{align*} \mathcal{L} &= \mathbb{E}_{p(\mathbf{x})}[\frac{1}{2}||\mathbf{s} _{\theta}(\mathbf{x})||^{2} + \text{tr}(\nabla _{\mathbf{x}}\mathbf{s}_{\theta}(\mathbf{x}))]\end{align*} \]

这个第二项并不是很好计算。对于维度为\(N\)的数据，我们计算雅可比矩阵的迹需要进行\(N\)次反向传播，这对于高维度的数据的训练是不能接受的。

对于这个问题，主要有两种解决方法。

Denoising score matching

Denoising score matching的做法就是在 score matching 的基础上，对输入数据加噪。需要注意的是，此时的 score 是对加噪后的数据进行求导，而非原输入数据。score 的方向是(对数)概率密度增长最快的方向，也就是最接近真实数据的方向。
Denoising score matching 的玩法是：在给定输入\(x\)的情况下，将条件分布\(q(\tilde{x}|x)\)建模为高斯分布，其中\(\tilde{x}\)代表加噪后的数据，并且边缘化这个条件分布，以\(p(\tilde{x}) \equiv \int q(\tilde{x}|x)p(x) dx\)来近似原数据分布，因此噪声强度不太大时，我们可以认为加噪后数据的概率分布与原数据的概率分布大致相同。

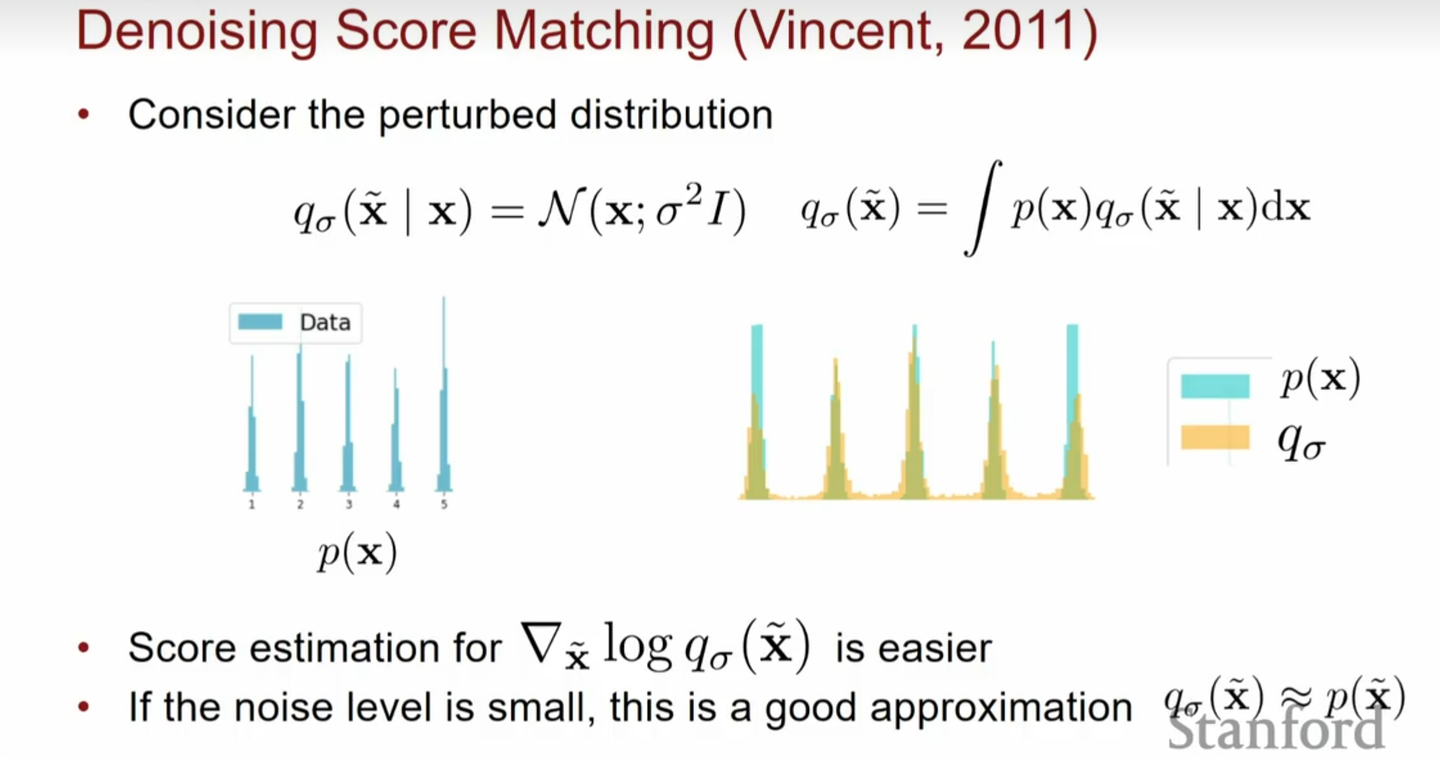
此时，score\(\frac{\partial log(p(\tilde{x}))}{\partial \tilde{x}}\)中由于\(p(x)\)项在求导时与\(\tilde{x}\)无关，可以略去了，具体推导如下：

\[ \begin{align*} \frac{1}{2} \mathbb{E}_{\tilde{x} \sim q_{\sigma}} \left[ \| \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}) - s_{\theta}(\tilde{x}) \|_2^2 \right] &= \frac{1}{2} \int q_{\sigma}(\tilde{x}) \| \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}) - s_{\theta}(\tilde{x}) \|_2^2 d\tilde{x} \\ &= \frac{1}{2} \int q_{\sigma}(\tilde{x}) \| \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}) \|_2^2 d\tilde{x} + \frac{1}{2} \int q_{\sigma}(\tilde{x}) \| s_{\theta}(\tilde{x}) \|_2^2 d\tilde{x}- \int q_{\sigma}(\tilde{x}) \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x})^T s_{\theta}(\tilde{x}) d\tilde{x} \end{align*} \] 这里一样的，第一项是常数，第二项只涉及\(s_{\theta}(\tilde{x})\)，我们可以处理，第三项比较棘手。但我们可以类似地用分布积分法进行处理：

\[ \begin{align*} &- \int q_{\sigma}(\tilde{x}) \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x})^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int q_{\sigma}(\tilde{x}) \frac{1}{q_{\sigma}(\tilde{x})} \nabla_{\tilde{x}} q_{\sigma}(\tilde{x})^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int \nabla_{\tilde{x}} q_{\sigma}(\tilde{x})^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int \nabla_{\tilde{x}} \left( \int p_{\text{data}}(x) q_{\sigma}(\tilde{x} | x) dx \right)^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int \left( \int p_{\text{data}}(x) \nabla_{\tilde{x}} q_{\sigma}(\tilde{x} | x) dx \right)^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int \left( \int p_{\text{data}}(x) q_{\sigma}(\tilde{x} | x) \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x} | x) dx \right)^T s_{\theta}(\tilde{x}) d\tilde{x} \\ &= - \int \int p_{\text{data}}(x) q_{\sigma}(\tilde{x} | x) \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x} | x)^Ts_{\theta}(\tilde{x}) dx \ d\tilde{x} \end{align*} \] 这里我们\(q(\tilde{x}|x)\)是已知的，也就可以计算了。

OK，让我们代入原式之中：

\[ \begin{align*} &\frac{1}{2} \mathbb{E}_{\tilde{\mathbf{x}} \sim q_{\sigma}} \left[ \|\nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}}) - s_{\theta} (\tilde{\mathbf{x}}) \|_2^2 \right] \\ &= \text{const.} + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim q_{\sigma}} \left[ \| s_{\theta} (\mathbf{x}) \|_2^2 \right] - \int q_{\sigma} (\tilde{\mathbf{x}}) \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}})^{\top} s_{\theta} (\tilde{\mathbf{x}}) d\tilde{\mathbf{x}} \\ &= \text{const.} + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim q_{\sigma}} \left[ \| s_{\theta} (\tilde{\mathbf{x}}) \|_2^2 \right] - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x}), \tilde{\mathbf{x}} \sim q_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})} \left[ \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}}|\mathbf{x})^{\top} s_{\theta} (\tilde{\mathbf{x}}) \right] \\ &= \text{const.} + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x}), \tilde{\mathbf{x}} \sim q_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})} \left[ \| s_{\theta} (\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}}|\mathbf{x}) \|_2^2 \right] - \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x}), \tilde{\mathbf{x}} \sim q_{\sigma}(\tilde{\mathbf{x}})} \left[ \| \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}}) \|_2^2 \right] \\ &= \text{const.} + \frac{1}{2} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x}), \tilde{\mathbf{x}} \sim q_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})} \left[ \| s_{\theta} (\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}} \log q_{\sigma} (\tilde{\mathbf{x}}|\mathbf{x}) \|_2^2 \right] + \text{const.} \end{align*} \]

看到没有！这也就是说，score 的方向与所加噪声的方向是相反的。 于是，在 denoising score matching 的体制下，朝着 score 的方向走，其实就是在去噪，在做 denoising。

在实践中，我们可以选择将\(q(\tilde{x}|x)\)建模为\(N(\tilde{x};x;\sigma^2)\)，即均值为原数据\(x\)，方差为预设的\(\sigma^2\)的高斯分布。于是，根据高斯分布的性质，有：

\[\tilde{x}=x + \sigma \epsilon, \epsilon\sim N(0,I)\]

其中，\(\epsilon\)是从标准高斯分布中采样出来的噪声。

接着，在以上化简出的 score 中代入高斯分布的概率密度函数，可以得到 score 为：

\[\frac{\partial log (q(\tilde{x}|x))}{\partial \tilde{x}} = -(\frac{\tilde{x}-x}{\sigma^2})=-\frac{\epsilon}{\sigma}\]

虽然我们对计算进行了大幅度简化，但这也导致了我们估计的是加噪数据的梯度。具体训练流程如下：

Sliced score matching

Sliced score matching的思想是，如果模型预测的梯度与真实梯度相同等价于他们在不同方向下的投影均相同，所以我们引入一个投影向量用于训练。这样我们的目标和最终化简（用分部积分即可）的格式如下：

• goal： \[ \frac{1}{2} \mathbb{E}_{\mathbf{v} \sim p_v} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \left( \mathbf{v}^{\top} \nabla_{\mathbf{x}} \log p_{\text{data}} (\mathbf{x}) - \mathbf{v}^{\top} s_{\theta} (\mathbf{x}) \right)^2 \right] \]
• loss： \[\mathbb{E}_{\mathbf{v} \sim p_v} \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}} \left[ \mathbf{v}^{\top} \nabla_{\mathbf{x}} s_{\theta} (\mathbf{x}) \mathbf{v} + \frac{1}{2} (\mathbf{v}^{\top} s_{\theta} (\mathbf{x}))^2 \right] \]

这样我们便只需要进行一次反向传播了，大大减少了训练需要的计算量，计算图如下：

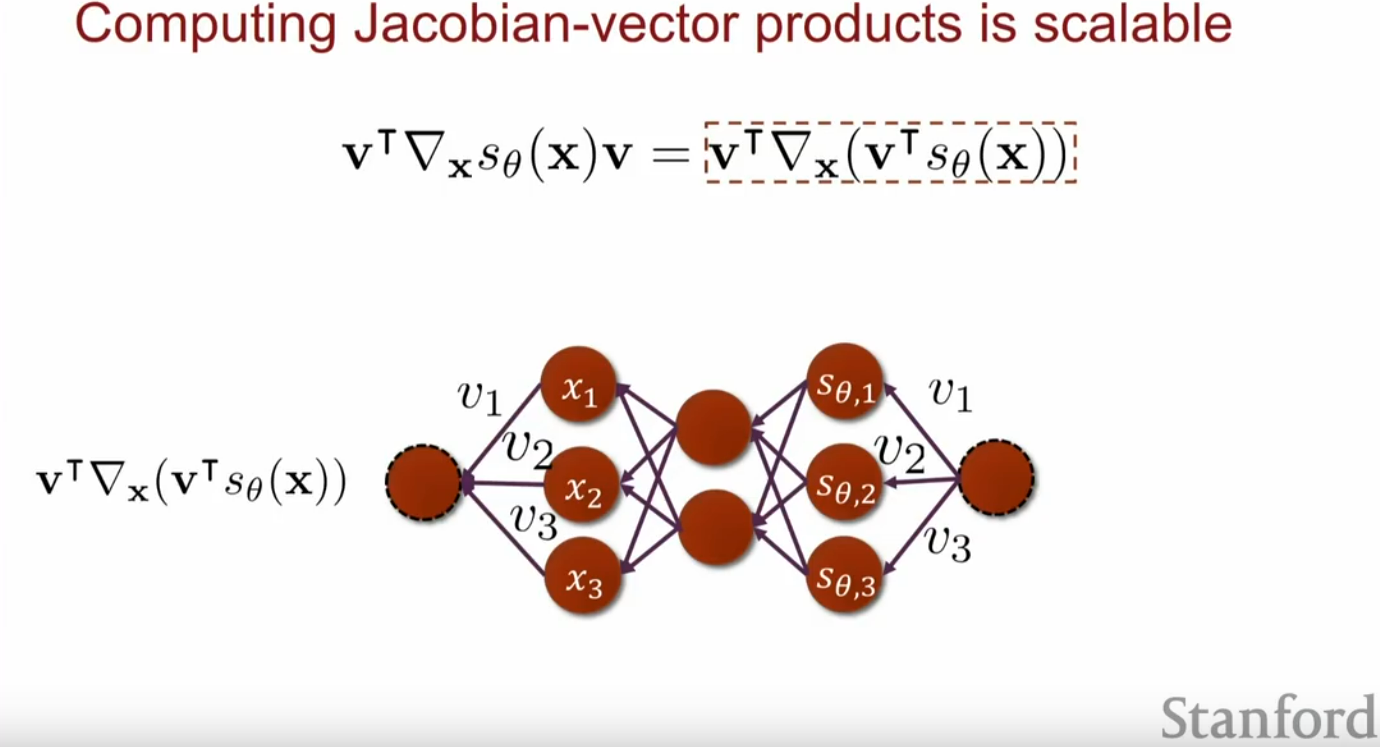
具体训练过程如下：

虽然这种方法的训练计算量会比Denoising score matching大，但它是对真实数据梯度进行的估计

问题

现在我们得到了SMLD生成模型，但实际上这个模型由很大的问题。首先看一下其在实践中的效果：

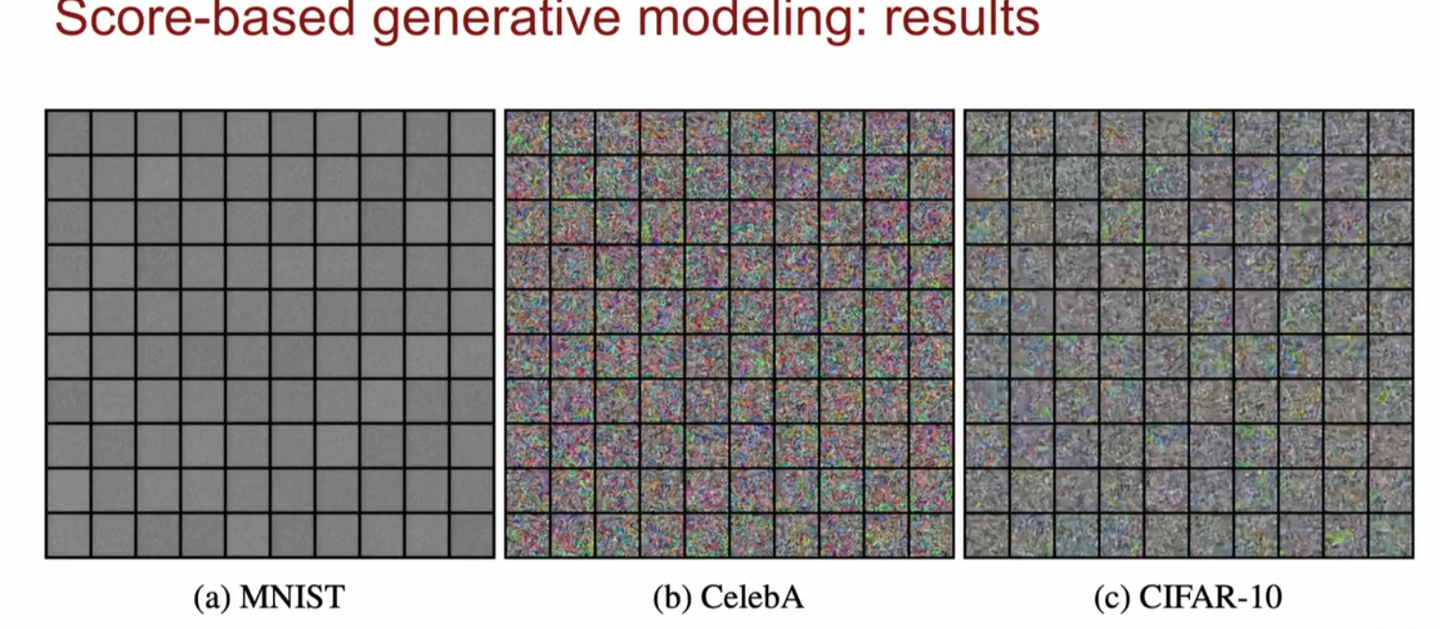
可以看到效果并不好。我们不妨从损失函数来分析一下原因：

\[ \mathcal{L} = \mathbb{E}_{p(\mathbf{x})}[||\nabla_{\mathbf{x}}\log p(\mathbf{x}) - \mathbf{s}_{\theta}(\mathbf{x})||^{2}] = \int p(\mathbf{x})||\nabla_{\mathbf{x}}\log p(\mathbf{x}) - \mathbf{s} _{\theta}(\mathbf{x})||^{2} d \mathbf{x}\ \]

观察我们用来训练神经网络的损失函数，我们可以发现这个L2项其实是被\(p(\mathbf{x})\)加权了。所以对于低概率的区域，估计出来的score function就很不准确：

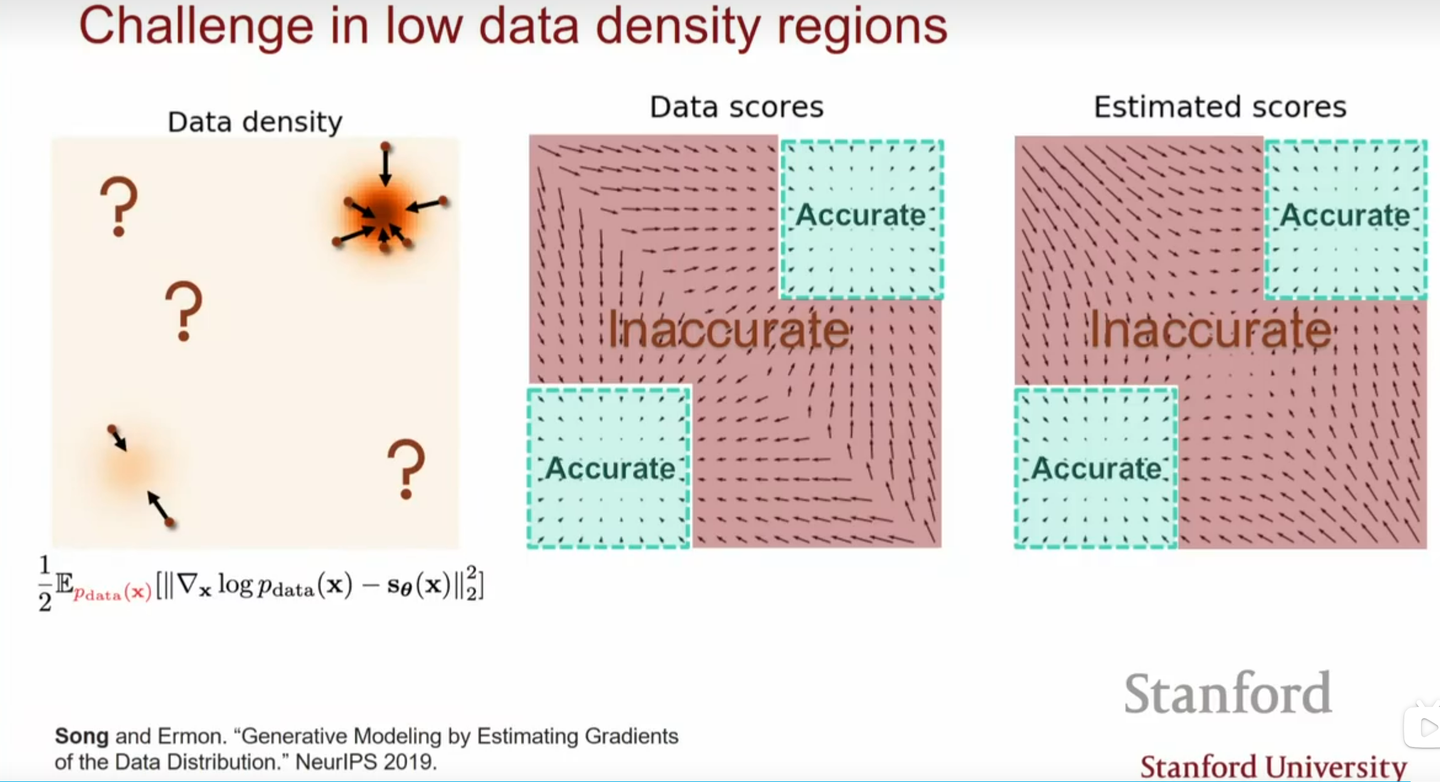
对于上面这张图来说，只有在高概率的红色区域，loss才高，score function可以被准确地估计出来。但如果我们采样的初始点在低概率区域的话，因为估计出的score function不准确，很有可能生成不出真实分布的样本。

此外，在现实中，比如对于图片来说，其往往是分布在一个低维度流型上，也就是大部分空间的概率密度几乎为0，此时我们的梯度定义已经失去了意义：

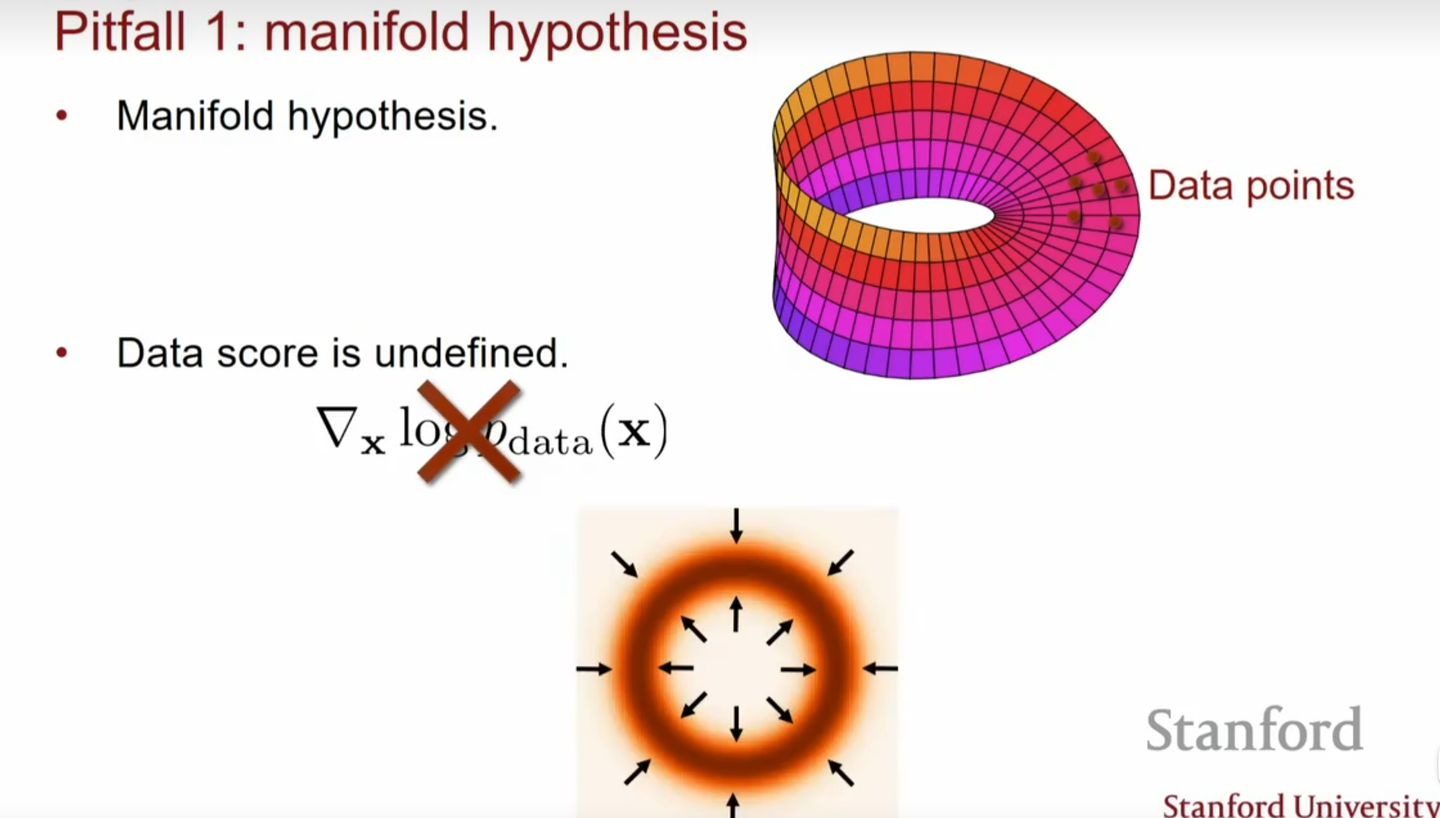
同时，我们通过Langevin Dynamics进行采样并不能很好还原聚点的样本比：

SMLD的改进

那怎么样才能解决上面的问题呢？Denoising score matching给我们给了一定的启发。
其实可以通过给数据增加噪声扰动的方式扩大高概率区域的面积。给原始分布加上高斯噪声，原始分布的方差会变大。这样相当于高概率区域的面积就增大了，更多区域的score function可以被准确地估计出来。

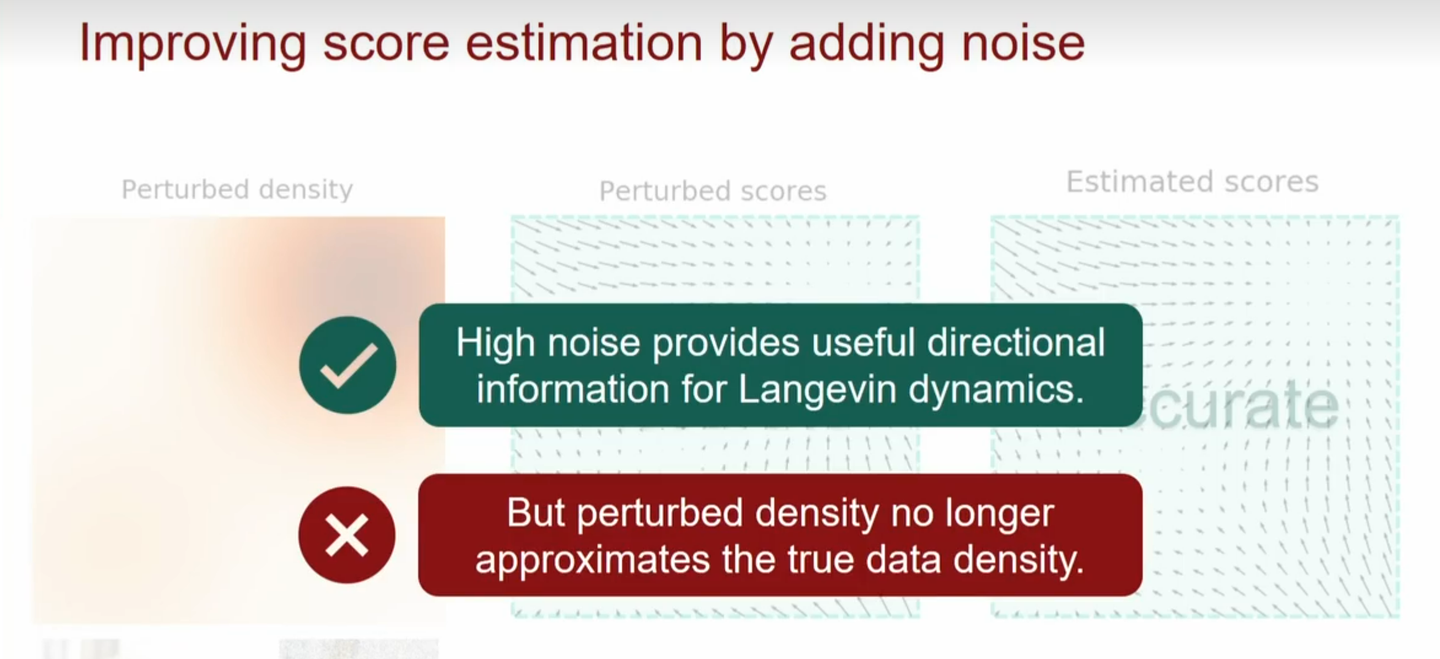
但是噪声扰动的强度如何控制是个问题：

• 强度太小起不到效果，高概率区域的面积还是太小
• 强度太大会破坏数据的原始分布，估计出来的score function就和原分布关系不大了

所以噪声强度越高，高概率区域面积越大，训练得到的梯度越准，但与原始数据的梯度差距也就越大。所以我们不妨加不同程度的噪声，让网络可以学到加了不同噪声的原始分布的score function。这样既保证了原始低概率密度地区能学习到有效的梯度，同时原始高概率密度区的梯度估计是准确的。

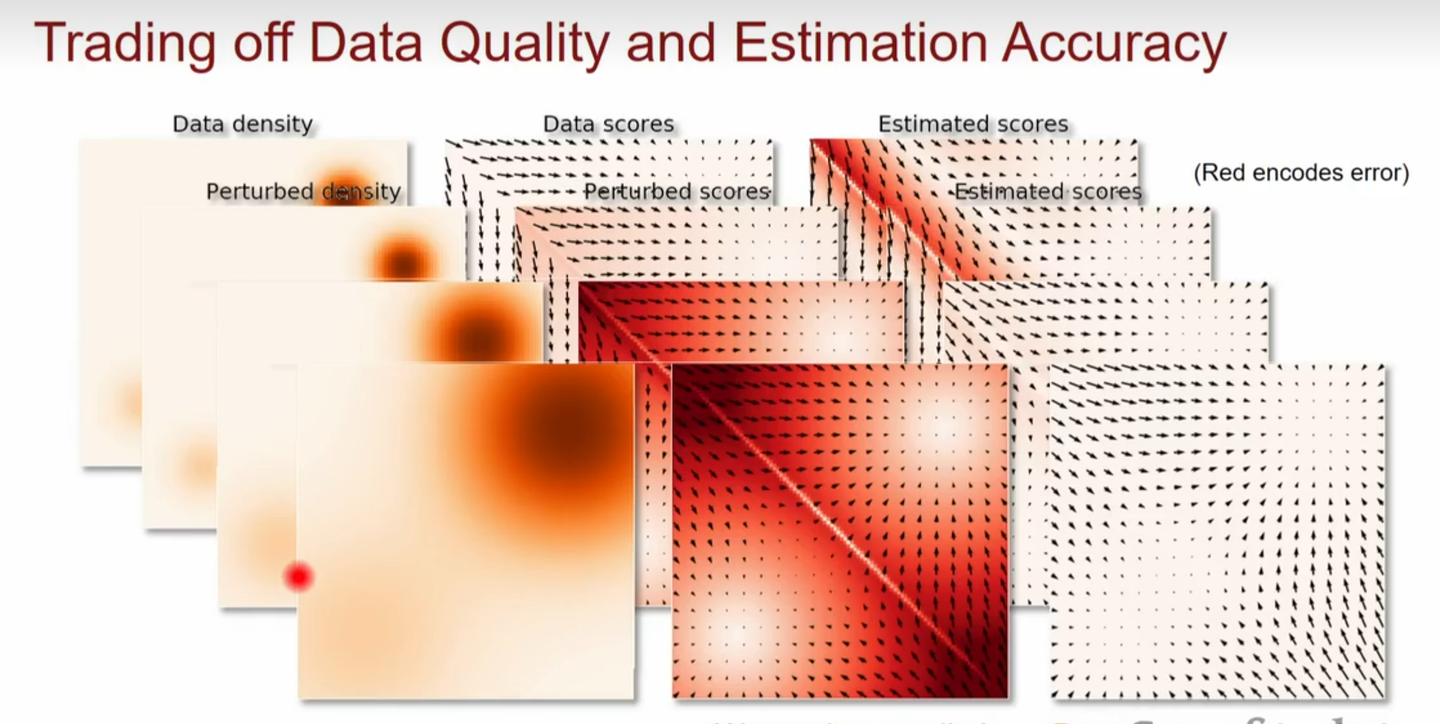
说起来很拗口，其实很好理解。我们定义序列\({\sigma_{1 \sim L}} , \quad \sigma {1} \lt \sigma {2} \lt \cdots \lt \sigma _{L}\)，代表从小到大的噪声强度。这样我们可以定义经过噪声扰动之后的数据样本，服从一个经过噪声扰动之后的分布，

\[ \mathbf{x} + \sigma_{i}\mathbf{z} = \int p(\mathbf{y}) \mathcal{N}(\mathbf{x}|\mathbf{y}, \sigma {i}^{2}\mathbf{I})d \mathbf{y}\ \]

我们用神经网络来估计经过噪声扰动过的分布的score function，并把噪声强度\(\sigma_i\)作为一个输入：

\[ \mathcal{L} = \frac{1}{L}\sum_\limits {i=1}^{L} \lambda (i) \mathbb{E}_{p _{\sigma {i}}(\mathbf{x})}[||\nabla_{\mathbf{x}}\log p_{\sigma _ {i}}(\mathbf{x}) - \mathbf{s} _{\theta}(\mathbf{x, \sigma_i})||^{2}] \]

其中\(\lambda(i)\)是权重，在实践中可以取\(\sigma_{i}^{2}\)

采样方式也要做出相应的变化，我们对于不同的噪声强度\(L, L-1, \cdots, 1\)做Langevin采样，上一个scale的结果作为这一次的初始化。这样我们每一次的初始化都能在梯度估计的有效区域。

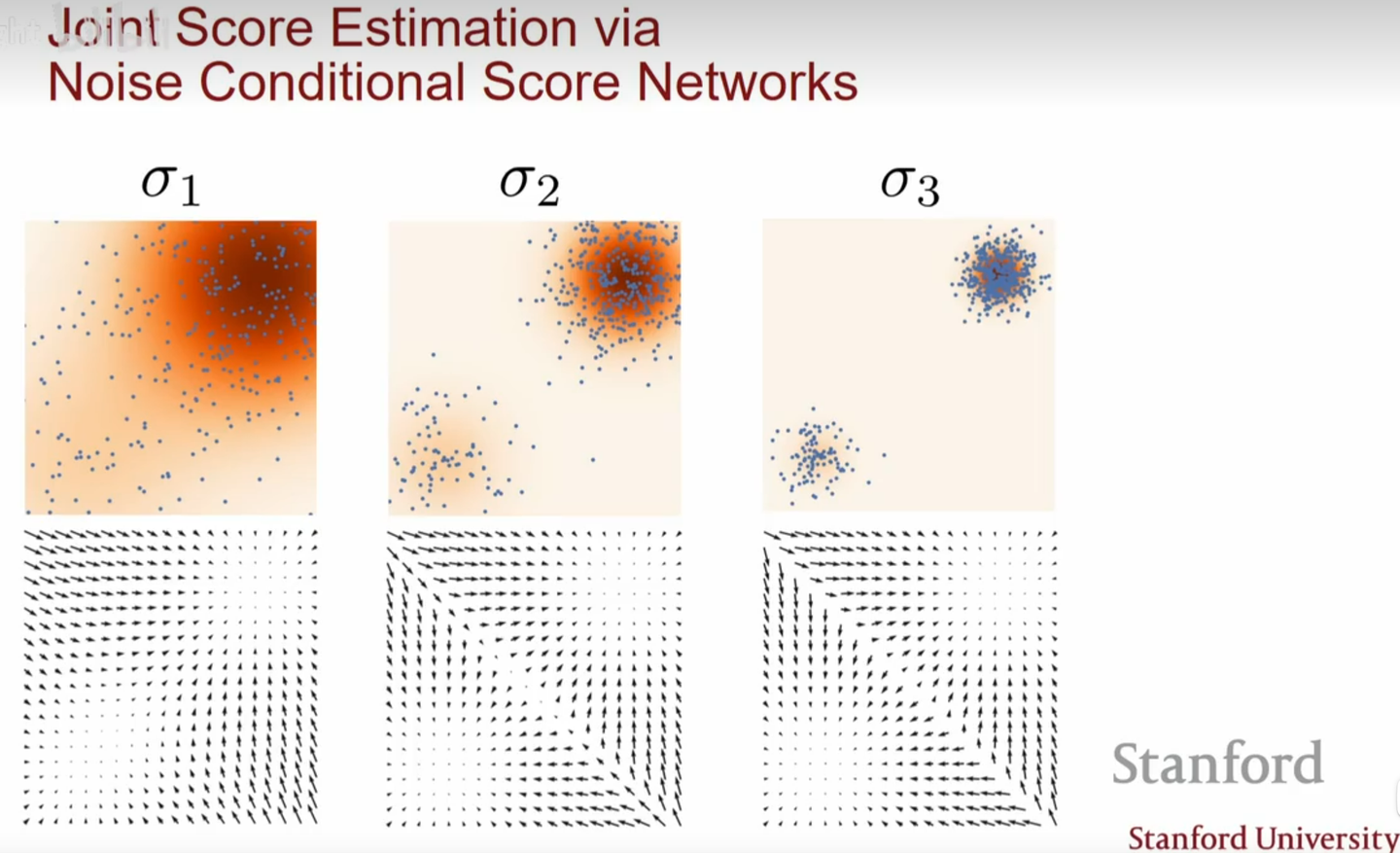
这种采样方式也叫做Annealed Langevin dynamics，具体训练流程如下：

从离散到连续

当我们做Langevin dynamics迭代次数足够多时，我们可以用随机微分方程(Stochastic Differential Equation, SDE)来建模这个采样过程。

\[\mathbf{x}_{i+1} = \mathbf{x}_{i} + \epsilon \nabla_{\mathbf{x}}\log p(\mathbf{x}_i) + \sqrt{2 \epsilon}\mathbf{z}_{i}, \quad i=0,1,\cdots K\]

当\(K\to\infty\)时，我们定义\(\Delta t = \epsilon,\; \Delta t \to 0\)

\[\mathbf{x}_{t+\Delta t} - \mathbf{x}_{t}= \nabla_{\mathbf{x}}\log p(\mathbf{x}_i)\Delta t + \sqrt{2 \Delta t}\mathbf{z}_{i}\]

我们将\(\nabla _{\mathbf{x}}\log p(\mathbf{x}_i)\)和\(\sqrt{2}\)一般化为\(\mathbf{f}(\mathbf{x}, t)\)和\(g(t)\)，这样上面就变成了

\[\mathbf{x} _{t+\Delta t} - \mathbf{x}_{t}= \mathbf{f}(\mathbf{x}, t)\Delta t + g(t) \sqrt{\Delta t}\mathbf{z} _{i}\]

其中

\[\sqrt{\Delta t}\mathbf{z} _{i} \sim \mathcal{N}(\mathbf{0}, \Delta t\mathbf{I})\]

这里可以引入布朗运动，如果我们定义\(\mathbf{w}\)是一个布朗运动，那么

\[ \begin{gather*}\mathbf{w}_{t+\Delta t} = \mathbf{w}_{t} + \mathcal{N}(\mathbf{0}, \Delta t\mathbf{I}),\\ \sqrt{\Delta t}\mathbf{z} _{i} = \mathbf{w}_{t+\Delta t} - \mathbf{w}_{t}.\end{gather*} \]

讲布朗运动带入到上面，得到

\[\mathbf{x}_{t+\Delta t} - \mathbf{x}_{t}= \mathbf{f}(\mathbf{x}, t)\Delta t + g(t)(\mathbf{w}_{t+\Delta t} - \mathbf{w}_{t})\]

当\(\Delta t \to 0\),

\[\text{d}\mathbf{x}= \mathbf{f}(\mathbf{x}, t)\text{d}\mathbf{t} + g(t)\text{d}\mathbf{w}\]

这里\(\mathbf{f}(\mathbf{x}, t)\)叫做drift coefficient,\(g(t)\)代表diffusion coefficient。SDE的解也就代表了数据不断加噪声的过程。

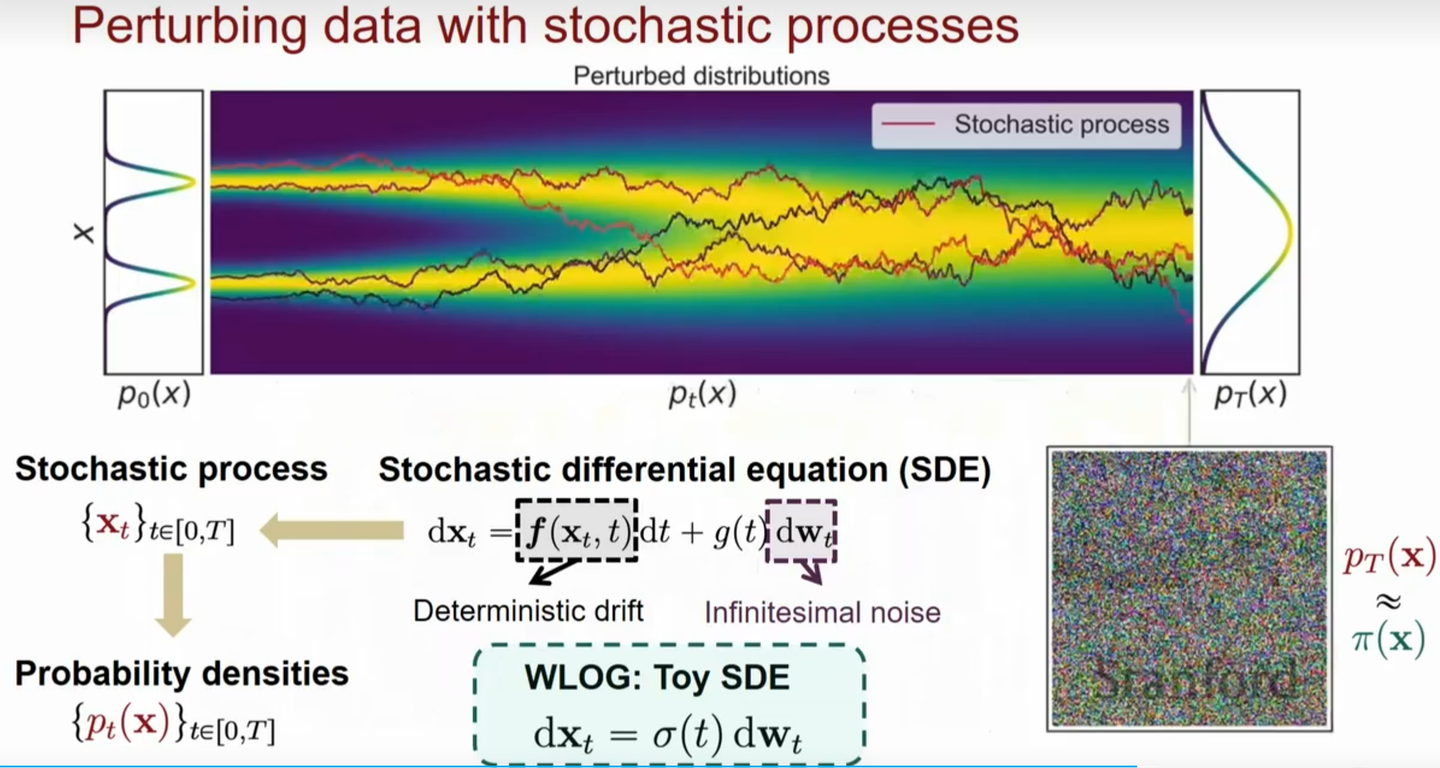
有了正向过程的SDE，我们可以得到

• 反向的SDE

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - g^2(t)\nabla _{\mathbf{x}}\log p(\mathbf{x})]\text{d}\mathbf{t} + g(t)\text{d}\mathbf{w}\]

• 以及score matching的损失函数

\[\mathbb{E}_{t\in \mathcal{U}(0, T)} \mathbb{E}_{p_{t}(\mathbf{x})}[g^2(t)||\nabla_{\mathbf{x}}\log p_t(\mathbf{x}) - \mathbf{s}_{\theta}(\mathbf{x})||^2]\]

可以看到，当我们知道了score后，就能解这个反向的SDE了。

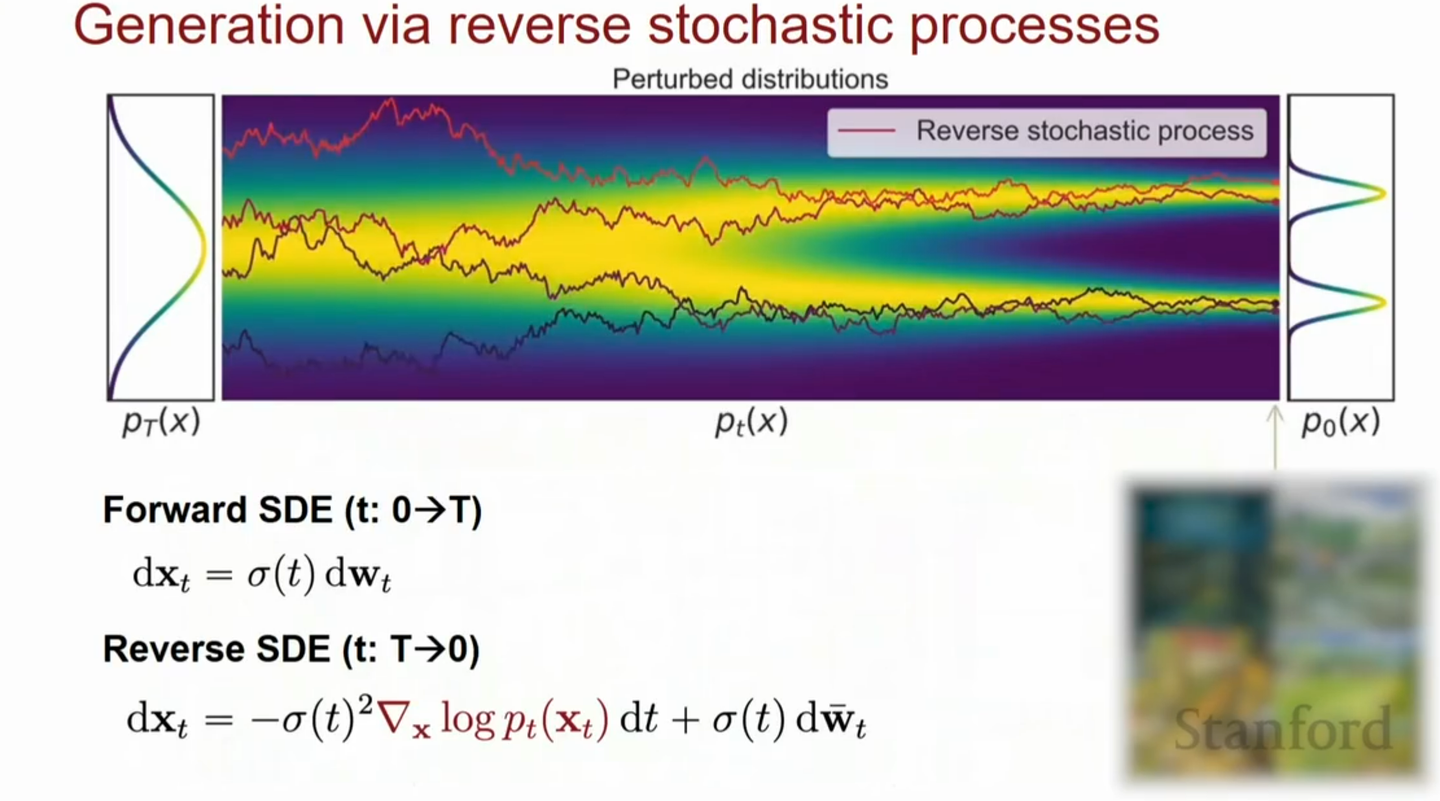
整个基于SDE框架就是：我们在正向过程在图像中加噪声训练神经网络做score matching，估计出score function。然后在反向过程中从高斯噪声通过逆向SDE过程生成出数据分布的样本。

从SDE到ODE

对于一个SDE，

\[\text{d}\mathbf{x}= \mathbf{f}(\mathbf{x}, t)\text{d}\mathbf{t} + g(t)\text{d}\mathbf{w}\]

我们写出它的福克-普朗克方程（Fokker-Planck equation）：

\[ \begin{align*} \nabla _{t}p(\mathbf{x}, t) &= -\nabla _{\mathbf{x}}[\mathbf{f}(\mathbf{x}, t)p(\mathbf{x}, t)] + \frac{1}{2}g^{2}(t)\nabla _{\mathbf{x}}^{2}p(\mathbf{x}, t)\\ &= -\nabla _{\mathbf{x}}[\mathbf{f}(\mathbf{x}, t)p(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}p(\mathbf{x}, t)] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x}}^{2}p(\mathbf{x}, t)\\ &= -\nabla _{\mathbf{x}}[(\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}\log p(\mathbf{x}, t))p(\mathbf{x})] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x}}^{2}p(\mathbf{x}, t)\\\end{align*} \]

现在我们把福克-普朗克方程变成了这样：

\[ \nabla_{t}p(\mathbf{x}, t) = -\nabla_{\mathbf{x}}[(\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}\log p(\mathbf{x}, t))p(\mathbf{x})] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x}}^{2}p(\mathbf{x}, t) \]

其对应的SDE为：

\[ \text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_{\mathbf{x}}\log p_{t}(\mathbf{x})]\text{d}\mathbf{t} + \sigma(t)\text{d}\mathbf{w} \]

因为前后两个SDE是等价的，他们对应的\(p_{t}(\mathbf{x})\)是一样的，意味着我们可以改变第二个SDE的方差\(\sigma(t)\)。当我们取\(\sigma(t)=0\)，可以得到一个常微分方程(Ordinary Differential Equation, ODE),

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g^{2}(t)\nabla_{\mathbf{x}}\log p_{t}(\mathbf{x})]\text{d}\mathbf{t}\]

下图就展示了SDE和ODE解的过程，可以看到ODE的轨迹是确定光滑的，而SDE的轨迹是随机的。这两个过程中的任意边缘分布\({p_{t}(\mathbf{x})}_{t\in[0, T]}\)都是一样的。

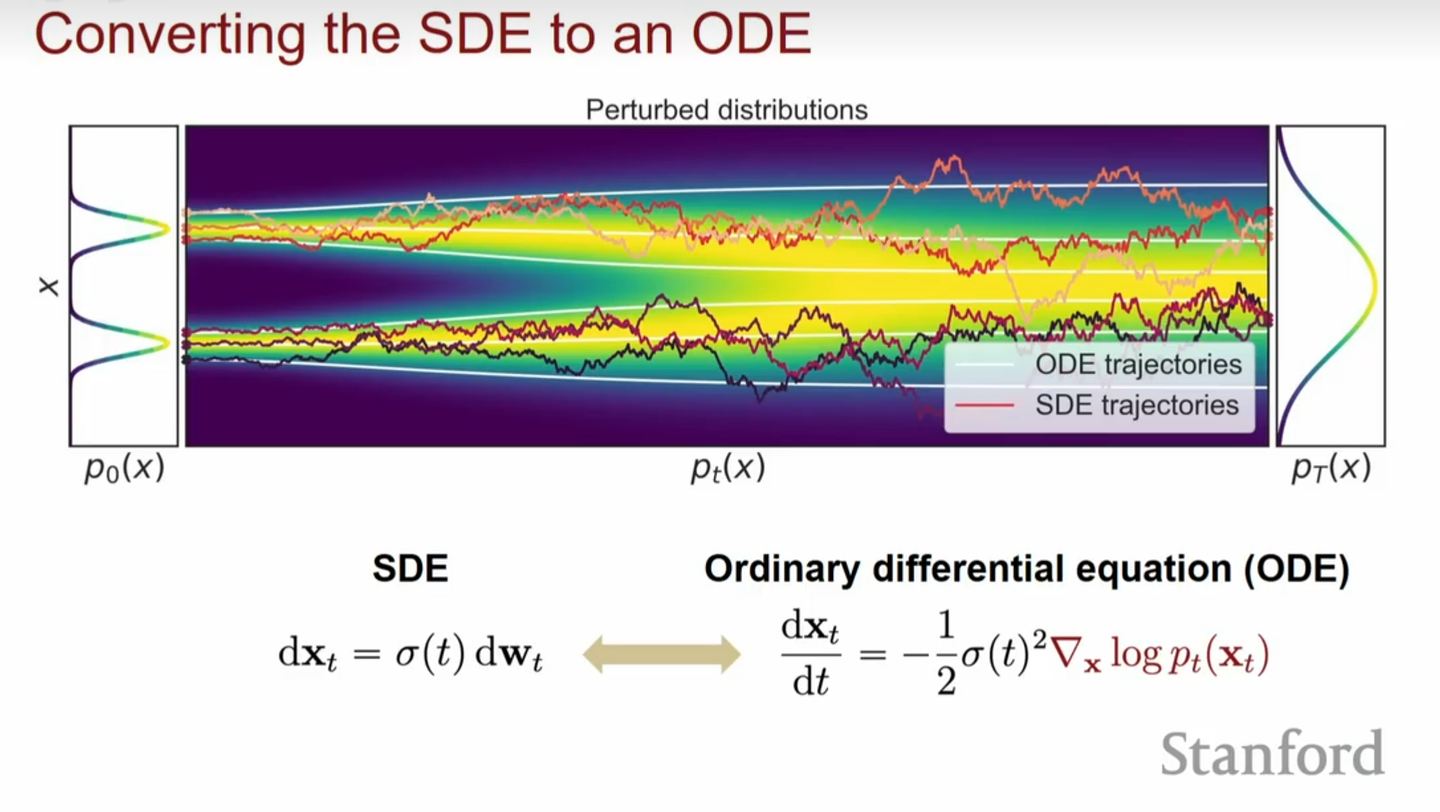
ODE形式有它的优点在于：

• 因为ODE比SDE好解，所以ODE的采样速度更快。
• 因为ODE是不带随机噪声的，整个过程是确定的，是可逆的，所以这个ODE也可以看做Normalizing flows，可以用来估计概率密度和似然。

但同时由于没有了随机噪声，可能导致多样性更差，实践中生成效果也不如SDE。