Diffusion Model原理

本学习笔记用于记录我学习Stanford CS236课程的学习笔记，分享记录，也便于自己实时查看。

引入

前面的课程中我们已经学习了许多生成模型的架构，例如VAEs，Score Based Models等。在课程的最后也是总算来到当前最火的生成模型架构：Diffusion Model。其实Diffusion Model与前面模型或多或少都有一定的联系，我们也可以从不同的视角来理解它。

笔者本科科研也算是学习研究了一些Diffusion相关的工作，但之前一直没有去梳理生成模型的发展，也没有深究其背后的数学原理。所以借此几乎，正好对一些知识进行整理，并对生成模型进行部分回顾。首先从DDPM和DDIM入手吧，这两篇文章也是之前科研实践学习过很多次了。

DDPM

首先我们知道，DDPM 是个马尔科夫模型（如下图），DDPM包括两个步骤。这两个步骤在原文中定义为前向加噪（forward，下图从右到左）和后向去噪（reverse，下图从左到右）。

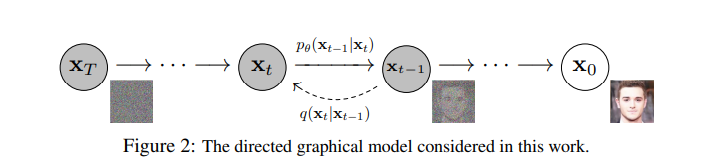
从\(x_0\)到\(x_T\)的过程就是前向加噪过程，我们可以看到加噪过程就是对原始图片\(x_0\)不断添加噪声，使其最后信噪比趋近于0，此时得到的图片也就变成噪声了，而与之相对应的去噪过程就是还原过程，即从噪声不断去噪还原为图片。

我们通过往图片中加入噪声，使得图片变得模糊起来，当加的步骤足够多的时候（也就是T的取值越大的时候，一般取1000），图片已经非常接近一张纯噪声。纯噪声也就意味着多样性，我们的模型在去噪（还原）的过程中能够产生更加多样的图片。

这里的操作实际上就是指在图片加入噪声\(noise\)，噪声\(noise\)本身的分布可以是很多样的（btw，保研还被问过这个问题），而论文中采用的是标准正态分布，其理由是考虑到其优良的性质，在接下来的公式推理中见到。

推导

从上面的图可知，DDPM 将前向过程和逆向过程都设计为了马尔可夫链的形式：

• 称从\(x_0\)到\(x_T\)的马尔可夫链为前向过程 (forward process) 或扩散过程 (diffusion process)；
• 称从\(x_T\)到\(x_0\)的马尔可夫链为逆向过程 (reverse process) 或去噪过程 (denoising process).

所以我们的损失函数通过极大似然估计来进行。但这里我们又会遇到和VAE一样的问题，\(log(P(x))\)中的\(P(x)\)需要对\(x_{1:T}\)进行积分，此时我们便可以效仿VAE的做法，即把\(x_{1:T}\)作为类似VAE中的潜变量，去优化对数似然的下界ELBO（为什么是下界可以参考我都VAEs的文章，简单来说就是用琴生不等式即可）：

\[ \begin{align*} ELBO &= \mathbb{E}_{\mathbf{x}_{1:T} \sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \left[\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \right] \\&= \mathbb{E}_{\mathbf{x}_{1:T} \sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \left[ \log \frac{p(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)}{\prod_{t=1}^T q(\mathbf{x}_t \vert \mathbf{x}_{t-1})} \right] \end{align*} \]

至于这里为啥要在给定\(x_0\)下计算，一方面是单纯的\(q(\mathbf{x}_{1:T})\)我们没办法计算得出，而\(q(\mathbf{x}_{1:T}|\mathbf{x}_0)\)我们能求出其闭式解，另一方面在训练时我们的确已经\(x_0\)的信息。

OK，我们继续进行推导

\[ \begin{align} &\ \ \ \ \ \text{ELBO}(\mathbf x_0) \\ &=\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)\prod_{t=1}^{T}p(\mathbf x_{t-1}\vert\mathbf x_t)}{\prod_{t=1}^{T}q(\mathbf x_t\vert\mathbf x_{t-1})}\right]\\ &=\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)\prod_{t=1}^{T}p(\mathbf x_{t-1}\vert\mathbf x_t)}{q(\mathbf x_1\vert\mathbf x_0)\prod_{t=2}^{T}q(\mathbf x_t\vert\mathbf x_{t-1},\mathbf x_0)}\right]\\ &=\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)\prod_{t=1}^{T}p(\mathbf x_{t-1}\vert\mathbf x_t)}{q(\mathbf x_1\vert\mathbf x_0)\prod_{t=2}^{T}\frac{q(\mathbf x_t\vert\mathbf x_0)q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)}{q(\mathbf x_{t-1}\vert\mathbf x_0)} }\right]\\ &=\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)\prod_{t=1}^{T}p(\mathbf x_{t-1}\vert\mathbf x_t)}{q(\mathbf x_T\vert\mathbf x_0)\prod_{t=2}^{T}q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)}\right]\\ &=\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log p(\mathbf x_0\vert\mathbf x_1)\right]+\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)}{q(\mathbf x_T\vert\mathbf x_0)}\right]+\sum_{t=2}^T\mathbb E_{q(\mathbf x_{1:T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_{t-1}\vert\mathbf x_t)}{q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)}\right]\\ &=\mathbb E_{q(\mathbf x_{1}\vert\mathbf x_0)}\left[\log p(\mathbf x_0\vert\mathbf x_1)\right]+\mathbb E_{q(\mathbf x_{T}\vert\mathbf x_0)}\left[\log\frac{p(\mathbf x_T)}{q(\mathbf x_T\vert\mathbf x_0)}\right]+\sum_{t=2}^T\mathbb E_{q(\mathbf x_t\vert\mathbf x_0)}\mathbb E_{q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)}\left[\log\frac{p(\mathbf x_{t-1}\vert\mathbf x_t)}{q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)}\right]\\ &=\underbrace{\mathbb E_{q(\mathbf x_{1}\vert\mathbf x_0)}\left[\log p(\mathbf x_0\vert\mathbf x_1)\right]}_\text{reconstruction term}-\underbrace{\text{KL}(q(\mathbf x_T\vert\mathbf x_0)\Vert p(\mathbf x_T))}_\text{regularization term}-\sum_{t=2}^T\mathbb E_{q(\mathbf x_t\vert\mathbf x_0)}\underbrace{\left[\text{KL}(q(\mathbf x_{t-1}\vert\mathbf x_t,\mathbf x_0)\Vert p(\mathbf x_{t-1}\vert\mathbf x_t))\right]}_\text{denoising matching terms} \end{align} \]

同样出现了重构项、正则项和匹配项。重构项要求\(x_1\)能够重构\(x_0\)，正则项要求\(x_T\)的后验分布逼近先验分布，而匹配项则建立起相邻两项\(x_{t−1},x_t\)之间的联系。

现在，我们只需要为式中出现的所有概率分布设计具体的形式，就可以代入计算了。为了让 KL 散度可解，一个自然的想法就是把它们都设计为正态分布的形式。

前向过程

在DDPM的前向过程中，对于\(t \in [1,T]\)时刻，\(x_t\)和\(x_{t-1}\)满足如下关系：

\[x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t }\epsilon, \ \ \ \epsilon\sim N(0,1)\]

其中\(β_t∈(0,1)\)是事先指定的超参数，代表从\(x_{t−1}\)到\(x_t\)这一步的方差。

这里的系数设定为开根号的\(\beta\)，是为了保证马尔科夫链的最后收敛为标准高斯分布。

\(\sqrt\beta\)和\(\sqrt{1-\beta}\)是怎么来的：

我们这里先不管\(\beta\)，把两个系数分别设为\(a\)和\(b\)。

公式变为：

\[x_t = ax_{t-1} + b\epsilon\]

我们希望，当\(t\)趋于无穷的时候，\(x_t \sim N(0,1), x_{t-1} \sim N(0,1)\)

我们知道当两个高斯分布相加时，

\[X\sim N(\mu_X,\sigma_X^2),Y\sim N(\mu_Y,\sigma_Y^2)\]

\[Z=aX+bY\]

则

\[Z \sim N(a\mu_X+b\mu_Y, a^2\sigma^2+b^2\sigma^2)\]

所以此时

\[x_t~\sim N(a\mu_{t-1}+b\mu_\epsilon,a^2\sigma_{t-1}^2+b^2\sigma_\epsilon^2)\]

\[x_t\sim N(a·0+b·0, a^2·1+b^2·1)\]

\[x_t \sim N(0,a^2+b^2)\]

我们想让\(x_{t-1}\)和\(\epsilon\)得到的\(x_{t}\)也服从标准正态分布，即\(x_{t} \sim N(0,1)\)，那么我们就只能让\(a^2+b^2=1\)。

再令\(\beta=a^2\)，则\(a=\sqrt{\beta},b=\sqrt{1-\beta}\)。

或者也可以令\(\alpha=b^2\)，则\(a=\sqrt{\alpha}x_{t-1}+\sqrt{1-\alpha}\epsilon\)。

说白了，这俩系数就是为了让两个服从标准正态分布的噪声相加得到的东西还是服从正态分布。

OK，在这基础上我们可以继续推导，让\(x_t\)用\(x_0\)来表示：

令\(\alpha_t=1-\beta_t\)，则公式变为：

\[x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\epsilon\]

继续推导：

\[\begin{align*} x_t &=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\epsilon\\ &=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1} }x_{t-2}+\sqrt{1-\alpha_{t-1} }\epsilon)+\sqrt{1-\alpha_t}\epsilon\\ &=\sqrt{\alpha_t\alpha_{t-1} }x_{t-2}+\sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon + \sqrt{1-\alpha_t}\epsilon\\ \end{align*}\]

上式最后一行第二项和第三项，可以看做两个正态分布相加。

由于两个正态分布\(X\sim N(\mu_x,\sigma_x^2), Y\sim N(\mu_y, \sigma_y^2)\)，相加后有

\(aX+bY\sim N(a\mu_x+b\mu_y,a^2\sigma_x^2+b^2\sigma_y^2)\)。所以，合并两个正态分布，得到：

\[x_t=\sqrt{\alpha_t\alpha_{t-1} }x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1} }\epsilon\]

由数学归纳法，可以推导出：

\[x_t=\sqrt{\alpha_t\alpha_{t-1}...\alpha_1}x_0+\sqrt{1-\alpha_t\alpha_{t-1}...\alpha_1}\epsilon\]

再令\(\bar\alpha_t=\alpha_t\alpha_{t-1}...\alpha_1\)，则公式可以进一步化简为：

\(x_t=\sqrt {\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_{t} }\epsilon\)，由于

\[\lim_{t\to\infty}\sqrt{\bar\alpha_t}=0,\quad\lim_{t\to\infty}\sqrt{1-\bar\alpha_t}=1\]

所以我们能够保证马尔科夫链最后能够收敛于标准正态分布

逆向过程

这里从我们熟知的贝叶斯公式出发：

\[P(A|B)=\frac{P(B|A)P(A)}{P(B)}\]

可知

\[P(x_{t-1}|x_t)=\frac{P(x_t|x_{t-1})P(x_{t-1})}{P(x_t)}\]

这里我们的\(P(x_{t-1})\)和\(P(x_t)\)我们都不知道，但在已知\(x_0\)的情况下有：

\[P(x_{t-1}|x_t,x_0)=\frac{P(x_t|x_{t-1},x_0)P(x_{t-1}|x_0)}{P(x_t|x_0)}\]

把\(x_0=\sqrt{\bar{\alpha_t} }x_0\)和\(x_t=\sqrt {\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_{t} }\epsilon\)带入上式，可得：

\[P(x_{t-1}|x_t,x_0)=\frac{ N(\sqrt{\alpha_t}x_0,1-\bar\alpha_t) N(\sqrt{\bar\alpha_{t-1} }x_0,1-\bar\alpha_{t-1}) }{ N(\sqrt{\bar\alpha_{t} }x_0,1-\bar\alpha_{t}) }\]

已知高斯分布的概率密度函数为：

\[f(x)=\frac{1}{\sqrt{2\pi\sigma} }exp(-\frac{(x-\mu)^2}{2\sigma^2})\]

所以

\[P(x_{t-1}|x_t,x_0) \propto exp-\frac{1}{2} [ \frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{1-\alpha_t} +\frac{(x_{t-1}-\sqrt{\bar\alpha_{t-1} }x_0)^2}{1-\bar\alpha_{t-1} } -\frac{(x_{t}-\sqrt{\bar\alpha_{t} }x_0)^2}{1-\bar\alpha_{t} } ]\]

此时由于\(x_{t-1}\)是我们关注的变量，所以整理成关于\(x_{t-1}\)的形式：

\[P(x_{t-1}|x_t,x_0) \propto exp-\frac{1}{2} [ (\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar\alpha_{t-1} })x_{t-1}^2 -(\frac{-2\sqrt{\alpha_t}x_t}{1-\alpha_t} + \frac{-2\sqrt{\bar\alpha_{t-1} }x_0}{1-\bar\alpha_{t-1} })x_{t-1} +C(x_t,x_0) ]\]

其中第三项\(C(x_t,x_0)\)与\(x_{t-1}\)无关，作为指数上相加的部分，可以拿到最前面只影响最前面的系数。

所以此时：

\[P(x_{t-1}|x_t,x_0) \propto exp-\frac{1}{2} [ (\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar\alpha_{t-1} })x_{t-1}^2 -(\frac{-2\sqrt{\alpha_t}x_t}{1-\alpha_t} + \frac{-2\sqrt{\bar\alpha_{t-1} }x_0}{1-\bar\alpha_{t-1} })x_{t-1}]\]

又因为标准正态分布满足\(\propto exp - \frac{x^2-2\mu x + \mu^2}{2\sigma^2}\)，所以我们可以得到\(P(x_{t-1}|x_t,x_0)\)对应的方差

\[\frac{1}{\sigma^2}=\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar\alpha_{t-1} } =\frac{1-\alpha_t\bar\alpha_{t-1} }{(1-\alpha_t)(1-\bar\alpha_{t-1})} =\frac{1-\bar\alpha_{t} }{(1-\alpha_t)(1-\bar\alpha_{t-1})}\]

这里\(\alpha_t\bar\alpha_{t-1}=\bar\alpha_t\)。所以：

\[\sigma^2=\frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\]

再看\(x_{t-1}\)的一次项，得到：

\[\frac{2\mu}{\sigma^2}= (\frac{-2\sqrt{\alpha_t}x_t}{1-\alpha_t} + \frac{-2\sqrt{\bar\alpha_{t-1} }x_0}{1-\bar\alpha_{t-1} })\]

把\(\sigma^2\)和\(x_0\)带入上式，化简得到： \[\mu=\frac{1}{\sqrt{\alpha_t} }(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t} }\epsilon)\]

所以说： \[P(x_{t-1}|x_t, x_0)\sim N(\frac{1}{\sqrt{\alpha_t} }(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t} }\epsilon), \frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t})\]

回顾一下我们写的这一大段公式，也就是说，我们已知了先验概率，推导出了后验概率的表达式，得到了在给定\(x_0\)后的\(x_{t-1}\)的分布的均值和方差。也就是说，上面公式中，我们的

\[q(x_{t-1}\vert x_t,x_0)\sim N(\frac{1}{\sqrt{\alpha_t} }(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t} }\epsilon), \frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t})\]

接下来，\(\epsilon\)的具体值，我们让模型去拟合就好了。

损失函数

我们之前已经推导了ELBO的具体形式：

\[\text{ELBO}= \underbrace{E_{x_1\sim q(x_1\vert x_0)}[\log p_\theta(x_0\vert x_1)]}_{ {L_0} }- \underbrace{KL(q(x_T \vert x_0)\|p(x_T))}_{ {L_T} }- \sum_{t=2}^T\underbrace{E_{x_t\sim q(x_t\vert x_0)}\left[KL(q(x_{t-1}\vert x_t,x_0)\|p_\theta(x_{t-1}\vert x_t))\right]}_{ {L_{t-1} }}\]

这里\(q(x_{t-1}\vert x_t,x_0)\)我们已经得到了，\(q(x_{t}|x_0)\)也是我们定义的。只需要定义\(p_\theta(x_{t-1}|x_t)\)即可，为了计算方便，我们也选择与\(q(x_{t-1}\vert x_t,x_0)\)一样的形式。

\[p_\theta(\textbf{x}_{t-1}|\textbf{x}_t) = \mathcal{N}(\textbf{x}_{t-1}; \mu_\theta(\textbf{x}_t, t), \frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}I)\]

其中\(\boldsymbol{\mu}_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t} } \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} } \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)\)，而\({\epsilon}_\theta(\mathbf{x}_t, t)\)就是我们模型的输出。此时，我们带入可以得到

\[\begin{align} \mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t} } ( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} } {\epsilon}_\theta(\mathbf{x}_t, t) ), \frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}I) \end{align}\]

带入上面KL散度的公式，可以得到损失函数\(L_t\)便为：

\[\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon} } \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu} }_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon} } \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t} } \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} } \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t} } \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t} } \boldsymbol{\boldsymbol{\epsilon} }_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon} } \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon} } \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}\]

发现可以使用不用权重的简单形式就可以训练得到好的结果，即

\[\begin{aligned} L_\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}\]

这样，我们就获得了DDPM的最终目标函数：

\[L_\text{simple}(\theta)=\mathbb E_{t,x_0,\epsilon}\left[\Vert\epsilon-\epsilon_\theta(x_t,t)\Vert^2\right]\]

具体训练流程和采样流程如下：

DDIM

DDPM虽好，但它只能一步一步老老实实通过\(x_{t}\)预测\(x_{t-1}\)，不能跨步运算，如果\(T =1000\)，那么生成一整图像就需要用网络推理1000次，效率很低。于是为了结局这个问题，DDIM出现了，而且最巧妙的是它不需要重新训练模型。

DDIM始于一个假设，它假设了

\[P(x_{prev}|x_t,x_0)\sim N(kx_0+mx_t,\sigma_2)\]

\[x_{prev}=kx_0+mx_t+\sigma\epsilon,\ \ \ \ \ \epsilon\sim N(0,1)\]

又因为加噪过程满足公式\(x_t=\sqrt {\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_{t} }\epsilon\)

把\(x_t\)带入\(x_{t-1}\)合并同类项得到：

\[\begin{align*} x_{prev}&=kx_0+m(\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon)+\sigma\epsilon\\ &=(k+m\sqrt{\bar\alpha_t})x_0+\epsilon' \end{align*}\]

\[\epsilon'\sim N(0,m^2(1-\bar\alpha_t)+\sigma^2)\]

又因为\(x_{prev}=\sqrt {\bar\alpha_{prev} }x_0+\sqrt{1-\bar\alpha_{prev} }\epsilon\)，满足对应系数相同，有：

\[k+m\sqrt{\bar\alpha_t}=\sqrt{\bar{\alpha_{prev} }}\\ m^2(1-\bar\alpha_t)+\sigma^2=1-\bar\alpha_{prev}\]

求得：

\[m=\frac{\sqrt{1-\bar\alpha_{prev}-\sigma^2} }{\sqrt{1-\bar\alpha_t} }\\ k=\sqrt{\bar\alpha_{prev} }-\frac{\sqrt{1-\bar\alpha_{prev}-\sigma^2} }{\sqrt{1-\bar\alpha_t} }\sqrt{\bar\alpha_t}\]

带入公式最终化简得：

\[x_{prev}=\sqrt{\bar{\alpha_{prev} }} (\frac{x_t-\sqrt{1-\bar\alpha_t}\epsilon_t}{\sqrt{\bar\alpha_t} }) +\sqrt{1-\bar\alpha_{prev}-\sigma^2}\epsilon_t+\sigma^2\epsilon\]

其中\(t\)和\(prev\)可以相隔多个迭代步数，一般相隔20可以做到采样速度和采样质量比较好地平衡。所以一般DDPM要做1000步，而DDIM是需要50步就可以完成采样。

当这里的\(\sigma\)选取0的时候，也就意味着变成了一个确定性采样的过程。此时的DDIM就变成了一个Flow Models，事实上论文里也是这么做的。

从不同角度看扩散模型

前面我们DDPM的推导过程中，其实可以把扩散模型看成一个给定后验的多层VAE。即认为设定了\(p(x_{1:T}|x_0)\)的形式，然后让模型来从潜变量中采样，最终生成图片。

而DDIM把这个过程变成了一个确定性过程，也就是说把潜变量和数据之间做了一个双射，所以此时也就可以看成Flow Models的一个了

事实上，扩散模型的连续和离散其实对应着随机过程里的概念。一般来说，discrete time指的是随机过程中的时间\(t\)只能取离散整数值，而continous-time则指的是时间参数\(t\)可以取连续值。discrete time随机过程中的参数在一个离散的时间点只能改变一次；而continuous-time随机过程的参数则可以随时发生变化。

DDPM和SDE

我们在DDPM里的加噪过程。每一个time step，我们都会按照如下的离散马尔可夫链进行加噪：

\[x_i = \sqrt{1 - \beta_i}x_{i-1} + \sqrt{\beta_i} \epsilon_{i-1}, i=1,..., N\]

为了将上述过程连续化，我们需要引入连续时间随机过程。而连续时间其实就是让每个离散的时间间隔\(\Delta t\)无限趋近于0，其实也等价于求出\(N \to \infty\)​时，上述马尔可夫链的极限

在求极限之前，我们需要先引入一组辅助的noise scale\(\{\bar{\beta}_i = N \beta_i\}_{i=1}^N\)，并将上面的式子改写如下：

\[x_i = \sqrt{1 - \frac{\bar{\beta}_i}{N} }x_{i-1} + \sqrt{\frac{\bar{\beta}_i}{N} }\epsilon_{i-1}, i = 1,..., N\]

在\(N \to \infty\)​时，上面的\(\{\bar{\beta}_i\}_{i=1}^{N}\)就成了一个关于时间\(t\)的连续函数\(\beta(t)\)​，并且\(t \in [0, 1]\)。随后，我们可以假设\(\Delta t = \frac{1}{N}\)​，在每个\(i\Delta t\)时刻，连续函数\(\beta(t), x(t), \epsilon(t)\)都等于之前的离散值，即：

\[\beta(\frac{i}{N}) = \bar{\beta}_i, x(\frac{i}{N}) = x_i, \epsilon(\frac{i}{N})=\epsilon_i\]

在\(t \in \{0, 1, ..., \frac{N-1}{N}\}\)​以及\(\Delta t=\frac{1}{N}\)的情况下，我们就可以用连续函数改写之前的式子：

\[\begin{align} x(t+ \Delta t) &= \sqrt{1-\beta(t+\Delta t)\Delta t}\ x(t) + \sqrt{\beta(t+\Delta t)\Delta t}\ \epsilon(t) \\ & \approx x(t) - \frac{1}{2}\beta(t+\Delta t) \Delta t\ x(t) + \sqrt{\beta(t+\Delta t)\Delta t}\ \epsilon(t) \\ & \approx x(t) - \frac{1}{2}\beta(t)\Delta t\ x(t) + \sqrt{\beta(t)\Delta t}\ \epsilon(t) \end{align}\]

上面的近似只有在\(\Delta t \ll 1\)时成立。我们将其再移项后就可以得到下式：

\[x(t+\Delta t) - x(t) \approx -\frac{1}{2} \beta(t)\Delta t\ x(t) + \sqrt{\beta(t)\Delta t}\ \epsilon(t) \\ \mathrm{d} x = -\frac{1}{2}\beta(t)x \mathrm{d}t + \sqrt{\beta(t)} \mathrm{d}w\]

其中，\(w\)​表示的就是Wiener Process。这里面的第二个式子，就是一SDE方程。

至此，我们证明了DDPM连续化之后，就可以得到一个SDE方程，并且它是一种Variance Preserving的SDE。Variance Preserving的含义是当\(t \to \infty\)时，它的方差依然有界。

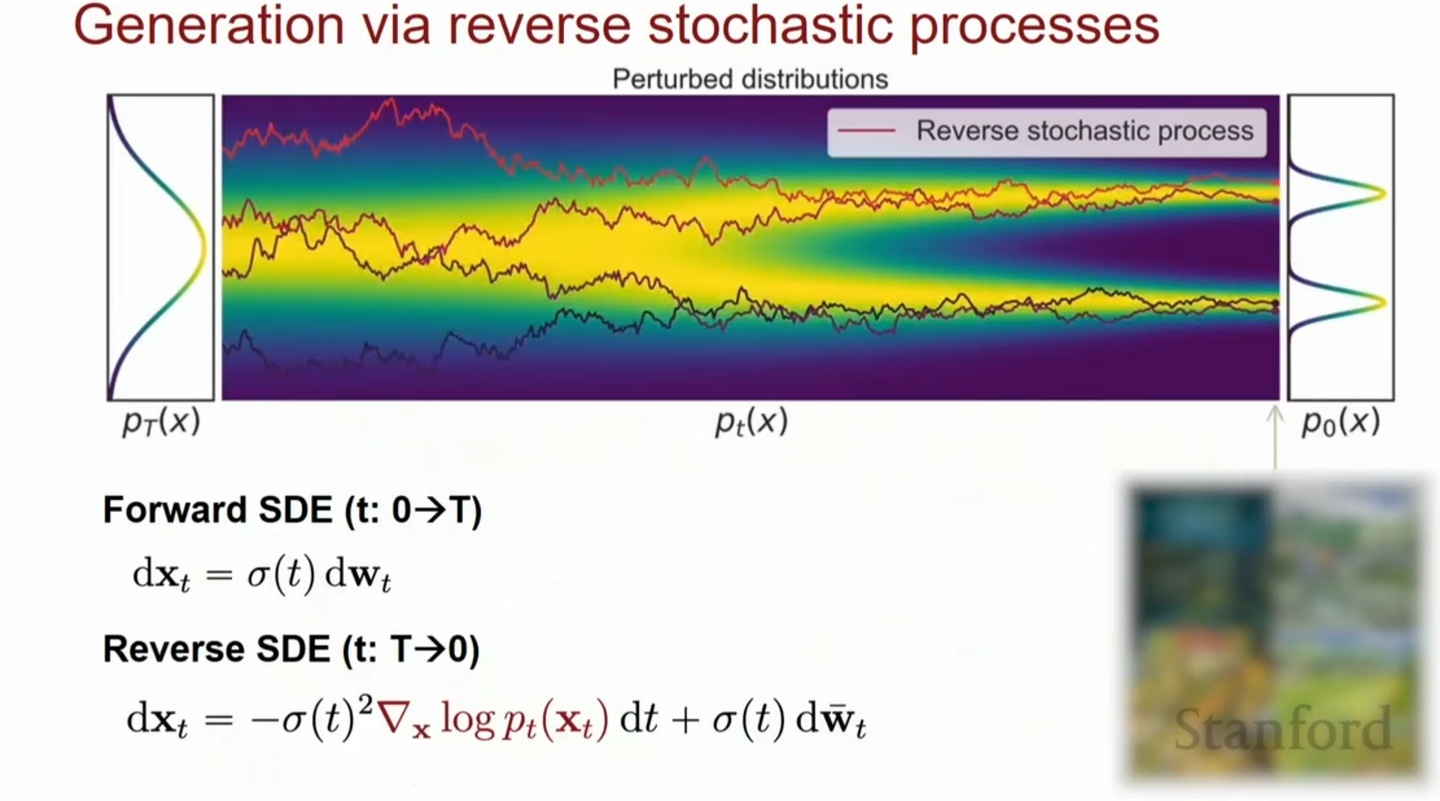
与此反向过程也是一个SDE方程，称为reverse SDE：

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - g^2(t)\nabla _{\mathbf{x} }\log p(\mathbf{x})]\text{d}\mathbf{t} + g(t)\text{d}\mathbf{w}\]

这个反向过程中的未知量就只有分数函数\(\nabla_x \log p_{t}(x)\)​。至此，DDPM和分数模型也产生了联系，实际上二者之间是相互等价的。而DDPM和分数模型本质上都是在学习这个reverse SDE的解。 我们可以看到，DDPM每一步的去噪其实本质上与Annealed Langevin dynamics是一模一样的。

DDIM与ODE

首先对于一个SDE，

\[\text{d}\mathbf{x}= \mathbf{f}(\mathbf{x}, t)\text{d}\mathbf{t} + g(t)\text{d}\mathbf{w}\]

我们写出它的福克-普朗克方程（Fokker-Planck equation）：

\[\begin{align*} \nabla _{t}p(\mathbf{x}, t) &= -\nabla _{\mathbf{x} }[\mathbf{f}(\mathbf{x}, t)p(\mathbf{x}, t)] + \frac{1}{2}g^{2}(t)\nabla _{\mathbf{x} }^{2}p(\mathbf{x}, t)\\ &= -\nabla _{\mathbf{x} }[\mathbf{f}(\mathbf{x}, t)p(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}p(\mathbf{x}, t)] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x} }^{2}p(\mathbf{x}, t)\\ &= -\nabla _{\mathbf{x} }[(\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}\log p(\mathbf{x}, t))p(\mathbf{x})] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x} }^{2}p(\mathbf{x}, t)\\\end{align*}\]

现在我们把福克-普朗克方程变成了这样：

\[\nabla_{t}p(\mathbf{x}, t) = -\nabla_{\mathbf{x} }[(\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_\mathbf{x}\log p(\mathbf{x}, t))p(\mathbf{x})] + \frac{1}{2}\sigma^{2}(t)\nabla _{\mathbf{x} }^{2}p(\mathbf{x}, t)\]

其对应的SDE为：

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}(g^{2}(t) - \sigma^{2}(t))\nabla_{\mathbf{x} }\log p_{t}(\mathbf{x})]\text{d}\mathbf{t} + \sigma(t)\text{d}\mathbf{w}\]

因为前后两个SDE是等价的，他们对应的\(p_{t}(\mathbf{x})\)是一样的，意味着我们可以改变第二个SDE的方差\(\sigma(t)\)。当我们取\(\sigma(t)=0\)，可以得到一个常微分方程(Ordinary Differential Equation, ODE),

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g^{2}(t)\nabla_ {\mathbf{x} }\log p_{t}(\mathbf{x})]\text{d}\mathbf{t}\]

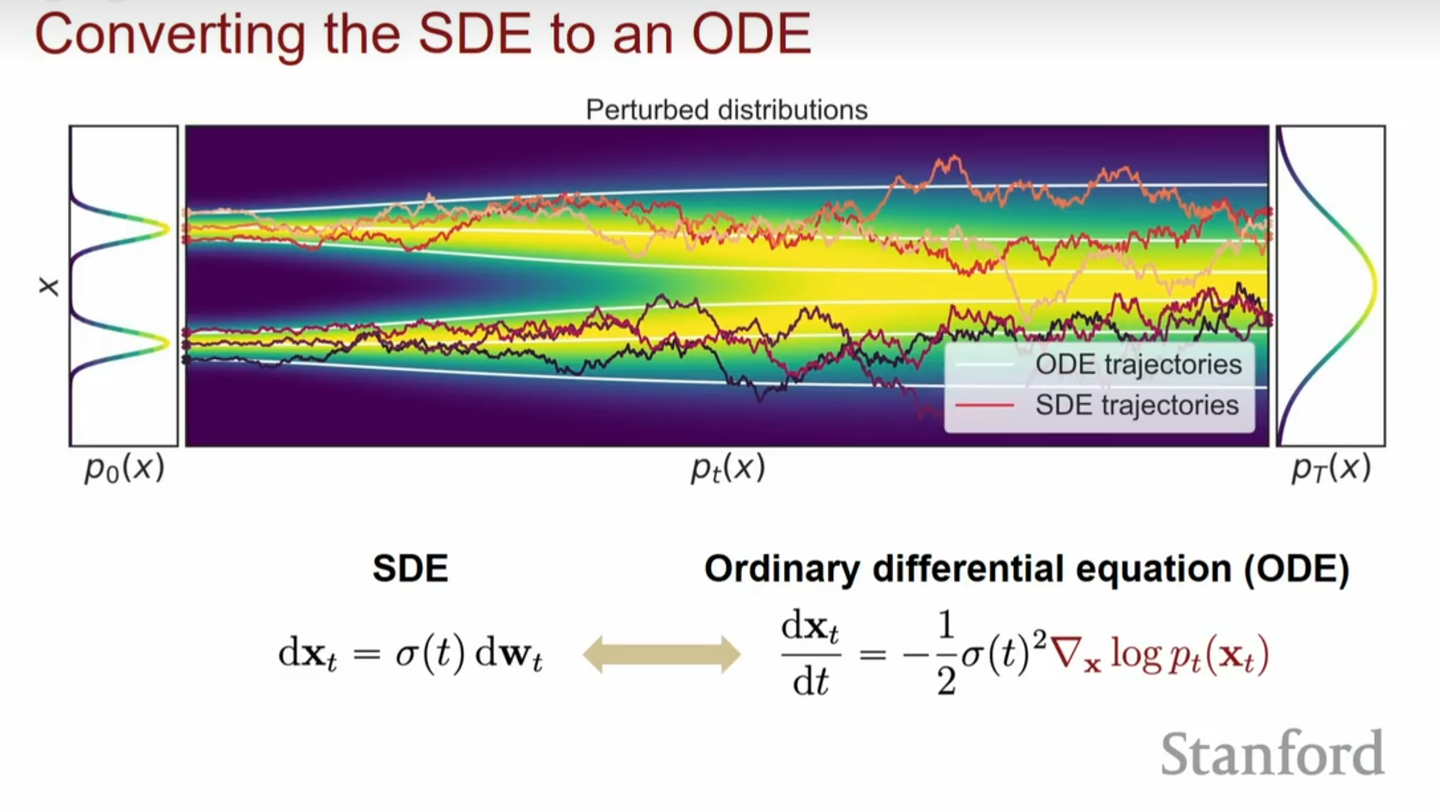
这个结论有什么作用呢？首先，我们其实更在乎的是边缘概率分布\(q_t(x)\)，因为我们需要保证它在足够长的时刻\(T\)，\(q_T(x)\)可以变成一个纯噪声，同时我们还需要\(q_0(x)\)​符合原始数据分布。上述结论可以保证这一点。同时，扩散模型本质上是在学习一个扩散过程的逆过程，既然前向SDE存在一个对应的ODE，那么反向过程reverse SDE其实也有一个对应的ODE，这个反向过程对应的ODE形式也是上面的式子。

而 DDIM 恰是一种确定性情形，所以我们自然会想到——能不能用 ODE 来描述一个 DDIM 呢？答案是肯定的。DDIM的公式如下：

\[\begin{align} x_{t-1}&=\sqrt{\bar\alpha_{t-1} }x_\theta(x_t,t)+\sqrt{1-\bar\alpha_{t-1} }\epsilon_\theta(x_t,t)\\ &=\frac{\sqrt{\bar\alpha_{t-1} }}{\sqrt{\bar\alpha_t} }\left(x_t-\sqrt{1-\bar\alpha_t}\epsilon_\theta(x_t,t)\right)+\sqrt{1-\bar\alpha_{t-1} }\epsilon_\theta(x_t,t) \end{align}\]

两边均减去\(x_t\)，得：

\[\begin{align} x_{t-1}-x_t&=\frac{1}{\sqrt{\bar\alpha_t} }\left[\left(\sqrt{\bar\alpha_{t-1} }-\sqrt{\bar\alpha_t}\right)x_t-\left(\sqrt{\bar\alpha_{t-1}(1-\bar\alpha_t)}-\sqrt{\bar\alpha_t(1-\bar\alpha_{t-1})}\right)\epsilon_\theta(\mathbf x_t,t)\right]\\ &=\frac{1}{\sqrt{\bar\alpha_t} }\left(\frac{\bar\alpha_{t-1}-\bar\alpha_t}{\sqrt{\bar\alpha_{t-1} }+\sqrt{\bar\alpha_t} }x_t-\frac{\bar\alpha_{t-1}-\bar\alpha_t}{\sqrt{\bar\alpha_{t-1}(1-\bar\alpha_t)}+\sqrt{\bar\alpha_t(1-\bar\alpha_{t-1})} }\epsilon_\theta(x_t,t)\right)\\ &=\frac{\bar\alpha_{t-1}-\bar\alpha_t}{\sqrt{\bar\alpha_t} }\left(\frac{x_t}{\sqrt{\bar\alpha_{t-1} }+\sqrt{\bar\alpha_t} }-\frac{\epsilon_\theta(\mathbf x_t,t)}{\sqrt{\bar\alpha_{t-1}(1-\bar\alpha_t)}+\sqrt{\bar\alpha_t(1-\bar\alpha_{t-1})} }\right) \end{align}\]

记\(x(t)=x_t,\barα(t)=\barα_t\)，将\(t-1\)换成\(t−Δt\)并令\(Δt→0\)，得：

\[\mathrm dx=\frac{\mathrm d\bar\alpha(t)}{\sqrt{\bar\alpha(t)} }\left(\frac{x(t)}{2\sqrt{\bar\alpha(t)} }-\frac{\epsilon_\theta(x(t),t)}{2\sqrt{\bar\alpha(t)(1-\bar\alpha(t))} }\right)=\frac{\bar\alpha'(t)}{2\bar\alpha(t)}\left(x(t)-\frac{\epsilon_\theta(x(t),t)}{\sqrt{1-\bar\alpha(t)} }\right)\mathrm dt\]

这就是 DDIM 的 ODE 描述。

在 DDPM 的设置下，有\(f(x,t)=−\frac{1}{2}β(t)x,g(t)=\sqrt{β(t)}\)，代入

\[\text{d}\mathbf{x}= [\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g^{2}(t)\nabla_ {\mathbf{x} }\log p_{t}(\mathbf{x})]\text{d}\mathbf{t}\]

得：

\[\mathrm dx=\left[-\frac{1}{2}\beta(t)x-\frac{1}{2}\beta(t)\nabla_{\mathbf{x} }\log p_{t}(\mathbf{x})\right]\mathrm dt=-\frac{1}{2}\beta(t)\left[x+\nabla_{\mathbf{x} }\log p_{t}(\mathbf{x})\right]\mathrm dt\]

与我们上面的式子对应。

既然引入了ODE，那么我们的模型就可以去学习如何解这个ODE，同时也可以引入各种传统的ODE solver例如：Euler method, Runge–Kutta method等一些方法。这就是为什么我们可以看到像Stable Diffusion之类的模型会有那么多sampler的原因，本质上都是一些ODE solver和SDE solver。但是后面的研究者发现，传统的ODE solver在采样效果上比不过DDIM，这就非常奇怪了。DPM-Solver的作者在他们的论文中给出了原因：DDIM充分利用了diffusion ODE的半线性结构（semi-linear structure），并且它是一个semi-linear ODE的一阶Solver，而传统的ODE solver并没有利用好这个半线性结构，因此DDIM的准确度会更高一些，因此采样效果也更好。

这里还需要注意的点是，diffusion ODE这类模型相比diffusion SDE存在着诸多好处，比如：

• 没有随机性，ODE是一个确定性过程，可以以更快的速度收敛，因此可以达到更快的采样速度
• 由于是确定性过程，可以计算数据似然（likelihood）等。