[Probabilistic Machine Learning]: Fundamentals-Probability

本学习笔记用于记录我学习Probabilistic Machine Learning的学习笔记，分享记录，也便于自己实时查看。

一、Probability基础知识

1. Probability space

概率空间是一个三元组$(Ω，F，P)$，其中$Ω$是样本空间，是实验可能结果的集合；$F$是事件空间，它是$Ω$所有可能子集的集合；$P$是概率函数，它是从事件$E \subsetΩ$到$[0,1]$中的一个数(即$P: F→[0,1]$)的映射，它满足一定的一致性等要求，具体如下：

2. 其它

离散随机变量定义，连续随机变量定义，条件概率，贝叶斯公式…

具体略过

二、常见分布

1. Discrete distributions

1.1 Bernoulli and binomial distributions：

伯努利分布和二项分布，也很熟悉了

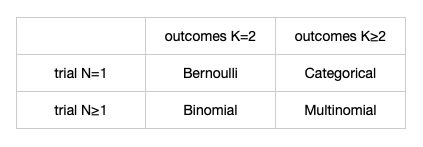
1.2 Categorical and multinomial distribution：

其实也就是对伯努利分布和二项分布在更多的类别上的分布：

1.3 Poisson distribution

泊松分布，本科课程也重点学习过**：**

1.4 Negative binomial distribution

负二项分布又称帕斯卡分布（巴斯卡分布），它表示，已知一个事件在伯努利试验中每次的成功的概率是$p$，在一连串伯努利实验中，直到失败$r$次，此时成功次数作为随机变量$x$。

$r=1$时，即为几何分布。

2. 分布在R上的Continuous distributions

2.1 Gaussian （Normal）

高斯分布，最经典的分布

2.2 Half-normal

半正态分布即一个高斯分布的绝对值（比如很多时候建模需要非负）

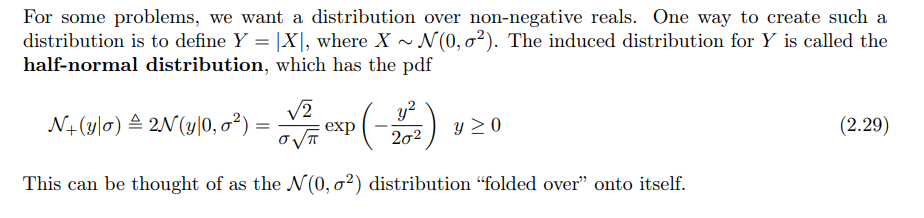
2.3 Student t-distribution

t-分布也比较熟悉了：

2.4 Cauchy distribution

Cauchy distribution是t-分布的特例：

2.5 Laplace distribution

拉帕拉斯分布也是很有名的分布，把高斯分布的平方改成了绝对值：

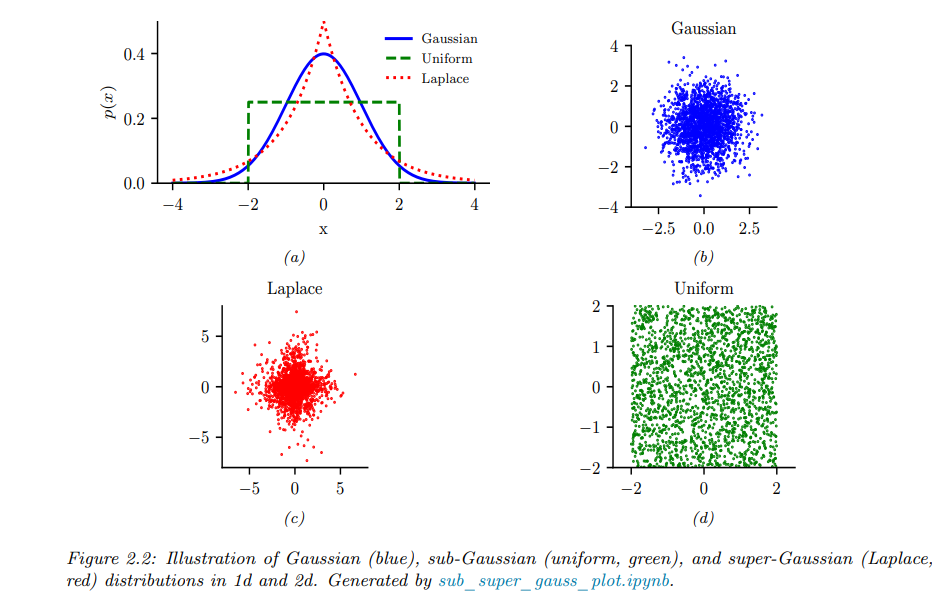
2.6 Sub-Gaussian and super-Gaussian distributions

其实就是比较尾部衰减速度。超高斯分布式指随机过程$X$的四阶累计量恒大于零，并且关于其均值对称分布。而亚高斯分布就是恒小于零。

例如拉普拉斯分布就是超高斯分布一种，而均匀分布就是亚高斯分布一种。

具体对比如图：

3. 分布在正实数上的Continuous distributions

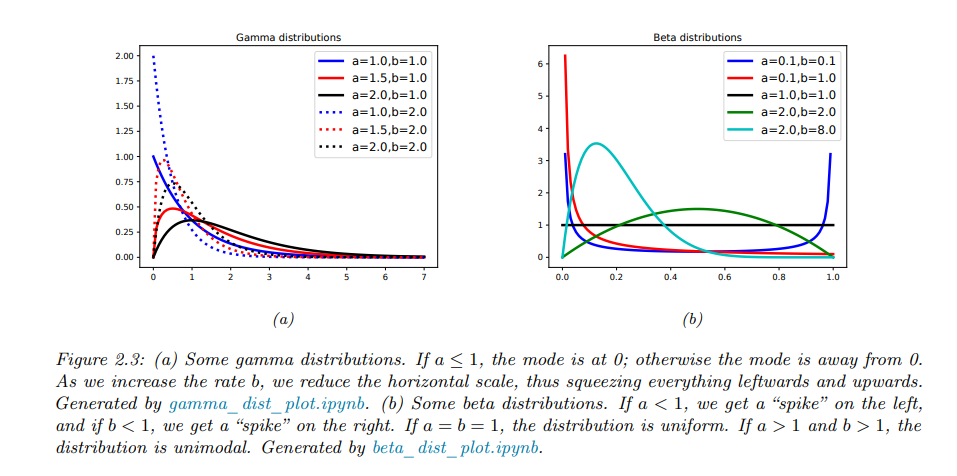
3.1 Gamma distribution

伽马分布以伽马函数为基础，非常灵活。

“指数分布”和“$χ^{2}$分布”都是伽马分布的特例。

概率分布的可视化如下：

3.2 Exponential distribution

指数分布，伽马分布的特例。本科课程也重点学习过。

3.3 Chi-squared distribution

$χ^{2}$分布，伽马分布的特例。也比较熟悉了。

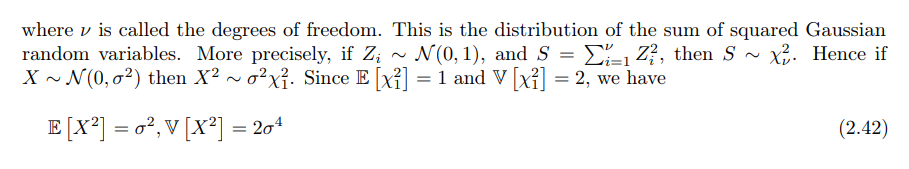
3.4 Inverse gamma

倒伽马分布是伽马分布变量的倒数。倒$χ^{2}$分布是其特例。

3.5 Pareto distribution

帕累托分布是以意大利经济学家维弗雷多·帕雷托命名的。 是从大量真实世界的现象中发现的幂定律分布。其形式如下：

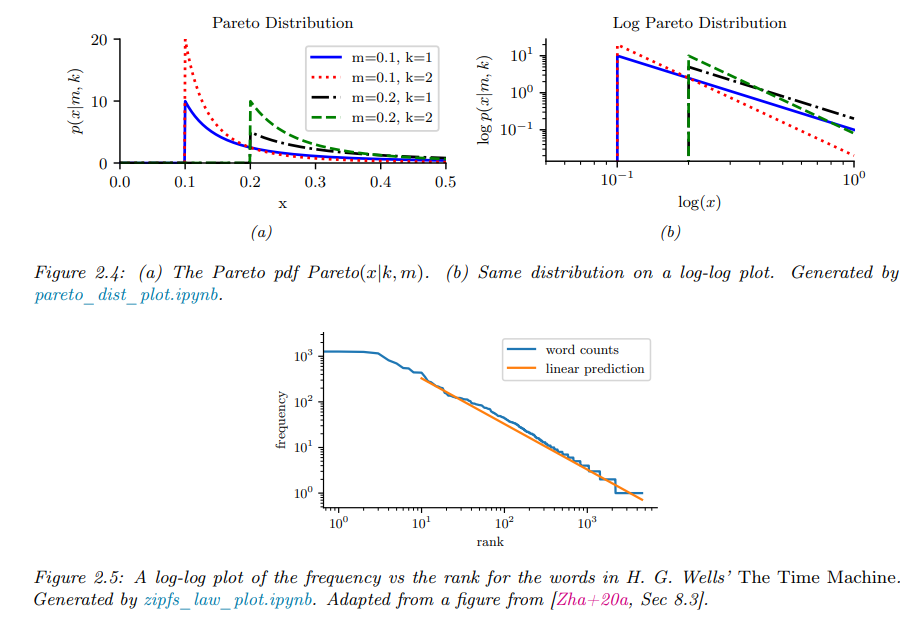
可以注意到，对概率分布取对数，则会得到一个线性函数，所以NLP中大名鼎鼎的齐夫定律便服从这个分布：

对于尾部比较大的分布的建模，帕累托分布是有用的，现实中许多形式的数据都具有这种特性。如：

• 财富在个人之间的分布（80%的人掌握20%的财富）
• 人类居住区的大小
• 对维基百科条目的访问

一般认为这是因为数据是由各种潜在因素产生的，当这些潜在因素混合在一起时，自然会导致这种重尾的分布。

其概率分布的直观展示如下：

4. 分布在[0, 1]上的Continuous distributions

4.1 Beta distribution

所谓的以$\alpha, \beta$为参数的 Beta 分布$f(x; \alpha, \beta)$，其实描述的就是我们在做抛硬币实验的过程中，我们当前如果已经观测到$\alpha + 1$次正面，$\beta + 1$次反面，那么此时硬币正面朝上的真实概率的可能性分布。

即，Beta 分布是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数。

5.Multivariate continuous distributions

5.1 Multivariate normal (Gaussian)

多元高斯函数是最重要最经典的多元分布了，下面会专门详细学习。

5.2 Multivariate Student distribution

多元t分布的形状与多元高斯比较类似，主要是峰值更低，尾部缩减更慢。

当$v$趋近于无穷时，其逐渐逼近多元高斯分布，其均值和协方差矩阵如下：

5.3 Circular normal (von Mises Fisher) distribution

现实中，有些数据仅仅分布于一个单位球上，而不是欧式空间的任何一点都有概率。此时，冯·米塞斯分布就是针对这种情况。

冯·米塞斯分布就是高斯分布在单位球上的拓展。

5.4 Matrix normal distribution (MN)

Matrix normal distribution是作用于矩阵的正态分布，其定义如下：

它可以转化为作用于向量上的多元高斯分布，只要将矩阵正态分布进行向量化处理便可以得到多元正态分布形式，如上所示。

这两者完全等价 (证明过程可以参考https://en.wikipedia.org/wiki/Matrix_normal_distribution)，公式中的符号$\otimes$表示 Kronecker积，$V\otimes U$表示多元正态分布的协方差矩阵；符号$\text{vec}\left(\cdot\right)$表示将给定矩阵按列组织成一个向量。

这两者完全等价，但在实践中，考虑到协方差矩阵$V\otimes U\in\mathbb{R}^{(mn)\times (mn)}$，假设我们想生成一个大小为$100\times 200$的随机矩阵$X$，并要求矩阵$X$在概率上服从矩阵正态分布。此时，若利用多元正态分布进行生成，则需要协方差矩阵$V\otimes U$的大小为$(100\times 200)\times (100\times 200)=20000\times 20000$，元素数量为$4\times 10^8$，显然，这个数字很惊人，毕竟存储这么大的矩阵就需要消耗计算机比较多的内存了，所以矩阵正态分布有它的优势。

5.5 Wishart distribution

Wishart分布是伽马分布的多元形式，也是十分重要的分布。卡方分布也是它的特例。

多元高斯分布和Wishart分布有很紧密的联系，设$Y_{1}\ldots Y_{n}\ iid\sim\ N(0,\Sigma)$，其中$Y_{i}(i = 1,\ldots,n)$是$p$维列向量，则随机矩阵$W = \sum_{i = 1}^{n}{Y_{i}Y_{i}^{T}}$的分布就是wishart分布，记作$W\sim Wishart(\Sigma,n)$，可以发现，当协方差矩阵退化为单位1，得到的就是卡方分布。

5.6 Inverse Wishart distribution

与倒伽马分布和伽马分布的关系类似，服从Wishart分布的随机变量的倒数就服从倒Wishart分布。

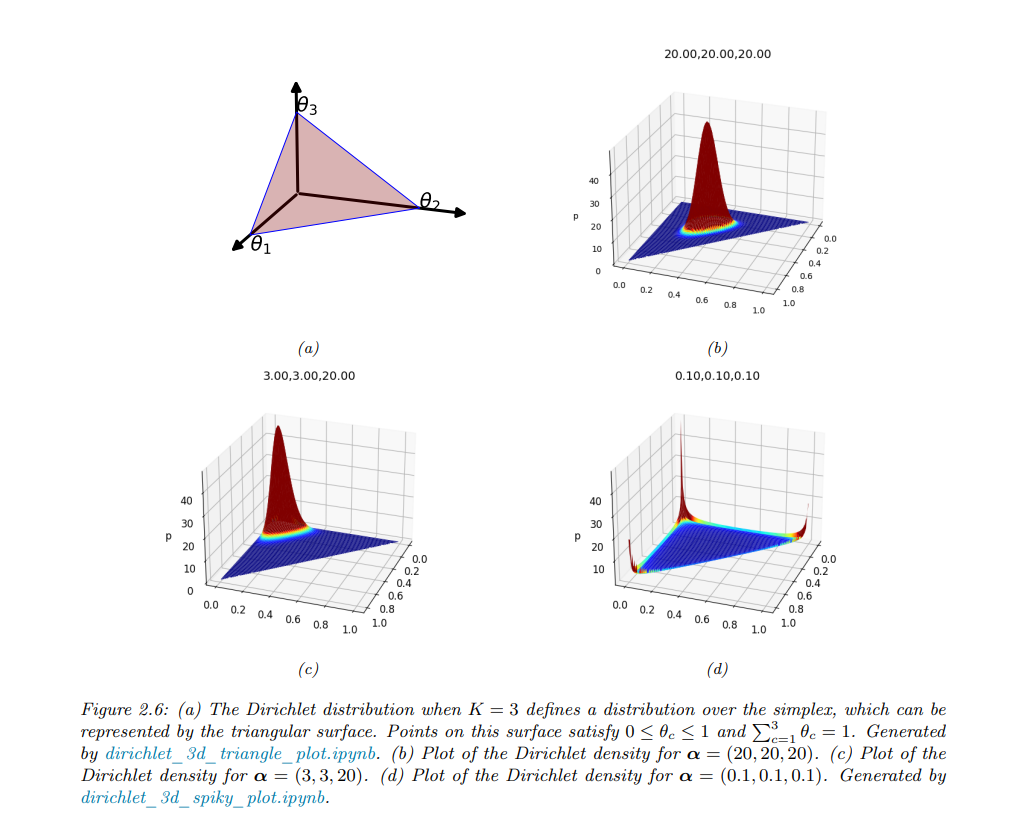
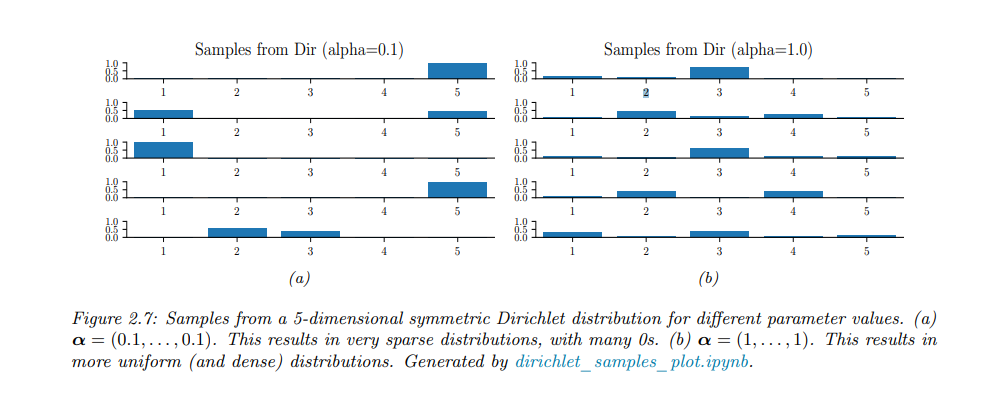
5.7 Dirichlet distribution

狄利克雷分布是Beta分布的多元形式，自然的其也是多项分布的共轭先验分布。

共轭先验在Beta分布里面已经提到过，目前笔者也只是稍微了解了一点，后面笔者也打算专门去深入了解一下。

狄利克雷分布可以用来定义“不确定性”的问题。考虑一个3面骰子。如果我们知道每个结果都是等可能的，我们可以使用“尖峰”对称狄利克雷，如Dir(20,20,20)，即我们确信结果将是不可预测的。相比之下，如果我们不确定结果会是什么样子(例如，它可能是一个有偏的骰子)，那么我们可以使用“平坦”对称狄利克雷，例如Dir(1,1,1)，它可以生成广泛的可能的结果分布。

三、高斯联合分布

实践中最广泛使用的连续随机变量联合概率分布是多元高斯分布了，也叫多元正态分布(MVN)。这部分是因为其在数学上很方便，而且高斯分布假设在许多情况下是相当合理的。

1. The multivariate normal

定义

多元高斯分布的定义应该都很熟悉了：

可以对协方差矩阵进行限制：

Gaussian shells

随着维度$D$的增加，样本$x∼N(0,I_D)$中大部分点并不位于原点附近，而是集中在距离原点$r = \sqrt{D}$​ 处的一个薄壳或环形区域。这是因为虽然概率密度随着$\frac{r^2}{2}$指数衰减（距离增大概率密度减小），但球体的体积 随距离增加而增加，导致大多数点集中在距离原点$\sqrt{D}$处的一个薄环上。此现象称为“高斯肥皂泡”。

计算点$x$到原点的平方距离$d(x) = \sum_{i=1}^{D} x_i^2$​，其中$x_i \sim N(0, 1)$。

• 期望值：$\mathbb{E}[d^2] = D$。
• 方差：$\text{Var}(d^2) = D$。

所以随着D的增大，the coefficient of variation（标准差与期望的比值）会趋近于0

Marginals and conditionals of an MVN

对于一个满足多元高斯分布的向量$x$进行分块为$x1，x2$，会发现其边缘分布均为高斯分布，条件分布也均为高斯分布。

并且$p(x_1|x_2)$的后验均值是$x_2$的线性函数，但协方差于$x_2$无关，这是高斯分布的一个特殊性质。具体如下：

其它表达形式

高斯分布有其它表达形式，这些形式有对应的优势，例如边缘化公式在矩形式下更简单，而条件化公式在信息形式下更简单

2. Linear Gaussian systems

线性高斯系统定义如下，一个变量$z$和条件分布$p(y|z)$均为高斯分布：

此时联合分布$p(z,y)$的形式如下：

而后验分布$p(z|y)$也是一个高斯分布：

四、The exponential family

指数族包括了众多上面提到的常见分布，比如高斯分布、二项分布、多项式分布、 泊松分布、gamma分布、beta分布等等。

其在机器学习里面起着至关重要的作用，主要因为其独特的优点：

1. 定义

指数族分布（Exponential Family Distribution）： 指数族分布是一类可以写成如下形式的分布：
$$p(x|\eta) = h(x) \exp \left( \eta^T T(x) - A(\eta) \right)$$
其中，$\eta$是自然参数，$T(x)$是充分统计量，$A(\eta)$是归一化常数，确保概率分布的积分为1。具体定义如下：

在数族分布中，如果自然参数$\eta$之间相互独立，则可以更方便地进行推导和计算。所谓的独立性意味着没有非零的$\eta$满足$\eta^T T(x) = 0$，即自然参数$\eta$不能通过其他参数线性组合来为零。此时我们称一个指数族分布为最小，因为这意味着我们不能通过减少自然参数的数量来进一步简化分布的参数化，否则分布会变得冗余。

在多项式分布中，由于参数有一个和为1的约束条件，导致自然参数之间并不完全独立。因此，严格来说，多项式分布并不是最小指数族。但尽管多项式分布中自然参数有依赖性，但可以通过重新参数化，将$K$个参数中的一个去掉，使用$K-1$个独立的参数来表示整个分布。这样可以将原来的问题转换为最小指数族的形式，使得参数之间更加独立。

2. 例子

2.1 伯努利分布：

$$\begin{align*} P(x|\mu) &=\mu^x(1-\mu)^{1-x} \&=exp (ln(\mu^x(1-\mu)^{1-x})) \&=exp(xln(\frac{\mu}{1-\mu})+ln(1-\mu)) \end{align*}$$

对比可知有如下关系:

• [规范参数]$\eta = \phi(\mu)=ln(\frac{\mu}{1-\mu})$
• [充分统计量]$T(x)=x$
• [累积函数]$A(\eta)=-ln(1-\mu)$
• [基础度量值]$h(x)=1$
  *$\lambda = logistic(\eta)=\frac{1}{1+e^{-\eta}}$

上面也提到了多项式分布怎么减少参数量（让参数变为互相独立的）。

2.2 Categorical distribution

与伯努利分布类似，由于参数求和为1，所以独立变量只有$K-1$个：

2.3 单变量高斯分布

高斯分布可做如下变换：

$$\begin{align*} P(x|\mu,\sigma^2)&=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2) \&=\frac{1}{\sqrt{2\pi}}exp(\frac{\mu}{\sigma^2}x-\frac{1}{2\sigma^2}x^2-\frac{1}{2\sigma^2}\mu^2-ln\sigma) \end{align*}$$

同样对比可知:

• [规范参数]$\eta = \phi(\lambda)=[\frac{\mu}{\sigma^2},-\frac{1}{2\sigma^2}]$
• [充分统计量]$T(x)=[x,x^2]$
• [累积函数]$A(\eta)=\frac{1}{2\sigma^2}\mu^2+ln\sigma$
• [基础度量值]$h(x)=\frac{1}{\sqrt{2\pi}}$
• 因为高斯模型有两个参数,所以两个向量长度都为2

如果限制$\sigma^{2} = 1$，则有如下形式：

此时$h(x)$不再是常数。

2.4 多元高斯分布

与单变量高斯分布推导类似，但比较复杂，如下所示：

2.5 不是指数族的例子

分布族为指数族的必要条件为它有共同支撑集，也即$S_\theta = {x: p(x) > 0}$与$\theta$无关。

比如说均匀分布$R(0, \theta)$就没有共同支撑集（因为它非零的区域为$[0,\theta]$），所以它不可能是指数族分布。

3. 重要性质

Log partition function

对数配分函数$A(\eta)$有如下性质：

直接从定义证明即可

自然参数和矩参数转换

对数分区函数$A(\eta)$的梯度等于充分统计量的期望，也就是矩参数（或均值参数）。即：$m = E[T(x)] = \nabla_\eta A(\eta)$这表明我们可以通过计算$A(\eta)$的梯度，从自然参数$\eta$得到对应的矩参数$m$。

如果指数族是最小的，则可以从矩参数$m$转换回自然参数$\eta$。这一过程通过对函数$A(\eta)$的凸共轭函数（convex conjugate）$A^(m)$实现，公式为：$\eta = \nabla_m A^(m)$

其中，凸共轭函数$A^(m)$定义为：$A^(m) = \sup_{\eta \in \Omega} \left( m^T \eta - A(\eta) \right)$这意味着通过$A^*$的梯度可以从矩参数$m$转回自然参数$\eta$。

4. 指数族的极大似然估计

指数族模型的似然函数形式：对于指数族分布模型，其似然函数可以写成以下形式：$p(D|\eta) = \prod_{n=1}^N h(x_n) \exp \left( \eta^T \sum_{n=1}^N T(x_n) - N A(\eta) \right)$

上式可以化简为：

$$p(D|\eta) \propto \exp \left( \eta^T T(D) - N A(\eta) \right)$$

这里$T(D)$是数据集的充分统计量之和：
$$T(D) = \left[ \sum_{n=1}^N T_1(x_n), \ldots, \sum_{n=1}^N T_K(x_n) \right]$$
不同的分布对应不同的充分统计量，例如：

• 对于Bernoulli分布，充分统计量$T(D)$为：$T(D) = \left[ \sum_n I(x_n = 1) \right]$
• 对于一维高斯分布，充分统计量$T(D)$为：$T(D) = \left[ \sum_n x_n, \sum_n x_n^2 \right]$

Pitman-Koopman-Darmois定理说明在某些正则条件下，指数族分布是唯一具有有限充分统计量的分布族。也就是说，在指数族分布中，充分统计量的个数不依赖于数据集的大小。

给定数据集$D$，指数族分布的对数似然函数为：
$$\log p(D|\eta) = \eta^T T(D) - N A(\eta) + \text{const}$$

由于$-A(\eta)$是自然参数$\eta$的凸函数，而$\eta^T T(D)$是线性函数，因此可以得出：对数似然函数是凸的，从而存在唯一的全局最大值。

我们对对数似然函数求导，导数如下：
$$\nabla_\eta \log p(D|\eta) = T(D) - N E[T(x)]$$

对于单个数据点$x$，导数为：
$$\nabla_\eta \log p(x|\eta) = T(x) - E[T(x)]$$

至于$E[T(x)]$，我们用数据集进行估计即可：
$$E[T(x)] = \frac{1}{N} \sum_{n=1}^N T(x_n)$$

五、随机变量之间的变换

1. 双射

双射的变换公式很熟悉了，主要就是涉及到雅可比矩阵行列式：

2. 蒙特卡罗近似

也很熟悉了，就是采样估计：

3. Probability integral transform

这个其实就是从均匀分布采样，然后通过逆映射进行计算，这样就相当于从原分布中进行采样了。也比较熟悉了：

六、 马尔可夫链

马尔可夫链涉及的知识比较多，书上讲的也都是比较基础的，本科课程也学习过。主要记录一下之前没见过的：

马尔可夫链的最大似然估计：

MAP estimation：解决数据稀疏的问题，引入了Dirichlet先验：

七、比较两个分布的相似度

1. f-散度

f散度是一个函数，这个函数用来衡量两个概率密度p和q的区别，也就是衡量这两个分布多么的相同或者不同。像$KL$散度和$JS$散度都是它的一种特例

f散度定义如下：

$${D_f}(\mathcal P_1|\mathcal P_2)=\int f (\frac{p_2(x)}{p_1(x)})\cdot p_1(x)\mathrm d x=\mathbb E_{x\sim\mathcal P_1}\left[f(\frac{p_2(x)}{p_1(x)})\right] \$$

$f()$就是不同的散度函数，$D_f$就是在f散度函数下，两个分布的差异。规定

*$f$是凸函数(为了用琴生不等式)
*$f ( 1 ) = 0$(如果两个分布一样，刚好公式=0)

下面给出一些常见的f-散度例子：

KL 散度

当$f( r ) = rlog( r )$时，f-散度变为 KL 散度，公式为：

$$D_{KL}(p || q) = \int p(x) \log \frac{p(x)}{q(x)} dx$$

α-散度 (Alpha Divergence)

当$f(x) = \frac{4}{1 - \alpha^2} (1 - x^{\frac{1+\alpha}{2}})$时，f-散度变为 α-散度，公式为：

$$D^\alpha_A (p || q) = \frac{4}{1 - \alpha^2} \left( 1 - \int p(x)^{\frac{1+\alpha}{2}} q(x)^{\frac{1-\alpha}{2}} dx \right)$$

其中，$\alpha \neq \pm 1$。另一种常用的参数化方式（Minka 方式）为：

$$DD^\alpha_M(p || q) = \frac{1}{\alpha(1-\alpha)} \left( 1 - \int p(x)^\alpha q(x)^{1-\alpha} dx \right)$$

• 当$\alpha \to 0$时，α-散度趋向于$D_{KL}(q||p)$。
• 当$\alpha \to 1$时，α-散度趋向于$D_{KL}(p||q)$。
• 当$\alpha = 0.5$时，α-散度等于 Hellinger 距离（见下）。

Hellinger 距离 (Hellinger Distance)

平方的 Hellinger 距离定义为：

$$D_H^2(p || q) = \frac{1}{2} \int \left( \sqrt{p(x)} - \sqrt{q(x)} \right)^2 dx$$

这相当于 f-散度，其中$f( r ) = (\sqrt{r} - 1)^2$。

卡方距离 (Chi-Squared Distance)

卡方距离定义为：

$$\chi^2(p || q) = \frac{1}{2} \int \frac{(q(x) - p(x))^2}{q(x)} dx$$

这对应于 f-散度，其中$f( r ) = ( r - 1 )^2$。

2. 积分概率度量 (Integral Probability Metrics, IPM)

IPM 也用于计算两个分布$P$和$Q$之间的差异，其定义为：

$$
D_F(P, Q) = \sup_{f \in F} \left| \mathbb{E}{p(x)}[f(x)] - \mathbb{E}{q(x’)}[f(x’)] \right|
$$

其中，$F$是一类“光滑”的函数。常见的 IPM 度量包括：

• 最大均值差异 (Maximum Mean Discrepancy, MMD)

如果$F$是在正定核函数下的 RKHS（再生核希尔伯特空间），则对应的 IPM 被称为最大均值差异（MMD）。

• Wasserstein 距离 (Wasserstein Distance)

如果$F$是满足 Lipschitz 条件的函数类$F = { ||f||_L \leq 1 }$，即 Lipschitz 常数有界（例如为1）的函数集合，则 IPM 变为 Wasserstein-1 距离：

$$
W_1(P, Q) = \sup_{||f||L \leq 1} \left| \mathbb{E}{p(x)}[f(x)] - \mathbb{E}_{q(x)}[f(x’)] \right|
$$