[Probabilistic Machine Learning]: Fundamentals-Statistics

本学习笔记用于记录我学习Probabilistic Machine Learning的学习笔记，分享记录，也便于自己实时查看。

前面Probability部分重点是关注给定参数$\theta$后，数据$D$的分布，即$P(D|\theta)$，而Statistics部分则是关注给定数据分布下，参数$\theta$的概率，即$P(\theta|D)$。

一、贝叶斯统计

贝叶斯统计也是比较熟悉了，主要就是用贝叶斯公式进行计算后验：

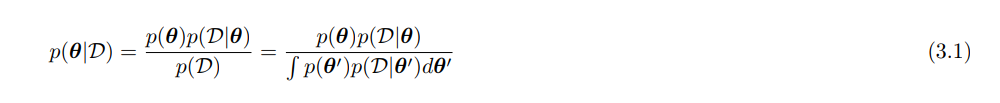
这里$P(\theta)$叫做先验，$P(\theta|D)$是后验，$P(D|\theta)$叫做似然。

书中以抛硬币实验来讲述了贝叶斯统计的众多概率，这里简单总结一下：

Prior ：均匀分布或者Beta分布，抛硬币我们可以选择Beta分布来指定更强的先验：
$$p(θ)=Beta(θ∣α,β)∝θ ^{α−1} (1−θ) ^{β−1}$$
Posterior：在Beta分布先验条件下可计算得到后验为：
$$p(θ∣D)∝θ^{N_1}(1−θ)^{N_0}⋅θ^{α−1}(1−θ)^{β−1}=Beta(θ∣α+N_1,β+N_0)$$
MAP 估计：即让后验最大
$$\hat{\theta}_{\text{MAP}} = \frac{\alpha + N_1 - 1}{\alpha + N_1 - 1 + \beta + N_0 - 1}$$
用均匀分布先验则和MLE得到的结果一致。
Posterior Mean：很多时候会使用后验的均值而非峰值作为参数，:
$$\hat{\theta} = \int \theta \cdot p(\theta|D) d\theta$$
Posterior Variance：表达估计的不确定性，对于抛硬币可得到标准差
$$\sigma = \sqrt{V[\theta|D]} \approx \sqrt{\frac{\hat{\theta}(1 - \hat{\theta})}{N}}$$
所以随着样本量$N$的增大，不确定性以$\frac{1}{\sqrt{N}}$ 的速度下降。不确定性（方差）在$\hat{\theta} = 0.5$时达到最大，在$\hatθ$接近0或1时达到最小。这表明，确定一个硬币偏向比确定它是公平的要容易得多。
Credible Intervals：置信区间，后验分布的 100(1 - α)% 置信区间定义
$$C_\alpha(D) = (l, u) : P(l \leq \theta \leq u|D) = 1 - \alpha$$
Posterior Predictive Distribution：假设我们希望预测未来的观测值，贝叶斯最优方法是通过边缘化未知参数来计算后验预测分布：
$$p(y|D) = \int p(y|\theta) p(\theta|D) d\theta$$
有时计算该积分可能会很困难，这时可以使用点估计方法，选择一个参数估计值$\hat{\theta} = \delta(D)$，例如 MLE 或 MAP，从而近似为：
$$p(y|D) \approx p(y|\hat{\theta})$$
Marginal Likelihood：对于优化没有影响，主要在于对模型的选择上：
$$p(D|M) = \int p(\theta|M) p(D|\theta, M) d\theta \quad$$

还提到了一个定理**de Finetti’s theorem（德·芬尼蒂定理）：**如果数据是可交换的，那么必然存在一个隐藏的随机变量$\theta$，数据在给定$\theta$的条件下是独立同分布的。这个定理为贝叶斯方法提供了理论基础。

二、频率学派统计

与贝叶斯统计不同，频率学派不将参数当作随机变量，而是依赖采样分布来表示不确定性。它通过反复采样来评估数据中的随机性和不确定性，而不是使用先验分布和后验分布。核心思想是重复实验的假设：通过观察如果在不同的数据集上重复实验，估计的量（例如参数）会如何变化，这种变化构成了不确定性的依据。

这个也很熟悉了，简单来说就是频率学派认为参数是一个值，通过不断地实验就能去估计这个值。虽然这个有一定的缺点，但其一些准则在实践中也是被广泛使用的。

1. Sampling distributions

采样分布是对某个估计器（如最大似然估计，MLE）的结果变化进行的描述。

举例来说，假设从一个真实模型$p(x|\theta^*)$中采样多个数据集$D^{(s)}$，然后对每个数据集应用估计器来得到参数估计$\hat{\theta}(D^{(s)})$。通过让数据集的数量$S$趋向无穷，我们可以得到估计器的采样分布。这个分布反映了在不同的样本下，参数估计的变化情况。

2. Bootstrap 自助法

当估计器比较复杂或者样本量较小的时候，可以使用Bootstrap方法来近似采样分布。自助法的核心是通过从原始数据集中随机采样生成多个伪数据集，然后计算每个伪数据集的参数估计，最终得到估计值的经验分布。主要有两种方法：

参数自助法假设我们知道参数$\theta^$，我们可以生成伪数据集并计算估计值。但现实是$\theta^$是未知的，所以我们使用从数据中估计出的参数$\hat{\theta}$，这就称为“参数自助法”。
另一种是非参数自助法，它不依赖于特定的生成模型，而是直接从原始数据集中进行有放回的采样，这样每个新生成的数据集与原始数据集有相同的大小，但通常会有重复数据点。

3. 渐近正态性（Asymptotic Normality）

当样本量足够大时，最大似然估计（MLE）的采样分布会趋向于正态分布。这称为MLE的渐近正态性。在数学上，它表述为：

$$\sqrt{N}(\hat{\theta} - \theta^) \rightarrow N(0, F(\theta^)^{-1})$$

Fisher 信息矩阵其中$F(\theta^*)$是费舍尔信息矩阵。

费舍尔信息矩阵衡量的是似然函数在真参数处的曲率，表明数据中包含的“信息量”。渐近正态性意味着，当样本量$N$趋于无穷时，估计值的分布会收敛于一个以真参数$\theta^*$为中心的高斯分布。

4. Fisher 信息矩阵

**Fisher 信息矩阵（Fisher Information Matrix, FIM）**与对数似然函数的曲率密切相关。这一矩阵在频率学派统计中有重要作用，主要用于刻画最大似然估计（MLE）的采样分布。此外，Fisher 信息矩阵在贝叶斯统计中也有应用，例如推导 Jeffreys 的无信息先验，以及在优化问题中作为自然梯度下降的一部分。

定义如下：

score function ：
$$s(\theta)\equiv\nabla_\theta\log p(x|\theta)$$

Fisher 信息矩阵 ：
$$F(\theta) \equiv \mathbb{E}{x \sim p(x|\theta)} \left[ \nabla\theta \log p(x|\theta) \nabla_\theta \log p(x|\theta)^T \right]$$

其第$i,j$项为：

$$F_{ij} = \mathbb{E}_{x \sim \theta} \left[ \frac{\partial}{\partial \theta_i} \log p(x|\theta) \frac{\partial}{\partial \theta_j} \log p(x|\theta) \right]$$

可以看到Fisher 信息矩阵与负对数似然函数（NLL, Negative Log Likelihood）有关系：

$$\text{NLL}(\theta) = - \log p(D|\theta)$$

我们有如下定理：

定理 4.1 如果$\log p(x|\theta)$是二阶可微的，并且在某些正则条件下，Fisher 信息矩阵等于 NLL 的期望 Hessian 矩阵：

$$
F(\theta){ij} = \mathbb{E}{x \sim \theta} \left[ \frac{\partial}{\partial \theta_i} \log p(x|\theta) \frac{\partial}{\partial \theta_j} \log p(x|\theta) \right] = - \mathbb{E}_{x \sim \theta} \left[ \frac{\partial^2}{\partial \theta_i \partial \theta_j} \log p(x|\theta) \right]
$$

然后书上给了一些常见分布的例子

二项分布的 FIM：$F(\theta) = \mathbb{E}_{x \sim \theta}[-s’(\theta|x)] = \frac{n}{\theta(1 - \theta)}$
单变量高斯分布的 FIM：$F(\theta) = \begin{pmatrix} \frac{1}{v} & 0 \ 0 & \frac{1}{2v^2} \end{pmatrix}$
逻辑回归的 FIM：$F(w) = \mathbb{E}{p(y|X,w,\lambda)}[\nabla^2 L(w)] = X^T \Lambda X + \lambda I$，其中$\Lambda{nn} = \sigma(w^T x_n)(1 - \sigma(w^T x_n))$。
指数族分布的 FIM：$F_\eta = \text{Cov}[T(x)]$

5. 频率学派的Counterintuitive properties

首先是**频率主义的置信区间，**它基于抽样分布来估计参数的不确定性。其定义是，如果重复抽取样本并计算每个样本的置信区间，那么有 95% 的区间会包含真实参数。但对于一个具体的样本，无法说参数有 95% 的概率落在置信区间内。换句话说，频率主义认为参数是固定的，数据是随机的，所以无法给出“参数在此区间的概率”。

贝叶斯方法则把数据固定，参数看作是随机的。因此，贝叶斯的可信区间给出了参数在某区间内的概率。这是人们在直觉上通常更关心的问题：已知数据后，参数落在某个范围的概率。

文中提到一个具体的例子：

然后就是**p 值的误导性，**p 值是指在原假设（H0）成立时，观察到某个统计量或更极端结果的概率。频率主义的假设检验通过计算 p 值来决定是否拒绝原假设，通常认为 p 值很小就意味着原假设不太可能成立。

问题是p 值经常被错误地解释为“原假设为真的概率”，但实际上它只是给出了在原假设成立的情况下，观察到数据的概率。它并没有告诉我们在看到数据后原假设是否成立，或者备择假设（H1）是否更有可能成立。

文中用了一个类比来说明 p 值的误导性。假设“如果一个人是美国人，他大概率不是国会议员”，我们观测到某人是国会议员，但这并不能推导出“这个人很可能不是美国人”。

这是一个典型的错误推理，类似于依赖 p 值来判断假设的真实性。相反，贝叶斯方法会使用贝叶斯定理结合数据推导出假设的后验概率，更符合人们的直觉。

三、共轭先验

如果先验分布$p(\theta)$属于某个参数化家族$F$，并且后验分布$p(\theta|D)$也在该家族中，则称$p(\theta)$为$p(D|\theta)$的共轭先验。这意味着贝叶斯更新后，分布保持在同一个家族中，便于计算。

书中详细介绍了常见分布的共轭先验，这里仅做总结：

3.1 二项分布

**共轭先验：**贝塔分布
$$p(\theta) = \text{Beta}(\theta | \alpha, \beta)$$
**更新公式：**在观察到$k$次成功和$n$次试验后，后验分布为：
$$p(\theta | k, n) = \text{Beta}(\theta | \alpha + k, \beta + n - k)$$

3.2. 多类分布

**共轭先验：**狄利克雷分布：
$$p(\boldsymbol{\theta}) = \text{Dirichlet}(\boldsymbol{\theta} | \boldsymbol{\alpha})$$
**更新公式：**如果观察到类别$i$的次数为$n_i$，则后验分布为
$$p(\boldsymbol{\theta} | \mathbf{n}) = \text{Dirichlet}(\boldsymbol{\theta} | \boldsymbol{\alpha} + \mathbf{n})$$

其中$\mathbf{n} = (n_1, n_2, \ldots, n_k)$表示每个类别的观察次数。

3.3 单变量高斯模型（Univariate Gaussian Model）

3.3.1 给定$\sigma^2$的后验

**共轭先验：**另一个高斯分布：
$$N(\mu|m_0, \tau_0^2)$$
**更新公式：**后验分布也为高斯分布，参数为：
$$
\begin{align}
\hat{\tau}^2 &= \frac{1}{\frac{1}{\sigma^2} + \frac{N}{\tau_0^2}} \
\hat{m} &= \hat{\tau}^2 \left( \frac{m_0}{\tau_0^2} + \frac{N\bar{y}}{\sigma^2} \right)
\end{align}
$$
这里，$\bar{y}$是样本均值。

3.3.2 给定$μ$的后验

共轭先验为逆伽马分布：
$$\text{IG}(\sigma^2|\alpha_0, \beta_0) \propto (\sigma^2)^{-\alpha_0 - 1} \exp\left(-\frac{\beta_0}{\sigma^2}\right)$$
**更新公式：**后验分布也是逆伽马分布，参数为：
$$
\begin{align}
&\hat{\alpha} = \alpha_0 + \frac{N}{2} \
&\hat{\beta} = \beta_0 + \frac{1}{2}\sum_{n=1}^{N}(y_n - \mu)^2
\end{align}
$$

3.3.3 对于均值$\mu$和方差$\sigma^2$的推断

**共轭先验：**正态-逆伽马分布（NIG）：
$$NIG(\mu, \sigma^2 | m, \kappa, a, b) \equiv N(\mu | m, \frac{\sigma^2}{\kappa}) IG(\sigma^2 | a, b)$$
一般就用正态-逆卡方分布（NIX）：
$$NI\chi^2(\mu, \sigma^2 | m, \kappa, \nu, \tau^2) \equiv N(\mu | m, \frac{\sigma^2}{\kappa}) \chi^{-2}(\sigma^2 | \nu, \tau^2)$$
**更新公式：**后验参数更新：
$$
\begin{align}
&\hat{m} = \frac{\kappa m + N\hat{x}}{\hat{\kappa}} \
&\hat{\kappa} = \kappa + N \
&\hat{\nu} = \nu + N \
&\hat{\nu} \hat{\tau}^2 = \nu \tau^2 + \sum_{n=1}^{N}(y_n - \bar{y})^2 + \frac{N\kappa}{\kappa + N}(m - \bar{y})^2
\end{align}
$$
方差的后验边际分布：
$$p(\sigma^2 | D) = \chi^{-2}(\sigma^2 | \hat{\nu}, \hat{\tau}^2)$$
均值的后验边际分布：
$$p(\mu | D) = T(\mu | \hat{m}, \frac{\hat{\tau}^2}{\hat{\kappa}}, \hat{\nu})$$

3.4. 对于多变量高斯模型

3.4.1 在给定 Σ 的情况下推断 µ

**共轭先验：**高斯分布:
$$p(\mu) = N(\mu | m, V)$$
后验分布： :
$$p(\mu | D, \Sigma) = N(\mu | \hat{m}, \hat{V})$$
更新公式：
$$
\begin{align}
&\hat{V}^{-1} = V^{-1} + N\Sigma^{-1} \
&\hat{m} = \hat{V}(\Sigma^{-1}(Ny) + V^{-1}m)
\end{align}
$$

3.4.2 在给定 µ 的情况下推断 Σ

**共轭先验：**逆Wishart分布:
$$p(\Sigma) = IW(\Sigma | \Psi^{-1}, \nu)$$
后验分布： :
$$p(\Sigma | D, \mu) \propto IW(\Sigma | \hat{\Psi}, \hat{\nu})$$
更新公式：
$$
\begin{align}
&\hat{\nu} = \nu + N\
&\hat{\Psi} = \Psi + S_\mu
\end{align}
$$

3.4.3 同时推断 Σ 和 µ

共轭先验：
$$p(\mu, \Sigma) = N(\mu | m, V) IW(\Sigma | \Psi^{-1}, \nu)$$
后验分布：
$$p(\mu, \Sigma | D) \propto |\Sigma|^{-\frac{N + \nu + D + 2}{2}} \exp\left(-\frac{1}{2} \text{tr}(\Sigma^{-1} M)\right)$$
其中$M$是更新后的散点矩阵。

3.5 指数族模型

唯一存在共轭先验的分布族是指数族，具体如下：

**共轭先验：**我们可以将先验分布写成与似然函数相似的形式：
$$p(\eta|\tilde{\tau}, \tilde{\nu}) = \frac{1}{Z(\tilde{\tau}, \tilde{\nu})} \exp\left(\tilde{\tau}^T \eta - \tilde{\nu} A(\eta)\right)$$
其中，$\tilde{\nu}$是先验的强度，$\frac{\tilde{\tau}}{\tilde{\nu}}$ 是先验均值，$Z(\tilde{\tau}, \tilde{\nu})$是归一化因子。
后验分布：
$$
\begin{align}
p(\eta|D) &= \frac{p(D|\eta) p(\eta)}{p(D)} \
&= \frac{h(D)}{Z(\tilde{\tau}, \tilde{\nu})p(D)} \exp\left( (\tilde{\tau} + s(D))^T \eta - (\tilde{\nu} + N) A(\eta)\right) \
&= \frac{1}{Z(\hat{\tau}, \hat{\nu})} \exp\left(\hat{\tau}^T \eta - \hat{\nu} A(\eta)\right)
\end{align}
$$
其中：
$$
\begin{align}
&\hat{\tau} = \tilde{\tau} + s(D)\
&\hat{\nu} = \tilde{\nu} + N \
&Z(\hat{\tau}, \hat{\nu}) = \frac{Z(\tilde{\tau}, \tilde{\nu})h(D)}{p(D)}
\end{align}
$$

我们看到，后验分布与先验分布具有相同的形式，只是更新了充分统计量和样本大小。后验均值为先验均值与经验均值（即最大似然估计）之间的组合：

$$\begin{align*} E[\eta|D] &= \frac{\hat{\tau}}{\hat{\nu}} \
&= \frac{\tilde{\tau} + s(D)}{\tilde{\nu} + N} \
&= \frac{\tilde{\nu}}{\tilde{\nu} + N} \frac{\tilde{\tau}}{\tilde{\nu}} + \frac{N}{\tilde{\nu} + N} \frac{s(D)}{N} \
&= \lambda E[\eta] + (1 - \lambda) \hat{\eta}_{MLE} \end{align*}$$

其中，$\lambda = \frac{\tilde{\nu}}{\tilde{\nu} + N}$。

边际似然：
$$p(D) = \frac{Z(\hat{\tau}, \hat{\nu}) h(D)}{Z(\tilde{\tau}, \tilde{\nu})}$$
**后验预测密度：**我们现在推导给定过去数据$D = (x_1, …, x_N)$时，未来观测$D’ = (x’1, …, x’{N’})$的预测密度，如下：

$$\begin{align*} p(D’|D) &= \int p(D’|\eta) p(\eta|D) d\eta \&=h(D’) \frac{Z(\tilde{\tau} + s(D) + s(D’), \tilde{\nu} + N + N’)}{Z(\tilde{\tau} + s(D), \tilde{\nu} + N)} \end{align*}$$

四、无信息先验

在缺乏领域特定知识时，我们不希望主观定义不合理的先验，于是我们便可以选择无信息先验客观。主要有如下几种：

1. 最大熵先验（Maximum entropy priors）

最大熵先验是一种不做过多假设的先验分布，适合在没有充足信息的情况下使用。通过最大化熵来选择先验，这种方法依赖于拉普拉斯提出的“不充分理由原则”，即当我们没有理由偏向某个特定值时，应选择“平坦”的分布。例如，对于伯努利分布的参数 θ（取值范围 [0,1]），最大熵先验是均匀分布。

我们也可以根据已知约束来定义最大熵先验，使其在满足这些约束的同时使得熵最大化。书中举了一个例子：

2. 杰弗里斯先验（Jeffreys priors）

Jeffreys priors通过保证对参数化不敏感，即在不同的参数化方式下，后验分布不会改变。杰弗里斯先验的一个关键特性是对参数的变化保持不变，这意味着无论采用何种参数化方式，结果应该是一致的。

参数$\theta$的 Jeffreys Prior 为以下形式：

$$p_{J}(\theta) \propto \sqrt{\mathcal{I}(\theta)}$$

其中，$\mathcal{I}(\theta)$是我们所熟知的Fisher信息量。证明如下：

例如对于伯努利分布，其杰弗里斯先验是 Beta(1/2, 1/2) 分布。

3. 不变性先验（Invariant priors）

不变性先验是指当我们知道某些不变性时，可以将其编码进先验中。例如：

平移不变先验：对位置参数的推断可以使用平移不变先验，这种先验在任何相同宽度的区间上都分配相同的概率质量。

尺度不变先验：对尺度参数的推断可以使用尺度不变先验，其满足任意比例缩放后保持相同概率质量。

4. 参考先验（Reference priors）

参考先验通过最大化数据集上的后验与先验之间的KL散度来定义。它旨在使先验尽可能远离所有可能的后验分布，从而保持非信息性。参考先验可以看作是对不同数据集的互信息最大化问题。对于一维情况，参考先验等同于Jeffreys priors，而在高维情况下，计算起来则更复杂。

五、层次先验（Hierarchical priors）

贝叶斯模型需要为参数$\theta$指定先验$p(\theta)$，而先验的参数（超参数$\xi$）也是未知的。为了处理这种不确定性，我们可以对超参数$\xi$再定义一个先验，从而构建层次贝叶斯模型。这种模型的形式化表达为：$p(\xi, \theta, D) = p(\xi) p(\theta | \xi) p(D | \theta)$

这表明数据$D$通过参数$\theta$依赖于超参数$\xi$，从而形成一个层次结构。

在实际问题中，如果我们有多个相关的数据集$D_j$，各个数据集有自己的参数$\theta_j$，那么分别独立估计每个$\theta_j$ 可能会产生不可靠的结果，特别是当某个数据集较小时。层次模型可以通过共享超参数$\xi$来借用数据量大的群体的信息，帮助数据量小的群体进行更好的估计.

1. 层次二项模型的例子

问题背景：假设我们想估计不同群体中某种疾病的患病率，每个群体的样本量是$N_j$，阳性病例数是$y_j$。我们可以假设$y_j$服从二项分布$\text{Bin}(N_j, \theta_j)$，其中$\theta_j$ 是该群体的患病率。

如果直接对每个群体单独估计$\theta_j$，特别是当样本量$N_j$很小时，可能会导致不可靠的结果。比如，如果$y_j = 0$，我们可能会估计$\hat{\theta_j} = 0$，尽管实际的患病率可能更高。

解决方案：为了避免这种问题，可以假设所有的$\theta_j$不是独立的，而是从一个共同的 Beta 分布中抽取，即$\theta_j \sim \text{Beta}(a, b)$。这个假设允许我们通过共享的先验$\xi = (a, b)$来提高估计的可靠性。这种模型的联合分布可以写作：
$$p(D, \theta, \xi) = p(\xi) \prod_{j=1}^{J} \text{Beta}(\theta_j | \xi) \prod_{j=1}^{J} \text{Bin}(y_j | N_j, \theta_j)$$

后验推断：可以通过Hamiltonian Monte Carlo（HMC）算法来进行后验推断，生成超参数$\xi$和群体参数$\theta_j$ 的样本。对于每个群体，后验均值$E[\theta_j | D]$会根据数据量的大小进行调整。对于数据较少的群体，估计值会向全体群体的均值（共享信息）靠拢，这种现象被称为收缩（shrinkage）。

2. 层次高斯模型的例子

问题背景：现在考虑实数值数据的情况，假设我们有多个群体的数据，每个群体的数据$y_{ij}$服从正态分布$N(\theta_j, \sigma^2)$，其中$\theta_j$ 是该群体的均值，$\sigma^2$是固定的方差。

与二项模型类似，我们可以假设各群体的均值$\theta_j$ 来自一个共同的正态分布$\theta_j \sim N(\mu, \tau^2)$。这个模型的联合分布为：
$$p\propto p(\mu)p(\tau^2) \prod_{j=1}^{J} N(\theta_j | \mu, \tau^2) N(y_j | \theta_j, \sigma_j^2)$$

其中$p(\mu)$和$p(\tau^2)$是超参数的先验分布，可以假定$\sigma_j^2$是知道的。

对于每个群体，后验均值$E[\theta_j | D]$会介于单独的最大似然估计值$\hat{\theta_j}$和全局均值$\mu$之间。根据公式：
$$E[\theta_j | D, \mu, \tau^2] = w_j \mu + (1 - w_j) \hat{\theta_j}$$

其中收缩系数$w_j = \frac{\sigma_j^2}{\sigma_j^2 + \tau^2}$。数据量较小或不确定性较高的群体（即$\sigma_j^2$较大的群体）会有更大的收缩，意味着它们的估计值会更多地依赖于全局均值。

为了解决算法在进行后验推断时的计算效率问题，可以采用非中心化参数化（non-centered parameterization）。这种方法通过重新表达$\theta_j = \mu + \tau \eta_j$，其中$\eta_j \sim N(0, 1)$，从而减少参数之间的依赖性，提升推断的计算效率。

六、经验贝叶斯

对于层次贝叶斯模型，在全贝叶斯推断中，我们对底层参数和超参数同时进行推断，计算$p(\theta, \xi | D)$的联合后验分布。虽然这种方法在统计上是更为严格的，但计算量通常较大。经验贝叶斯提供了一种近似方法，首先通过最大化边际似然（如$p(D|\xi)$）估计超参数$\xi$，然后在给定这些估计值的条件下推断底层参数的后验分布（如$p(\theta|\hat{\xi}, D)$）。这种方法通过对超参数做点估计，而非推断它们的后验分布，因此简化了计算。

通过边际似然最大化来估计超参数是经验贝叶斯的核心步骤。具体来说，经验贝叶斯在给定数据$D$的条件下，通过最大化边际似然$p(D|\xi)$来找到最优的超参数估计值$\hat{\xi}$。这种方法有时也被称为II类最大似然，因为它不是直接优化底层参数$\theta$，而是先优化超参数$\xi$。

1. 经验贝叶斯在层次二项模型中的应用

在二项分布的层次模型中，经验贝叶斯的边际似然可以通过积分将底层参数$\theta_j$ 消除掉，从而直接用超参数$\xi$表示边际似然。具体公式是：

$$p(D|\xi) = \prod_j \int \text{Bin}(y_j|N_j, \theta_j) \text{Beta}(\theta_j | a, b) d\theta_j$$

经验贝叶斯方法通过最大化此边际似然来估计超参数$a$和$b$，然后在给定这些估计值后，再计算每个$\theta_j$的后验分布。

2. 经验贝叶斯在层次高斯模型中的应用

在层次高斯模型中，经验贝叶斯可以通过边际化$\theta_j$ 得到边际似然，并利用最大似然估计超参数$\mu$和$\tau^2$。在这个例子中，边际似然公式是：

$$p(D|\mu, \tau^2, \sigma^2) = \prod_{j=1}^{J} N(y_j | \mu, \tau^2 + \sigma^2)$$

然后通过矩匹配方法估计$\tau^2$和$\mu$。

3. 经验贝叶斯在马尔可夫模型中的应用

经验贝叶斯还可以用于语言模型中的 n-gram 平滑问题。在这个上下文中，经验贝叶斯被用来估计马尔可夫链中状态转移矩阵的先验分布。通过为转移矩阵的每一行设定一个独立的狄利克雷分布作为先验，经验贝叶斯可以通过最大化边际似然来估计先验参数$\alpha$和$m$，从而得到自适应的平滑方法。这个方法的优势在于，它能够根据数据自动调整平滑参数$\lambda_j$，从而提高模型的表现。

在 n-gram 语言模型中，我们希望计算不同词之间的转移概率，比如在二元模型（bigram model）中，给定词$X_t = j$，下一个词$X_{t+1} = k$的概率可以由转移矩阵$A_{jk}$ 来表示。传统的加一平滑方法对每一个可能的词对$(j, k)$都假设了一个等价的概率，但这种假设往往过于简单。**删除插值（deleted interpolation）**是一个更复杂的方案，定义了如下的转移矩阵表示：

$$A_{jk} = (1 - \lambda) f_{jk} + \lambda f_k$$

其中，$f_{jk} = \frac{N_{jk}}{N_j}$是从词$j$到词$k$的 bigram 频率，$f_k = \frac{N_k}{N}$ 是词$k$的 unigram 频率，而$\lambda$是一个通过交叉验证选择的平滑参数。

然而，删除插值方法没有考虑不同的上下文在词的频率中可能有不同的重要性。贝叶斯方法则可以为每个上下文动态地调整平滑参数$\lambda_j$。

通过经验贝叶斯的方法对删除插值进行了重新解释。首先，假设转移矩阵的每一行都遵循独立的 Dirichlet 先验分布：

$$A_j \sim Dir(\alpha_0 m_1, \dots, \alpha_0 m_K) = Dir(\alpha_0 m) = Dir(\alpha)$$

其中，$A_j$是转移矩阵的第$j$行，$m$是先验均值向量，满足$\sum_k m_k = 1$，而$\alpha_0$ 是先验强度。通过贝叶斯推断，可以得到转移矩阵行$A_j$的后验分布：

$$A_j \sim Dir(\alpha + N_j)$$

其中$N_j = (N_{j1}, \dots, N_{jK})$是从状态$j$转移到其他状态的计数向量。在此基础上，后验预测密度为：

$$p(X_{t+1} = k | X_t = j, D) = \frac{N_{jk} + \alpha_j m_k}{N_j + \alpha_0}$$

这个公式可以改写为删除插值的形式：

$$p(X_{t+1} = k | X_t = j, D) = (1 - \lambda_j) f_{jk} + \lambda_j m_k$$

其中，$\lambda_j = \frac{\alpha_j}{N_j + \alpha_0}$是动态调整的平滑参数，表示给定上下文$j$时，将先验分布与经验数据相结合的权重。

EB 方法的核心思想是通过数据来估计 Dirichlet 分布的超参数$\alpha$和$m$。在这个问题中，有一种近似方法来估计先验均值$m$：

$$m_k \propto |{ j : N_{jk} > 0 }|$$

这个估计意味着某个词$k$的先验概率与该词出现在多少种不同的上下文中有关，而不是它的具体出现次数。这种估计方法可以解决某些平滑方法中的不足。举个例子，如果在一个数据集中“you see”频繁出现，那么虽然 “you” 和 “see” 的 unigram 频率相同，但是它们在新上下文中出现的概率不应该相等。贝叶斯模型通过先验分布的参数$m_k$ 可以自适应地处理这种情况。

七、模型选择

在统计建模中，选择合适的模型至关重要。所有模型都存在一定的误差，然而某些模型能更好地适应数据，提供有用的预测。选择模型时，我们需要考虑模型的假设和拟合能力，确保它能在现实世界中应用。

1. 贝叶斯模型选择

贝叶斯模型选择的一个自然的想法是利用后验概率来确定最有可能生成数据的模型。公式如下：

$$\hat{m} = \arg\max_{m \in M} p(m|D)$$

这里的$p(m|D)$表示给定数据$D$下模型$m$的后验概率。根据贝叶斯定理，我们可以表示为：

$$p(m|D) = \frac{p(D|m)p(m)}{\sum_{m \in M} p(D|m)p(m)}$$

如果模型的先验是均匀的，即$p(m) = \frac{1}{|M|}$，那么最大后验模型是：

$$\hat{m} = \arg\max_{m \in M} p(D|m)$$

但是不同的模型设计是有好坏之分的。

示例：硬币是否公平？

假设我们想知道某个硬币是否是公平的。我们可以设定两个模型：

$M_0$：假设硬币是公平的，即$\theta = 0.5$。

$M_1$：假设硬币是偏向的，即$\theta$可以是任意值。

通过比较这两个模型的边际似然，我们可以决定哪个模型更有可能解释观察到的数据。例如：

在公平硬币模型下，观察到$N$次投掷的边际似然是：

$$p(D|M_0) = \left( \frac{1}{2} \right)^N$$

在偏向硬币模型下，边际似然更复杂，需要计算贝塔分布的积分：

$$p(D|M_1) = \int p(D|\theta)p(\theta|M_1)d\theta$$

如果观察到的正面次数较多，模型$M_1$ 的可能性会更高。可能说明$M_0$的先验并不好。

2. 贝叶斯模型平均

如果我们的目标是进行准确的预测，综合所有模型的预测结果通常比只依赖单一模型更好。贝叶斯模型平均可以表示为：

$$p(y|D) = \sum_{m \in M} p(y|m)p(m|D)$$
这里$p(y|m)$是模型$m$对新数据$y$的预测。通过对所有模型的预测进行加权平均，我们可以得到更稳健的结果。

与机器学习中的集成技术类似，我们取预测器的加权组合。然而，集成的权重不必总和为 1，尤其是在贝叶斯模型平均中，如果有一个最佳模型$m^$，在大样本极限下，$p(m|D)$将成为一个在$m^$上的退化分布，其他模型将被忽略。

3 边际似然估计

为了进行贝叶斯模型选择，我们需要计算在给定先验的条件下的边际似然：

$$p(D|m) = \int p(D|\theta, m)p(\theta|m)d\theta$$

这里的积分通常难以直接计算。对于共轭先验模型，边际似然可以解析计算，这类模型因其先验与后验分布形式一致，使得边际似然的计算变得简单明了。

但对于其它的，我们可以使用变分推断或蒙特卡洛方法来估计。文中还给了一个Harmonic mean estimator的方法：

4. 交叉验证与边际似然的联系

交叉验证是一种评估模型预测能力的常用方法。它通过将数据划分为训练集和验证集来评估模型的表现。**留一交叉验证（LOO-CV）**是一种特殊的情况，其中每次留出一个样本进行测试，其他样本用于训练。

交叉验证的结果可以用来估计模型的泛化能力。

它与**对数边际似然（LML）**有很一定的关系：

5. 条件边际似然

边际似然用于回答“从先验生成训练数据的可能性有多大？”。它适用于在不同的固定先验之间进行假设检验，但很多时候我们更关心的是“后验能够生成数据分布中的新样本的概率是多少？”，这与模型的泛化性能相关联。

研究表明，边际似然有时可能与模型的泛化性能负相关。这是因为边际似然可能会出现先验较差但模型快速适应数据的情况

为了解决这个问题，研究者们提出了条件对数边际似然（CLML），公式为：

$$CLML(m) = \sum_{n=K}^{N} \log p(D_n|D_{1:n-1}, m)$$

其中，$K \in {1, \dots, N}$是算法的一个参数。CLML通过给定前$K$个数据点的后验分布来评估后续$N - K$个数据点的边际似然。这种方法减少了数据点顺序对结果的依赖。特别地，当$K = N - 1$并对所有数据顺序进行平均时，这种方法相当于留一法（LOO）估计。

6. 贝叶斯留一法估计

对于监督模型来说，一个我们关注的点是**ELPD（expected log-pointwise predictive density），**ELPD 是对未来数据的预测性能进行估计的度量：

$$ELPD(m) = \mathbb{E}_{(x^, y^)} \left[ \log p(y^|x^, D, m) \right]$$

由于未来数据未知，因此可以使用 LOO 近似，即将部分数据点从数据集中移除并计算其预测分布：

$$ELPD_{\text{LOO}}(m) = \sum_{n=1}^N \log p(y_n|x_n, D_{-n}, m)$$

直接计算$ELPD_{\text{LOO}}$ 需要计算$N$次不同的后验分布，这比较慢。可以通过只计算一次后验分布$p(\theta|D, m)$，然后使用重要性采样近似 LOO 积分。

重要性采样的核心思想是定义目标分布$f(\theta) = p(\theta|D_{-n}, m)$，并使用已知的提议分布$g(\theta) = p(\theta|D, m)$，计算重要性权重：

$$w_{s,-n} = \frac{f(\theta_s)}{g(\theta_s)} \propto \frac{1}{p(D_n|\theta_s)}$$

将这些权重进行归一化后，可以用来近似 LOO 估计：

$$ELPD_{\text{IS-LOO}}(m) = \sum_{n=1}^N \log \sum_{s=1}^S \hat{w}_{s,-n} p(y_n|x_n, \theta_s, m)$$

重要性采样的一个问题是，权重的方差可能非常大，导致一些权重值过大。为了解决这个问题，可以对每个样本的权重拟合一个 Pareto 分布，从而对权重进行平滑。这样可以减少异常值对 LOO 估计的影响。

八、模型检测与假设检验

1. 后验预测检查（Posterior Predictive Checks）：

通过已知数据和模型生成未来的合成数据，以评估真实数据与模型生成的数据是否相似。如果模型生成的数据与真实数据差异很大，说明模型无法捕捉数据中的某些特征，模型可能不适合。

2.贝叶斯p值

通过计算贝叶斯p值来量化模型的合理性。如果观测到的测试统计量位于预测分布的极端部分（即p值接近0或1），说明模型无法合理解释数据

3. 假设检验

与频率学派的假设检验相对，贝叶斯方法提供了假设检验的两种替代方案：

使用贝叶斯因子进行模型比较：贝叶斯假设检验不再将检验统计量与临界值进行比较，而是评估在两种模型下数据的边际似然比——零假设$M_0$ 和替代假设$M_1$。这个比值称为贝叶斯因子，表示为：
$B_{1,0} = \frac{p(D | M_1)}{p(D | M_0)}$如果$B_{1,0} > 1$，我们倾向于支持$M_1$，否则我们更倾向于支持$M_0$。