[Probabilistic Machine Learning]: Fundamentals-Graphical models

概率图是随机变量集合的一种表现形式。在概率图中，节点代表随机变量，边的有无则表示这些变量之间的条件独立性假设。所以，称为“独立性图”似乎更为合适。根据图的不同类型，概率图模型可以分为有向图、无向图或有向无向混合图的模型。

一、有向图模型（贝叶斯网络）

基于有向无环图（DAGs）的有向概率图模型（DPGM）通常被称为贝叶斯网络（Bayes nets）。不过这里的“贝叶斯”其实只是定义概率分布的一种方法。

1. 联合分布的表示

DAG的一个关键特性是必定存在拓扑排序。根据拓扑排序的顺序，我们可以看成一个有序马尔可夫链，即一个节点在给定其父节点的情况下，与拓扑顺序中的所有前驱节点条件独立。公式如下：

\[x_i \perp x_{pred(i)\backslash pa(i)} | x_{pa(i)}\]

其中，\(pa(i)\)是节点\(i\)的父节点，而\(pred(i)\)是拓扑顺序中节点\(i\)的前驱节点。因此，联合分布可以如下表示（假设我们使用节点顺序 1 到\(N_G\)）：

\[p(x_{1:N_G}) = p(x_1) p(x_2|x_1) p(x_3|x_1, x_2) ... p(x_{N_G} | x_1, ..., x_{N_G-1}) = \prod_{i=1}^{N_G} p(x_i|x_{pa(i)})\]

其中，\(p(x_i|x_{pa(i)})\)是节点 i 的条件概率分布（CPD）。这种表示的主要优点是，由于图中编码的条件独立性假设，定义联合分布所需的参数数量可以大大减少。对于离散随机变量，未结构化的联合分布需要 \(O(K^{N_G})\) 个参数，而DAG中每个节点最多有\(N_P\)个父节点，仅需要 O(\(N_G*K^{(N_P+1)}\)) 个参数。如果DAG是稀疏的，这个数量会显著减少。

2. 例子

书中给了马尔科夫链的例子来具体说明。

显然二阶马尔科夫链也是一种有向图模型：

书中还给了"student" network和Sigmoid belief nets的例子。

Sigmoid belief nets其实就是一种潜变量的生成模型

3. 高斯贝叶斯网络（Gaussian Bayes Nets）

高斯贝叶斯网络（Gaussian Bayes Nets）也是一种有向概率图模型，其中所有的变量都是连续实值的，并且条件概率分布（CPD）具有线性高斯形式。具体来说，CPD 的形式如下：

\[p(x_i|x_{\text{pa}(i)}) = \mathcal{N}(x_i|\mu_i + w_i^T x_{\text{pa}(i)}, \sigma_i^2)\]

这表示每个变量\(x_i\)在给定它的父节点\(x_{\text{pa}(i)}\)的条件下，服从一个正态分布，其均值是父节点的线性组合加上一个局部均值\(\mu_i\)，标准差为\(\sigma_i\)​。

通过将这些局部 CPD 乘起来，我们可以得到一个大的联合高斯分布\(p(x) = \mathcal{N}(x|\mu, \Sigma)\)，其中\(x \in \mathbb{R}^{N_G}\)​ 表示所有变量的联合分布。最终，通过推导，我们得到整体均值向量\(\mu = (\mu_1, \mu_2, \dots, \mu_{N_G})\)是所有局部均值的拼接。而协方差则\(\Sigma = U S^2 U^T\)。其中\(S^2\)是标准差对角矩阵的平方。

具体过程如下：

4. 条件独立性（Conditional Independence, CI）

本部分首先定义了条件独立性(CI)的基本概念。\(x_A ⊥_G x_B|x_C\)表示在图\(G\)中，\(A\)与\(B\)在给定\(C\)的情况下是条件独立的。图\(G\)中的条件独立性陈述集合记为\(I(G)\)，而在某个分布\(p\)中成立的所有条件独立性陈述集合记为\(I(p)\)。

• 图\(G\)被称为分布\(p\)的I-map（独立性图）或分布\(p\)相对于\(G\)是马尔科夫的（Markov wrt G），当且仅当图G中的所有条件独立性陈述都成立于\(p\)中（即\(I(G) ⊆ I(p)\)）。这意味着图\(G\)可以作为分布\(p\)的代理，帮助我们推理\(p\)的条件独立性属性。 *\(G\)是\(p\)的最小I-map，当且仅当没有比\(G\)更小的图\(G′\)可以满足\(I(G') ⊆ I(p)\)。

4.1 全局马尔科夫性质 (d-separation)

接下来介绍了如何从有向无环图（DAG）中推导出条件独立性（CI）的概念，具体通过d-分离（d-separation）的方式实现。

• d-分离的定义： 对于一条无向路径P，如果以下任意条件之一成立，则P被节点集C（观测集）d-分离：

1. P包含链式结构：\(s → m → t\)或\(s ← m ← t\)，并且中间节点m属于C。
2. P包含分叉结构：\(s ↙m↘ t\)，并且中间节点m属于C。
3. P包含碰撞结构（v-结构）：\(s ↘m↙ t\)，并且中间节点m不属于C，且m的后代节点也不在C中。

如果对于任意\(a∈A\)和\(b∈B\)的所有无向路径都被\(C\)d-分离，则称节点集A与B在给定C的条件下是d-分离的。

• 全局马尔科夫性质： 当A与B在给定C的情况下是d-分离时，我们把这种条件独立性写为\(X_A ⊥_G X_B|X_C\)。这个性质也称为有向全局马尔科夫性质，用于判定图中的条件独立性。

具体为什么者三种情况成立，解释如下：

• \(X \rightarrow Y \rightarrow Z\)

联合概率分布:
\[p(x, y, z) = p(x) p(y|x) p(z|y)\]

条件概率:
\[p(x, z|y) = \frac{p(x, y, z)}{p(y)} = \frac{p(y)p(x|y)p(z|y)}{p(y)} = p(x|y)p(z|y)\]

因此，\(X \perp Z | Y\)。观察中间节点\(Y\)会将链断开（如同马尔可夫链）。

• \(X \leftarrow Y \rightarrow Z\)

联合概率分布:
\[p(x, y, z) = p(y) p(x|y) p(z|y)\]

条件概率:
\[p(x, z|y) = \frac{p(x, y, z)}{p(y)} = \frac{p(y)p(x|y)p(z|y)}{p(y)} = p(x|y)p(z|y)\]

因此，\(X \perp Z | Y\)。观察根节点\(Y\)将其子节点分开（如同朴素贝叶斯分类器）。

• \(X \rightarrow Y \leftarrow Z\)

联合概率分布:
\[p(x, y, z) = p(x) p(z) p(y|x, z)\]

条件概率:
\[p(y∣x,z)p(y)p(x, z|y) = \frac{p(x)p(z)p(y|x, z)}{p(y)}\]

此时，\(X \not\perp Z | Y\)。但我们注意到在无条件分布中：\(p(x, z) = p(x)p(z)\)说明\(X\)和\(Z\)是边际独立的。然而，观察到一个共同子节点\(Y\)使得其父节点\(X\)和\(Z\)变得相关，这种现象被称为 Explaining Away或 Berkson's paradox。

4.2 Berkson's paradox的例子

书中给了几个例子来直观展示Berkson's paradox：

示例 1：掷硬币实验

• 假设我们掷两个硬币100次，并且只记录至少有一个硬币是正面朝上的结果。这意味着我们会忽略双反的情况。
• 在这种情况下，每当硬币1为反面时，硬币2必定为正面，这导致了一个假象，即硬币1和硬币2似乎相关。
• 但实际上，这种相关性是由于选择偏差引起的，即我们只记录特定条件下的数据，从而扭曲了它们的实际独立性。

示例 2：高斯分布图模型 (DPGM)

• 我们有一个\(X \rightarrow Z \leftarrow Y\)的图结构，且联合分布为：\(p(x, y, z) = N(x | -5, 1) N(y | 5, 1) N(z | x + y, 1)\)
• 当我们不对\(Z\)进行条件化时，\(X\)和\(Y\)是独立的。然而，如果我们只选择\(z > 2.5\)的样本，会发现\(X\)和\(Y\)变得相关，这也是由于选择偏差导致的。

4.3 Markov Blankets

Markov Blankets是指，使某个节点与图中其他所有节点条件独立的最小节点集。对于一个节点\(i\)，它的马尔可夫包络\(mb(i)\)包括它的父节点、子节点和共同父节点（与其子节点有共同父母的节点），形式化表示为：

\[mb(i) ≜ ch(i) ∪ pa(i) ∪ copa(i)\]

其中\(ch(i)\)表示节点\(i\)的子节点，\(pa(i)\)是它的父节点，\(copa(i)\)是它子节点的共同父节点。

我们通过分解节点的联合分布，证明节点\(i\)的条件概率\(p(X_i | X_{-i})\)仅取决于马尔可夫包络中的节点。最终条件概率为：

\[p(x_i | x_{-i}) = p(x_i | x_{mb(i)}) \propto p(x_i | x_{mb(i)}) \prod_{Y_j \in ch(i)} p(x_k | x_{pa(k)})\]

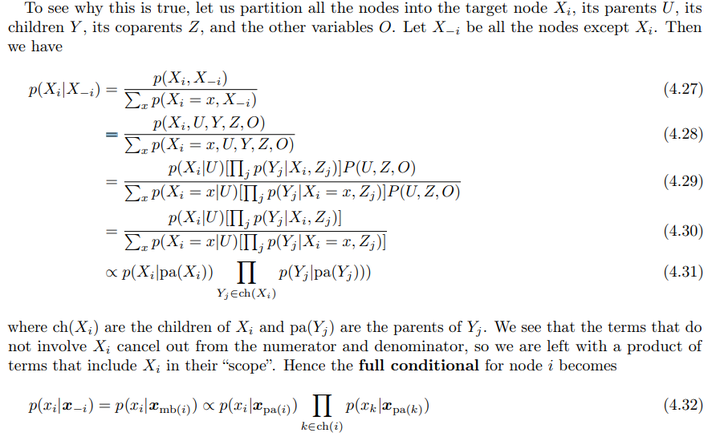
4.4 其他马尔可夫性质

通过d-分离准则，可以得出局部马尔可夫性质：

\[i \perp nd(i) \setminus pa(i) | pa(i)\]

其中\(nd(i)\)表示节点\(i\)的非后代节点，即除了它的后代以外的其他节点。局部马尔可夫性质表示，一个节点在已知它的父节点的条件下，与它的非后代独立。

同时，考虑上面结论的一个特殊情况，就可以得到有序马尔可夫性质：

\[i \perp pred(i) \setminus pa(i) | pa(i)\]

其中\(pred(i)\)是节点\(i\)的前驱节点（根据某个拓扑排序）。这些性质与全局马尔可夫性质 、局部马尔可夫性质 、有序马尔可夫性质之间有递推关系，最终这些性质是等价的。

5. 采样（Sampling）和推理（Inference）

从一个有向概率图模型中生成样本是简单的。我们可以按照拓扑顺序访问节点，即先访问父节点再访问子节点，然后根据父节点的值为每个节点采样。这个过程称为祖先采样（ancestral sampling），它能够生成来自联合分布的独立样本。

在PGMs中，推理指的是在已知一组可观察节点\(V\)的情况下，计算一组查询节点\(Q\)的后验分布，同时对不相关的干扰变量\(R\)进行边际化：

\[p_\theta(Q | V) = \frac{p_\theta(Q, V)}{p_\theta(V)} = \frac{\sum_{R} p_\theta(Q, V,R)}{p_\theta(V)}\]

如果\(Q\)是单个节点，则\(p_\theta(Q | V)\)被称为节点\(Q\)的后验边际。

例子：

设\(V = x\)为观察到的声音波形序列，\(Q = z\)为未知的说话单词，\(R = r\)为与信号相关的其它因素（如音调或背景噪声）。我们的目标是计算在给定声音的情况下，单词的后验分布：
\[p_\theta(z | x) = \sum_r p_\theta(z, r | x) = \sum_{r}{\frac{p_{\theta}(z,r,x)}{\sum_{r',z'}{p_{\theta}}(z',r',x)}}\]

为了简化，我们可以将随机因子\(R\)与查询集合\(Q\)合并，定义隐藏变量的完整集合\(H = Q \cup R\)：
\[p_\theta(h | x) = \frac{p_\theta(h, x)}{p_\theta(x)} = \frac{p_\theta(h, x)}{\sum_{h'} p_\theta(x, h')}\]

计算复杂度：推理任务的计算复杂度依赖于图的条件独立性属性，通常是NP-hard的，但对于某些图结构（如链、树和稀疏图），可以有效地用动态规划方法解决。

6. 学习

学习的目标是从数据中计算后验分布\(p(\theta | D)\)。在机器学习中，通常计算参数的点估计，例如最大化后验：\(\hat{\theta} = \arg\max p(\theta | D)\)

6.1 从完整数据中学习

下面给出一个具体的图模型进行示范：

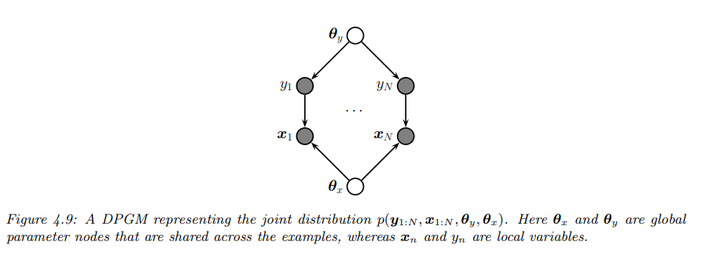
图示描述了一个典型的监督学习问题，其中有\(N\)个局部变量\(x_n\)和\(y_n\)，以及两个全局变量，代表数据样本共享的参数。局部变量为观察到的（训练集中），以实心（阴影）节点表示；全局变量为未观察到的，以空心（无阴影）节点表示。

根据图的条件独立性属性，联合分布因式分解为每个节点的乘积：
\[\begin{align*} p(\theta, D) &= p(\theta_x) p(\theta_y) \prod_{n=1}^{N} p(y_n | \theta_y) p(x_n | y_n, \theta_x) \\ &= \left( p(\theta_y) \prod_{n=1}^{N} p(y_n | \theta_y) \right) \left( p(\theta_x) \prod_{n=1}^{N} p(x_n | y_n, \theta_x) \right) \\ &= [p(\theta_y) p(D_y | \theta_y)] [p(\theta_x) p(D_x | \theta_x)] \end{align*}\]

其中\(D_y = \{y_n\}_{n=1}^{N}\)​ 和\(D_x = \{x_n, y_n\}_{n=1}^{N}\)分别为足以估计\(\theta_y\)和\(\theta_x\)​ 的数据。

我们可以独立地计算每个参数的后验分布：
\[p(\theta, D) = \prod_{i=1}^{N_G} p(\theta_i)p(D_i | \theta_i)\]

从而得出最大似然估计：
\[\hat{\theta} = \arg\max_{\theta} \prod_{i=1}^{N_G} p(D_i | \theta_i)\]

6.2 不完整数据中学习(隐变量)

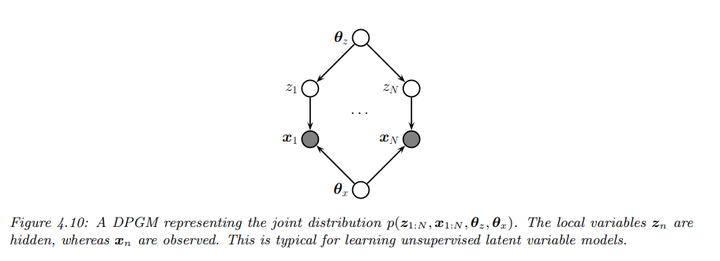
如上图，当存在隐变量时，似然函数的因式分解不再适用，因此无法独立地估计CPD。对于观测数据的似然性，可以写成：

\[\begin{align*} p(D | \theta) &= \sum_{z_{1:N}} \prod_{n=1}^{N} p(z_n | \theta_z) p(x_n | z_n, \theta_x) \\ &= \prod_{n=1}^{N} \sum_{z_{n}} p(z_n | \theta_z) p(x_n | z_n, \theta_x) \end{align*}\]

对数函数无法在求和上进行分解：

\[\ell(\theta) = \sum_{n} \log \sum_{z_n} p(z_n | \theta_z) p(x_n | z_n, \theta_x)\]

所以就有了如下的两种方法：

• 使用EM算法

期望步骤（E步）：在这个步骤中，算法推断隐变量\(z_n\)​ 的期望值，而不是返回其完整的后验分布\(p(z_n | x_n, \theta^{(t)})\)。这样做是为了降低计算复杂性，返回期望充分统计量（ESS），即隐变量的加权计数。

最大化步骤（M步）：在这个步骤中，使用E步中计算的ESS来最大化完全观察数据的对数似然期望值。这意味着在这个步骤中，参数更新基于对隐变量的期望。

• 使用SGD拟合

EM是批处理算法，使用随机梯度下降（SGD）更适合大规模数据集。我们需要为每个示例计算观测数据的边际似然：
\[p(x_n | \theta) = \sum_{z_n} p(z_n | \theta_z) p(x_n | z_n, \theta_x)\]

对数似然计算：
\[l(\theta) = \log p(D | \theta) = \sum_{n=1}^{N} \log p(x_n | \theta)\]

梯度计算：

\[\begin{align*} \nabla_\theta \ell(\theta) &= \sum_n \nabla_\theta \log p(x_n|\theta) \\ &= \sum_n \frac{1}{p(x_n|\theta)} \nabla_\theta p(x_n|\theta) \\ &= \sum_n \frac{1}{p(x_n|\theta)} \nabla_\theta \left( \sum_{z_n} p(z_n, x_n|\theta) \right) \\ &= \sum_n \sum_{z_n} \frac{p(z_n, x_n|\theta)}{p(x_n|\theta)} \nabla_\theta \log p(z_n, x_n|\theta) \\ &= \sum_n \sum_{z_n} p(z_n|x_n, \theta) \nabla_\theta \log p(z_n, x_n|\theta) \end{align*}\]

当然，这种几种做法需要我们知道隐变量的后验分布，但在深度学习中，很多时候是不知道的。这时候比如VAEs就是直接优化最大似然下界，相当于只进行了EM算法中的M步。

二、无向图模型（马尔可夫随机场）

在某些领域，比如图像，去定义像素之间的联系的方向是不自然的。我们可以说一个像素与周围像素有关，但为这种关系定义一个方向（即建模一个有向图模型），其实并不是自然或者合理的。此时用无向图模型，不指定边的方向，更自然地处理这些问题。相比有向图模型，无向图模型（UPGM）具有对称性，特别适用于空间或关系数据。

1. 联合分布

在无向图中，由于没有拓扑顺序，无法使用链规则来表示联合分布\(p(x_1, \ldots, x_N)\)。相反，联合分布通过图中的最大团（maximal cliques）来表示。每个最大团关联一个势函数，记为\(\psi_c(x_c; \theta_c)\)，其中\(x_c\)​ 是该团的变量，\(\theta_c\)​ 是其参数。这些势函数可以是任何非负函数。

团是一个无向图中的完全子图，其中任意两个节点都相互连接。在一个图中，最大团是不能再扩展的团，即如果再添加任何一个节点，这个团将不再是完全连接的。

• Hammersley-Clifford定理

如果联合分布\(p\)满足由无向图\(G\)所隐含的条件独立性（CI）属性，那么可以写成以下形式： \[p(x|\theta) = \frac{1}{Z(\theta)} \prod_{c \in C} \psi_c(x_c; \theta_c)\]

其中\(C\)是图\(G\)的所有最大团的集合，\(Z(\theta)\)是归一化因子（partition function），确保整体分布的总和为1： \[Z(\theta) = \sum_x \prod_{c \in C} \psi_c(x_c; \theta_c)\]

• Gibbs分布

Hammersley-Clifford定理中的分布可以重写为：

\[p(x|\theta) = \frac{1}{Z(\theta)} \exp(-E(x; \theta))\]

其中\(E(x; \theta)\)是状态\(x\)的能量，定义为所有团的能量之和： \[E(x; \theta) = \sum_c E(x_c; \theta_c)\]

势函数可以通过能量定义为：

\[\psi_c(x_c; \theta_c) = \exp(-E(x_c; \theta_c))\]

这表明低能量状态与高概率状态相关联。Gibbs分布也称为基于能量的模型，广泛用于物理和生物化学领域，同时也在机器学习中用于定义生成模型。此外，条件随机场（CRFs）是一种特定形式的能量基础模型，形式为\(p(y|x, \theta)\)，其中势函数基于输入特征\(x\)。

2. 全可见的马尔可夫随机场（Fully visible MRFs）

Fully visible MRFs指的是无向图模型中不存在潜变量，即除了参数以外，所有的节点都是数据的一部分。

书中给了几个例子，这里只记录Ising models一个例子

Ising模型是一种特定的马尔可夫随机场（MRF），用于表示二元变量的联合分布。在一个二维格子（lattice）中，节点表示原子，每个原子可以有两个状态（+1或-1），这通常用于表示磁性材料中的自旋。其对应的无向图如下：

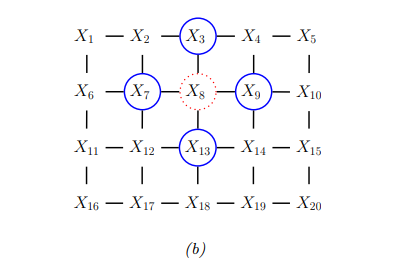
联合分布可以表示为： \[p(x|\theta) = \frac{1}{Z(\theta)} \prod_{i \sim j} \psi_{ij}(x_i, x_j; \theta)\] 其中\(i \sim j\)表示节点\(i\)和\(j\)是邻居。

• 势函数：对于Ising模型，势函数定义为： \[\psi_{ij}(x_i, x_j; \theta) = \begin{cases} e^{J_{ij}} & \text{如果 } x_i = x_j \\ e^{-J_{ij}} & \text{如果 } x_i \neq x_j \end{cases}\]

\(J_{ij}\)​ 是节点之间的耦合强度。若两个节点不相连，则\(J_{ij} = 0\)。

• 能量模型：Ising模型通常以能量为基础定义： \[p(x|\theta) = \frac{1}{Z(J)} \exp(-E(x; J))\] 能量函数为： \[E(x; J) = -J \sum_{i \sim j} x_i x_j\]

其中，\(x_i x_j\)的值为：

\[+1（当 x_i = x_j​ 时）\\ −1（当 x_i \neq x_j 时）\]

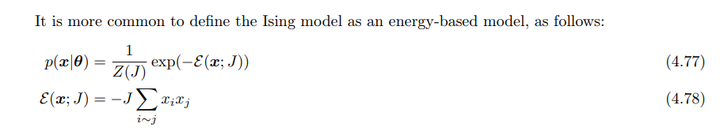
• 耦合强度与温度：耦合强度\(J\)控制邻近节点之间的相互作用程度。可以通过引入温度\(T\)来调整\(J\)，设\(J' = J/T\)，这意味着：温度较低时（冷），节点之间的耦合较强（\(J\)较大）。温度较高时（热），节点之间的耦合较弱（\(J\)较小）。
• 磁性系统的特性：如果所有权重为负（\(J < 0\)），节点倾向于与邻居不同，形成反铁磁系统，导致系统受挫，因为在二维格子中不可能所有邻居都不同；如果所有边的权重为正（\(J > 0\)），邻近节点更可能处于相同状态，这被称为铁磁模型。

• 引入外场：除了成对项（pairwise terms），通常还会加入单项（unary terms），称为外部场。模型可以表示为： \[p(x|\theta) = \frac{1}{Z(\theta)} \prod_i \psi_i(x_i; \theta) \prod_{i \sim j} \psi_{ij}(x_i, x_j; \theta)\]

对于每个节点，外部势函数定义为： \[\psi_i(x_i) = \begin{cases} e^{\alpha} & \text{如果 } x_i = +1 \\ e^{-\alpha} & \text{如果 } x_i = -1 \end{cases}\]

其能量模型为： \[E(x|\theta) = -\alpha \sum_i x_i - J \sum_{i \sim j} x_i x_j\]

3. MRFs与潜在变量

对于包含潜变量的MRFs，书中举了著名的Boltzmann机作为例子。

• 普通Boltzmann机器允许任意的图结构，但确切的推理和学习在普通Boltzmann机器中是不可行的，近似推理（如Gibbs抽样）通常很慢。
• 限制Boltzmann机器（RBMs）将节点分为两层，且同层节点之间没有连接。这种结构使得推理更加高效，因为隐藏节点在给定可见节点的条件下是独立的。RBMs通常具有二元节点，能量项形式为\(w_{dk} x_d z_k\)，其中\(z_k\)决定隐藏单元的活跃状态。
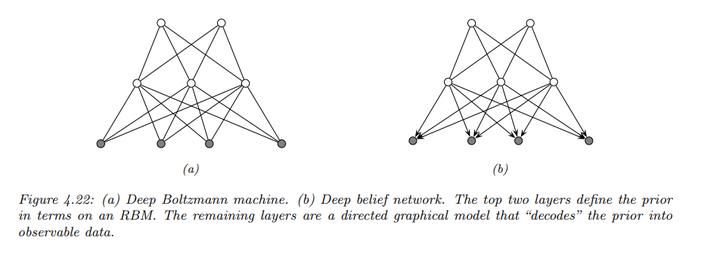
• 深度Boltzmann机器通过堆叠多个RBM层来构建深度Boltzmann机器，进一步提高模型的表示能力。
• 深度belief网络（DBNs）结合了RBM和生成模型（DPGM），作为潜在分布编码的先验，并将其转换为观察数据。DBN可以以贪婪方式进行训练，支持快速的自下而上的推理。

4. 最大熵模型

最大熵模型的目标是在特征符合经验期望的条件下，构建具有最大熵的分布。其形式为： \[p(x|\theta) = \frac{1}{Z(\theta)} \exp(\theta^T \phi(x))\]

在前面我们也提到，指数族分布是满足最大熵的分布。

在某些应用中，特征\(\phi(x)\)可以预先定义，但也可以通过无监督学习进行诱导。这种特征诱导（Feature induction）的方法通常从基础特征开始，逐步生成新的特征组合（书中也没有细讲）。

总归最大熵模型也算是很经典也很熟悉的一个模型了。

5. 条件独立性

在给定三个节点集\(A\)、\(B\)和\(C\)的情况下，如果在图\(G\)中，去掉所有\(C\)中的节点后，\(A\)中的任一节点与\(B\)中的任一节点之间没有路径相连，则称\(X_A\)​ 在\(X_C\)​ 条件下与\(X_B\)​ 条件独立。用符号表示为：

\[X_A \perp_G X_B | X_C\]

这也被称为UPGMs的全局马尔可夫性质。例如，在下面的图中，{X1, X2} 条件独立于 {X6, X7} 给定 {X3, X4, X5}。

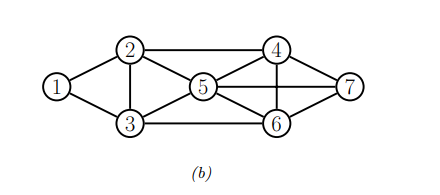
使节点\(t\)条件独立于图中其他所有节点的最小节点集称为\(t\)的马尔可夫毯（Markov blanket），记作\(mb(t)\)。也就是说： \[t \perp V \setminus cl(t) | mb(t)$，其中$cl(t) \equiv mb(t) \cup \{t\}\] \(V\)是图中所有节点的集合。

可以证明，在UPGM中，节点的马尔可夫毯正是其直接邻居。这被称为无向局部马尔可夫性质（undirected local Markov property）。例如，上图中对于节点 X5，其马尔可夫毯为 {X2, X3, X4, X6, X7}。

根据局部马尔可夫性质，可以得出，如果两个节点之间没有直接边，则它们在其余节点条件下是条件独立的。这称为成对马尔可夫性质（pairwise Markov property）：

\[s \perp t | V \setminus \{s, t\} \iff G_{st} = 0\]

其中\(G_{st} = 0\)表示\(s\)和\(t\)之间没有边。

全局马尔可夫性质蕴含局部马尔可夫性质，局部马尔可夫性质又蕴含成对马尔可夫性质。相对不明显的是，成对马尔可夫性质可以推导出全局马尔可夫性质，因此这些马尔可夫性质实际上是相同的。

6. 采样（sampling）与推断（Inference）

与有向概率图模型相比，从UPGM中采样（sampling）可能会比较慢，因为UPGM中的变量没有顺序。此外，除非知道归一化常数\(Z\)的值，否则很难计算任何配置的概率。

由于这些挑战，通常使用马尔可夫链蒙特卡洛（MCMC）方法来从UPGM中生成样本。MCMC方法通过构建一个状态空间并在该空间中进行随机游走，逐步收敛到目标分布。

对于特殊的的UPGM，也可以使用结点树算法（junction tree algorithm）通过动态规划生成样本。

至于Inference，书中仅给了一个去噪的例子，具体内容会在第九章进行讲述。

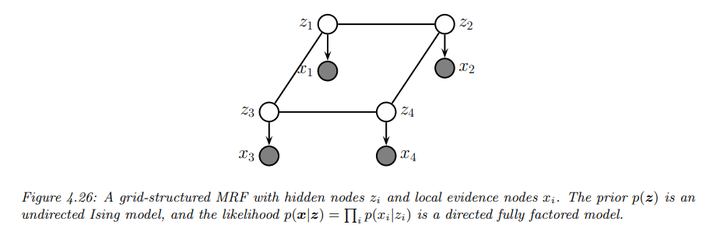
• 模型描述：假设我们有一个由二进制像素\(z_i\)​ 组成的图像，但我们只观察到像素的噪声版本\(x_i\)​。该联合模型的形式为：
  \[p(x,z)=p(z)p(x|z) = \left[ \frac{1}{Z} \prod_{i \sim j} \psi_{ij}(z_i, z_j) \right] \prod_{i} p(x_i | z_i)\]

其中\(p(z)\)是一个Ising model先验，而\(p(x_i | z_i) = N(x_i | z_i, \sigma^2)\)，\(z_i\)取值为 {-1, +1}。

• 链图（Chain Graph）：这个模型在先验上使用UPGM，而在似然部分使用有向边，形成一种称为链图的混合模型。

• 后验推断：推断任务是计算后验边际\(p(z_i | x)\)，以及后验最大后验估计（MAP）：\(\text{argmax}_z \, p(z | x)\)

由于对于大网格的精确计算是不可行的，因此必须使用近似方法。可以使用多种算法进行推断，包括均值场变分推断（mean field variational inference）、吉布斯采样（Gibbs sampling）、循环信念传播（loopy belief propagation）等。

7. 学习

即使在完全观测的情况下，计算最大似然估计（MLE）也可能非常耗费计算资源，因为需要处理归一化常数\(Z(\theta)\)。而计算参数的后验分布\(p(\theta | D)\)则更加困难，因为还需要额外的归一化常数\(p(D)\)，这被称为双重不可解问题（doubly intractable）。

7.1 从完全观测数据中学习

完全观测数据指的是训练过程中没有隐藏变量或缺失数据（即完全观测数据设置）。此时MRF的分布形式为：

\[p(x|\theta) = \frac{1}{Z(\theta)} \exp\left( \sum_{c} \theta^T_c \phi_c(x) \right)\]

其中，\(c\)表示团，\(Z(\theta)\)是归一化常数，\(\theta_c\)​ 是参数向量，\(\phi_c(x)\)是对应的特征函数。

则对数似然可以表示为：

\[\ell(\theta) \triangleq \frac{1}{N} \sum_{n} \log p(x_n | \theta) = \frac{1}{N} \sum_{n} \left[ \sum_{c} \theta_c^T \phi_c(x_n) - \log Z(\theta) \right]\]

在指数族中，我们已经知道了

\[\frac{\partial \log Z(\theta)}{\partial \theta_c} = \mathbb{E}[\phi_c(x) | \theta] = \sum_{x} p(x | \theta) \phi_c(x)\]

所以其梯度为：

\[\frac{\partial \ell}{\partial \theta_c} = \frac{1}{N} \sum_{n} \left[ \phi_c(x_n) - \mathbb{E}[\phi_c(x)|\theta] \right]\]

其中，\(\mathbb{E}[\phi_c(x)|\theta]\)表示在模型下特征函数的期望值。当数据的期望值与模型的期望值相等时，梯度为零，这被称为矩匹配（moment matching）。评估来自数据的期望值，称为正相（positive phase），因为\(x\)被固定为观测值。评估来自模型的期望值，称为负相（negative phase），因为\(x\)在模型中可以自由变化。

在特定情况下，可以使用迭代比例拟合算法（iterative proportional fitting, IPF）进行迭代优化。然而，在一般情况下，通常使用梯度下降方法进行参数估计。

7.2 计算的细节问题

计算MRF和条件随机场（CRF）时，MLE的最大计算瓶颈是计算对数归一化常数\(Z(\theta)\)的导数：

\[\frac{\partial \log Z(\theta)}{\partial \theta} = \mathbb{E}_{p(x|\theta)}[\nabla_\theta \log \tilde{p}(x|\theta)]\]

由于需要在每一步梯度下降训练时从模型中采样，计算梯度变得非常耗时。所以除了MLE，还可以使用其他估计方法：对比散度（contrastive divergence）和伪似然估计（pseudolikelihood estimation）。这两个是生成模型里面比较常见的方法。

7.3最大伪似然估计（Maximum Pseudolikelihood Estimation, MPLE）

伪似然是一种替代MLE的简单方法，定义如下：

\[\ell_{PL}(\theta) = \frac{1}{N} \sum_{n=1}^{N} \sum_{d=1}^{D} \log p(x_{nd}|x_{n,-d}, \theta)\]

伪似然优化的是全条件概率的乘积，也称为复合似然（composite likelihood）。这里\(x_{n,-d}\)表示除了\(x_d\)​ 外的其他变量。\(x_{nd}\)通常表示第\(n\)个样本的第\(d\)个变量或特征

MPLE在某些情况下是MLE的近似，但通常不是最优的（在某些特殊模型如高斯MRF中，MPLE与MLE等价）

与MLE相比，伪似然更快，因为计算每个节点的全条件概率只需对单个节点的状态求和，而不需要计算全局归一化常数。同时，尽管伪似然在一般情况下不等同于MLE，但它在大样本极限下是一致估计量。一些具体实践中的表现如下：

7.4 从不完全观测数据中学习

在一些应用中，我们可能只观察到部分数据，其他数据（隐藏变量）是不可见的。例如，我们可能希望从噪声图像\(x\)中推断出一个“干净”的图像\(z\)。这样的模型被称为隐 Gibbs 随机场。

模型的联合分布形式为：

\[p(x, z | \theta) = \frac{\exp(\theta^T \phi(x, z))}{Z(\theta)}\]

对数似然\(\ell(\theta)\)的表达式为：

\[\begin{align*} \ell(\theta) &= \frac{1}{N} \sum_{n=1}^{N} \log \left( \sum_{z_n} p(x_n, z_n | \theta) \right) \\ &= \frac{1}{N} \sum_{n=1}^{N} \log \left( \frac{1}{Z(\theta)} \sum_{z_n} \tilde{p}(x_n, z_n | \theta) \right) \\ &= \frac{1}{N} \sum_{n=1}^{N} \left( \log \sum_{z_n} \tilde{p}(x_n, z_n | \theta) - \log Z(\theta) \right) \end{align*}\]

我们可以把第一项写成如下形式：

\[\begin{align*} \log \sum_{z_n} \tilde{p}(x_n, z_n | \theta) &= \log \sum_{z_n} \exp(\theta^T \phi(x_n, z_n)) \\ &\triangleq \log Z(\theta, x_n) \end{align*}\]

这表示在给定\(x_n\)​ 的情况下，隐藏变量\(z\)的所有可能值的对数分区函数。

这样对数似然的梯度可以表示为：

\[\frac{\partial \ell}{\partial \theta} = \frac{1}{N} \sum_{n} \left( E_{z \sim p(z | x_n, \theta)}[\phi(x_n, z)] - E_{(z,x) \sim p(z,x | \theta)}[\phi(x, z)] \right)\]

这个表达式的意思是，梯度是由两个期望值的差组成的：

• 第一个期望值是条件在观测到的\(x_n\)下，对应于隐藏变量\(z\)的期望。
• 第二个期望值是在无条件情况下对\(z\)和\(x\)的期望。

三、 条件随机场（CRFs）

CRF 是一种建模条件分布的马尔科夫随机场的模型，它通过输入节点\(x\)预测输出节点\(y\)的联合概率。其模型形式为：

\[p(y|x, \theta) = \frac{1}{Z(x, \theta)} \prod_{c} \psi_c(y_c; x, \theta)\]

这里的分区函数\(Z(x, \theta)\)不仅依赖于参数\(\theta\)，还依赖于输入\(x\)，反映了输入对模型输出的影响。

势函数\(\psi_c(y_c; x, \theta)\)可以采用对数线性形式：\(\psi_c(y_c; x, \theta) = \exp(\theta^T_c \phi_c(x, y_c))\)，CRF 可以使用非线性势函数（如深度神经网络）来增强建模能力。

CRF 能够捕捉输出标签之间的依赖关系，适用于结构化预测问题，例如序列标签或图节点的标签。它允许对输出的有效值施加约束，如在句法分析中，必须遵循语法规则。

1. 一维的CRFs

1D CRFs 是基于链式结构的图模型，用于定义给定输入序列\(x_{1:T}\)下的输出序列\(y_{1:T}\)​ 的联合概率分布。公式如下：

\[\begin{equation} p(y_{1:T} | x, \theta) = \frac{1}{Z(x, \theta)} \prod_{t=1}^{T} \psi(y_t, x_t; \theta) \prod_{t=2}^{T} \psi(y_{t-1}, y_t; \theta) \end{equation}\]

其中\(ψ(y_t, x_t; θ)\)是节点势，\(ψ(y_{t-1}, y_t; θ)\)是边势。

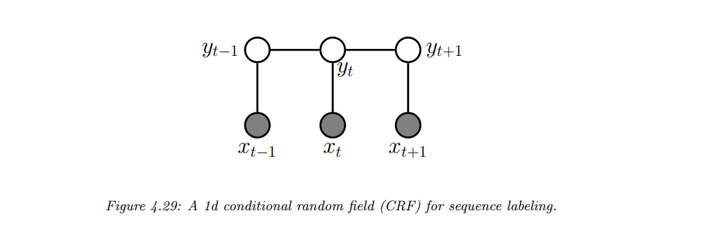
值得注意的是有一种模型可以看成这类任务的另一种建模方法，即最大熵马尔可夫模型（MEMM）：

\[\begin{equation} p(y_{1:T} | x, \theta) = p(y_1 | x_1; \theta) \prod_{t=2}^{T} p(y_t | y_{t-1}, x_t; \theta) \end{equation}\]

在最大熵马尔可夫模型中，条件概率\(p(y_t|y_{t-1}, x_t; θ)\)是局部归一化的。这意味着每个条件的计算仅依赖于前一个标签和当前输入，而不能有效地利用全局上下文信息，这在某些情况下可能导致模型性能的下降。具体模型可以看成一个DPGM：

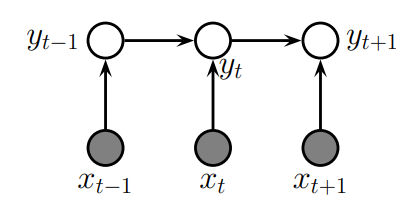
具体应用示例：

CRFs 在1980年代到2010年代的自然语言处理（NLP）领域得到了广泛应用，尤其是在序列标注任务中。然而，随着深度学习的发展，RNN 和 Transformer 等模型逐渐取代了 CRFs。

• 名词短语分块（Noun Phrase Chunking）

任务描述：在信息提取中，将句子解析为名词短语和动词短语，并为每个单词分配词性标签。

使用 BIO（Beginning, Inside, Outside）标注方法来标识名词短语的起始、内部和外部。例如，序列 OBIIO 和 OBIOBIO 是有效的标注，表明它们分别代表一个名词短语和两个相邻的名词短语。

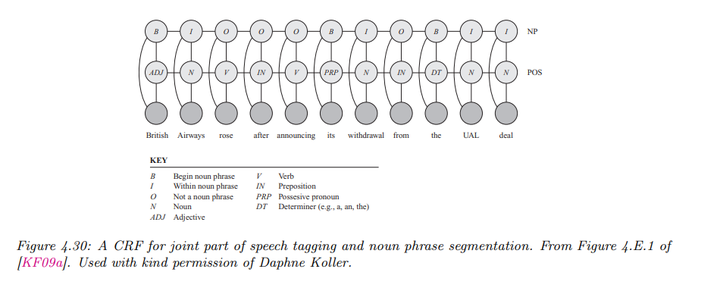
• 命名实体识别（Named Entity Recognition）

任务描述：不仅对名词短语进行标注，还将其分类为不同类型（如人名、地名、组织名等）。

BIO 扩展：采用扩展的 BIO 标签来处理不同类型的命名实体（B-Per, I-Per, B-Loc, I-Loc, B-Org, I-Org, Other）。

长距离依赖：通过考虑词之间的长距离相关性，提高模型性能。这种模型被称为跳链 CRF（skip-chain CRF）。

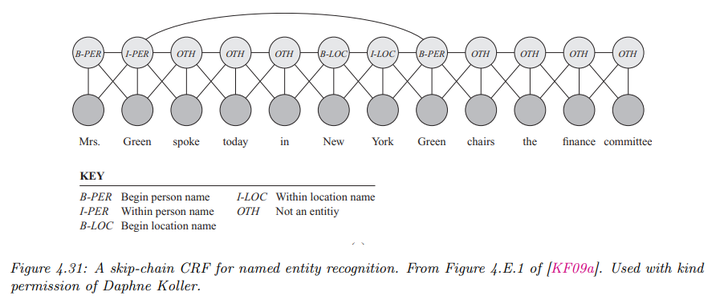
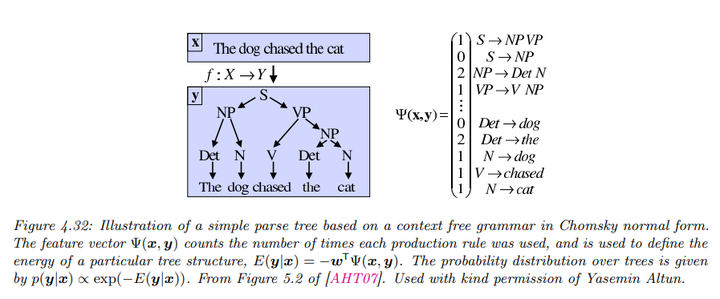
• 自然语言解析（Natural Language Parsing）

使用概率上下文无关文法（PCFG），PCFG 是一种生成模型，定义了一组重写或生成规则，形式为\(\sigma \rightarrow \sigma' \sigma''\)或\(\sigma \rightarrow x\)，其中\(\sigma, \sigma', \sigma''\)是非终结符（类似于词性），而\(x\)是终结符（即单词）。

每个规则都有一个相关的概率，从而定义了一个词序列的概率分布。但为了计算观察到特定序列\(x = x_1, \ldots, x_T\)​ 的概率，需要对所有生成该序列的树进行求和。这一过程可以通过算法在\(O(T^3)\)的时间复杂度内完成。

可以通过深度神经网络来定义特征，使得解析器能够更好地捕捉语言中的复杂模式。

2. 二维的CRFs

CRFs 还可以应用于图像处理问题，这些问题通常定义在二维网格上。模型的条件概率形式为：

\[p(y|x) = \frac{1}{Z(x)} \left[ \sum_{i \sim j} \psi_{ij}(y_i, y_j) \right] \prod_i p(y_i|x_i)\]

这里，\(\psi_{ij}(y_i, y_j)\)是节点之间的潜在函数。

具体应用示例：

• 语义分割

语义分割的任务是为图像中的每个像素分配标签。虽然可以使用卷积神经网络（CNN）解决此问题，但由于卷积是局部操作，可能无法捕获长程依赖。

所以将CNN的输出传入CRF，尤其是完全连接的CRF，可以更好地捕捉长距离连接。完全连接CRF的推理复杂度较高，但通过高斯势函数可以使用均值场算法进行有效推理。

\[p(y|x) = \frac{1}{Z(x)} \left[ \prod_i p(y_i|f(x)_i) \cdot \prod_{(i,j) \in E} \psi(y_i, y_j | x) \right]\]

这里，\(E\)是CRF中的边集，\(f(x)_i\)​ 是CNN的输出

• 目标检测

为给定类别（如人或车）找到图像中的对象位置。传统的滑动窗口检测器可能对形状可变的对象（如人的身体）表现不佳。

部件分解策略：将对象分解为部件，使用成对的CRF来确保部件之间的空间一致性。例如，使用势函数

\[\psi(y_i, y_j | x) = \exp(-d(y_i, y_j))\]

其中\(d(y_i, y_j)\)是\(i\)和\(j\)的距离函数，我们也可以设定让它与输入\(x\)相关，这样便可以鼓励相邻部件靠近。

最终模型形式类似：

\[p(y|x) = \frac{1}{Z(x)} \left[ \prod_i p(y_i|f(x)_i) \cdot \prod_{(i,j) \in E} \psi(y_i, y_j | x) \right]\]

3. 参数估计

对于参数的估计，我们仍然使用最大似然估计，我们假设势函数是线性的：

\[\psi_c(y_c; x, \theta) = \exp(\theta^T_c \phi_c(x, y_c) )\]

根据势函数的定义，似然函数为：

\[\log p(y_n | x_n, \theta) = \sum_c \theta^T_c \phi_c(y_{n,c}, x_n) - \log Z(x_n; \theta)\]

其中，分区函数\(Z(x_n; \theta)\)定义为：

\[Z(x_n; \theta) = \sum_y \exp(\theta^T \phi(y, x_n))\]

接下来，我们定义对数似然：

\[\begin{align*} \ell(\theta) &= \frac{1}{N} \sum_n \log p(y_n | x_n, \theta) \\ &= \frac{1}{N} \sum_n [\sum_c \theta^T_c \phi_c(y_{n,c}, x_n) - \log Z(x_n; \theta)] \end{align*}\]

根据链式法则，似然函数的导数为：

\[\frac{\partial \ell}{\partial \theta_c} = \frac{1}{N} \sum_n \left( \phi_c(y_{n,c}, x_n) - \frac{\partial}{\partial \theta_c} \log Z(x_n; \theta) \right)\]

由于\(\frac{\partial}{\partial \theta_c} \log Z(x_n; \theta)\)可以表示为期望值（前面证明过）：

\[\frac{\partial}{\partial \theta_c} \log Z(x_n; \theta) = \mathbb{E}_{p(y | x_n, \theta)}[\phi_c(y, x_n)]\]

因此，最终的梯度为：

\[\frac{\partial \ell}{\partial \theta_c} = \frac{1}{N} \sum_n \left( \phi_c(y_{n,c}, x_n) - \mathbb{E}_{p(y | x_n, \theta)}[\phi_c(y, x_n)] \right)\]

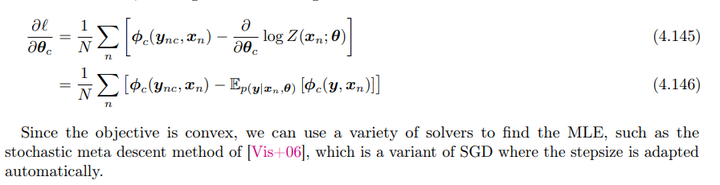
更一般情况下，CRF 可以写作：

\[p(y | x; \theta) = \frac{\exp(f(x, y; \theta))}{Z(x; \theta)}\]

其中\(f(x, y; \theta)\)是评分函数（负能量函数），高分对应于可能的情况。

对数似然的梯度为：

\[\nabla_\theta \ell(\theta) = \frac{1}{N} \sum_{n=1}^N \left( \nabla_\theta f(x_n, y_n; \theta) - \nabla_\theta \log Z(x_n; \theta) \right)\]

计算对数分区函数的导数是可行的，前提是我们能够计算对应的期望值。然而，需要注意的是，我们必须对每个训练样本计算这些导数，这比马尔可夫随机场（MRF）的情况要慢，因为MRF的对数分区函数是一个常数，独立于观测数据。

四、 有向图模型和无向图模型的比较

1. 表达能力

一个图\(G\)是分布\(p\)的 I-map 如果图中编码的所有条件独立（CI）关系都在分布中成立；完美图则能够精确表示分布的所有 CI 属性。

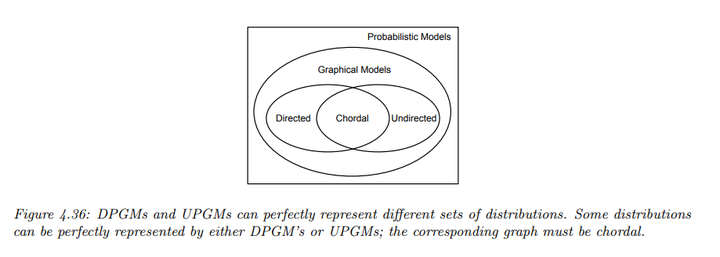
可以证明，DPGMs 和 UPGMs 能够建模不同的分布集，意味着两者在建模能力上并不优于对方。

• DPGM 的优越性：DPGM 可以精确表示 v-structure（如\(A \to C \leftarrow B\)），表明\(A\)与\(B\)独立，但在给定\(C\)时不独立。若将箭头去掉，得到的无向图会错误地表示其他独立关系。事实上，这种CI性质无向图模型建模不出来。
• UPGM 的优越性：如四循环的例子，UPGM 可以正确表示某些 CI 关系（例如\(A \perp C | B, D\)），而相应的 DPGM 无法精确编码所有关系。

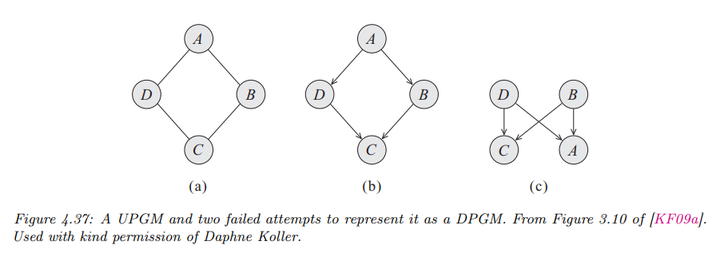
2. 有向图模型和无向图模型的转换

2.1 从有向图模型转化为无向图模型

在将有向概率图模型（DPGM）转换为无向概率图模型（UPGM）时，首先我们需要道德化（Moralization）。

即对于共享子节点的“未婚”父节点（即没有边连接的父节点），需要添加边以连接它们。这一步确保条件独立性（CI）属性在转换后依然保持一致。

一旦道德化完成，移除所有的箭头，得到一个无向图。

以学生网络为例：

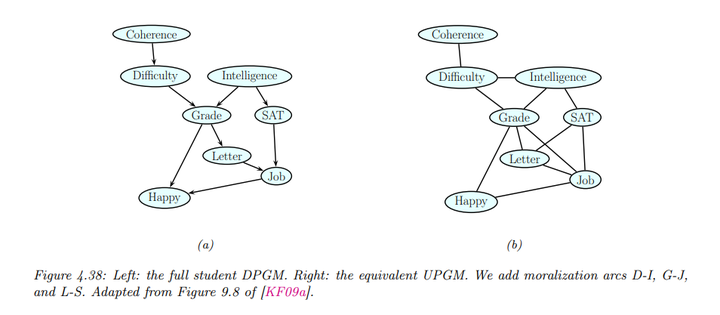
其联合分布如下：

\[P(C, D, I, G, S, L, J, H) = P(C)P(D|C)P(I)P(G|I, D)P(S|I)P(L|G)P(J|L, S)P(H|G, J)\]

接下来，为每个条件概率分布（CPD）定义势函数，得到：

\[p(C, D, I, G, S, L, J, H) = \psi_C(C) \psi_D(D, C) \psi_I(I) \psi_G(G, I, D) \psi_S(S, I) \psi_L(L, G) \psi_J(J, L, S) \psi_H(H, G, J)\]

所有的潜在函数都是局部归一化的，因为它们都是 CPD，因此归一化常数\(Z = 1\)

转换后的无向图如上所示，我们看到已经添加了以下的边：D-I，G-J，L-S，这些边连接了共享子节点的父节点，确保了在无向图中能够存储每个家庭的条件概率分布。

但需要注意的是转换过程中，某些条件独立性（CI）关系可能会被放宽或忽略，这样只是可以保证转换后的图能够表示原有图的一部分信息。

2.2 从无向图模型转化为有向图模型

将无向概率图模型（UPGM）转换为有向概率图模型（DPGM），我们首先需要创建虚拟节点：对于每个潜在函数\(\psi_c(x_c; \theta_c)\)，我们引入一个“虚拟节点”\(Y_c\)​，并将设置一个状态\(y^*_c\)​。

接着，我们定义条件概率分布\(p(Y_c = y^*_c | x_c) = \psi_c(x_c; \theta_c)\)。这表示在给定特征\(x_c\)的条件下，虚拟节点\(Y_c\)​ 取特定值的概率，与原UPGM中的潜在函数相对应。这样转换后的整体联合分布形式为\(p_{\text{undir}}(x) \propto p_{\text{dir}}(x, y^*)\)

具体示例：

考虑一个UPGM，其中联合分布为：
\[p(A, B, C, D) = \frac{\psi(A, B, C, D)}{Z}\]

为了转换成DPGM，我们添加一个虚拟节点\(E\)，使其成为所有其他节点的子节点，并设置\(E = 1\)。然后定义 CPD 为：
\[p(E = 1 | A, B, C, D) \propto \psi(A, B, C, D)\]

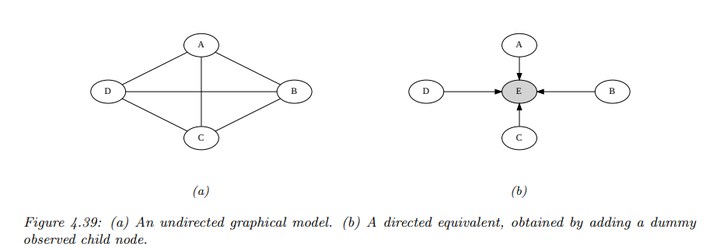
同样，这个过程中某些条件独立性（CI）关系可能会被放宽或忽略。

3. 有向图模型和无向图模型的结合

链图（Chain graphs）是一种可能包含有向和无向边的概率图模型，但不允许有向循环。它能够有效地结合两种类型的边，从而捕捉更复杂的依赖关系。

例如下图给出了一个简单的联合模型示例

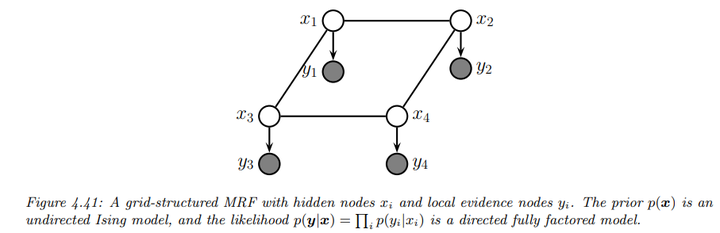
\[p(y_{1:D}|x_{1:D}) = \left[ \frac{1}{Z} \prod_{i \sim j} \psi_{ij}(x_i, x_j) \right] \prod_{i=1}^{D} p(y_i | x_i)\]

其中，\(p(x)\)由无向概率图模型（UPGM）定义，而\(p(y|x)\)则由有向概率图模型（DPGM）指定。

再比如如下的离散时间的二阶马尔科夫链：假设观测值是连续的\(x_t \in \mathbb{R}^D\)，其转移函数可以表示为线性高斯条件概率分布（CPD）：

\[p(x_t | x_{t-1}, x_{t-2}, \theta) = \mathcal{N}(x_t | A_1 x_{t-1} + A_2 x_{t-2}, Σ)\]

这种模型也被称为向量自回归模型（VAR process of order 2），广泛应用于时间序列预测和经济计量学中。

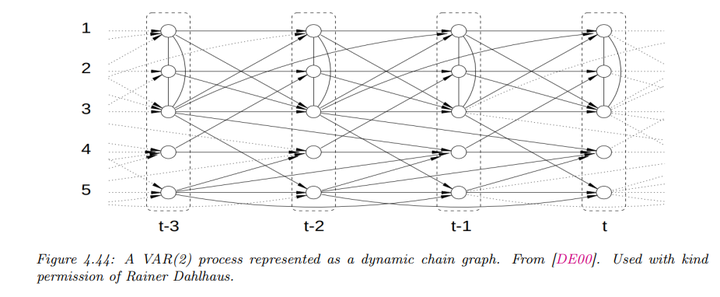
链图可以通过部分有向无环图（PDAG）来描述，PDAG可分解为一个有向图，其链组件的节点之间仅通过无向边连接。这允许对不同的条件概率分布进行更灵活的建模。例如下图：

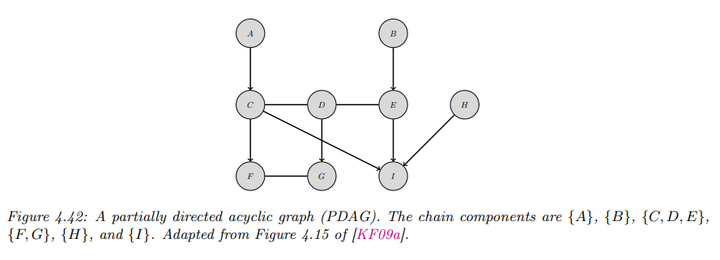
\[p(A, B, \ldots, I) = p(A) p(B) p(C, D, E | A, B) p(F, G | C, D) p(H) p(I | C, E, H)\]

这里的每个条件概率分布（CPD）对应于条件随机场（CRF），例如：

\[p(C, D, E | A, B) = \frac{1}{Z(A, B)} \phi(A, C) \phi(B, E) \phi(C, D) \phi(D, E)\] \[p(F, G | C, D) = \frac{1}{Z(C, D)} \phi(F, C) \phi(G, D) \phi(F, G)\]

五、 扩展概率图模型（PGM）

1. 因子图（Factor Graphs）

因子图（Factor Graphs）是一种扩展了的概率图模型（PGM），它将变量之间的依赖关系明确表示了出来。主要有两种形式的因子图：双部因子图（Bipartite Factor Graph）和Forney因子图（Forney Factor Graph, FFG）。

1.1 双部因子图（Bipartite Factor Graphs）

双部因子图是一种无向图，具有两种不同类型的节点：

• 圆形节点代表随机变量。
• 方形节点代表因子，因子对应于某些函数或潜在分布。

例子解释

考虑一个马尔可夫随机场（MRF），如下图所示：

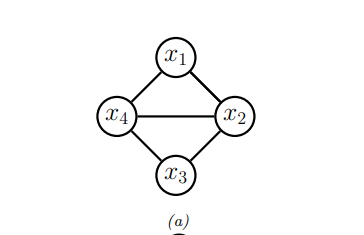
我们可以将每个最大团中的势函数转换为一个因子图。如下所示：

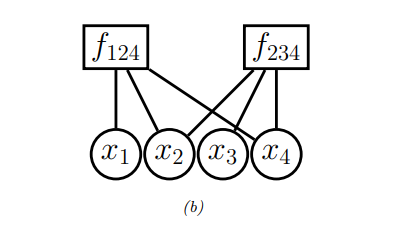
其中涉及变量\(x_1, x_2, x_3, x_4\)​，其联合分布表示为：

\[f(x_1, x_2, x_3, x_4) = f_{124}(x_1, x_2, x_4) f_{234}(x_2, x_3, x_4)\]

这里，每个因子代表一个这些变量的势函数。通过这种方式，因子图更直观详细地描述了变量间的关系。

我们还可以对每条边而不是每个团关联一个势函数，如下所示：

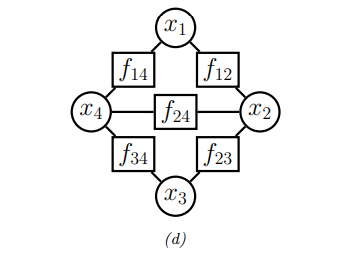
其表示为： \[f(x_1, x_2, x_3, x_4) = f_{14}(x_1, x_4) f_{12}(x_1, x_2) f_{34}(x_3, x_4) f_{23}(x_2, x_3) f_{24}(x_2, x_4)\] 因此，通过因子图的表示法，我们可以更精确地控制变量之间的关系。

有向概率图模型也可以转换为因子图。每个条件概率分布（CPD）被转换为一个因子，并连接到使用该 CPD 的所有变量。下面是一个例子：

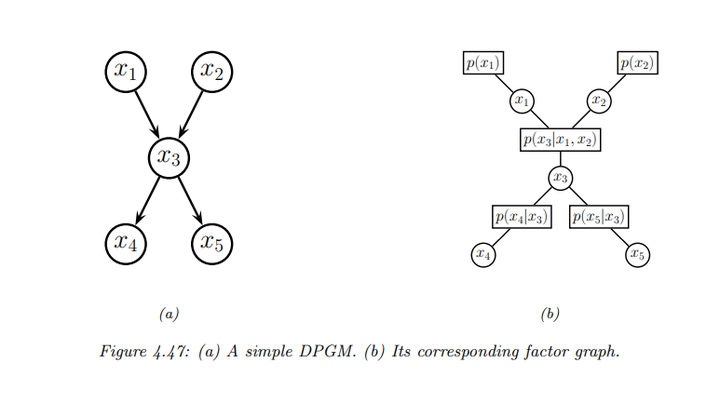
\[f(x_1, x_2, x_3, x_4, x_5) = f_1(x_1) f_2(x_2) f_{123}(x_1, x_2, x_3) f_{34}(x_3, x_4) f_{35}(x_3, x_5)\]

其中，因子\(f_{123}(x_1, x_2, x_3)\)代表条件概率\(p(x_3|x_1, x_2)\)等。

1.2 Forney因子图（Forney Factor Graphs, FFG）

Forney因子图也叫做标准因子图，与双部因子图不同的是：

• 节点表示因子。
• 边表示变量。变量与多个因子通过边关联。

例子解释

假设有如下因子化的函数：

\[f(x_1, ..., x_5) = f_a(x_1) f_b(x_1, x_2) f_c(x_2, x_3, x_4) f_d(x_4, x_5)\]

该函数的 Forney 因子图如图所示

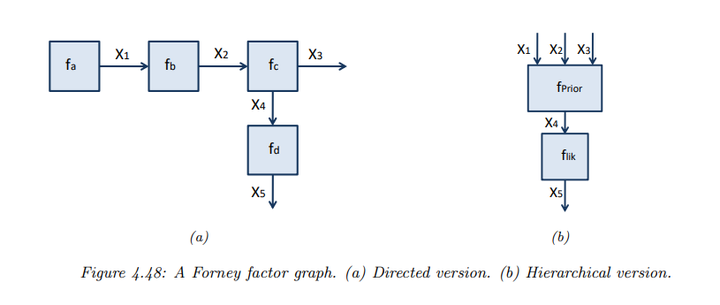
每条边代表变量。例如，\(x_3\)​ 只参与一个因子\(f_c\)，并且它只连接到一个节点，这叫做“半边”（half-edge）。这种表示方法非常适合表示某些有自然生成顺序的变量（如时间序列）。

FFG 还有一种表示来支持层次（组成）结构，即可以将复杂的变量依赖结构表示为一个黑盒。例如，如上图的(b) 展示了一个层次结构的示例，其中因子\(f_{prior}(x_1, x_2, x_3, x_4)\)代表复杂的联合分布，因子\(f_{lik}(x_4, x_5)\)代表似然函数。

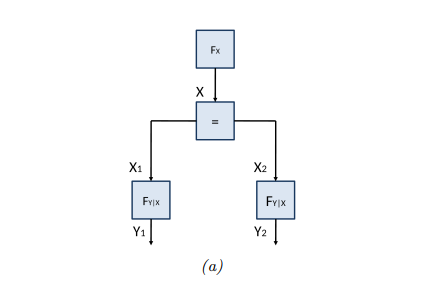
当变量需要参与超过两个因子时，还可以引入等式约束节点。例如上图 展示了如何将多个变量通过等式约束节点连接。这个约束的作用是确保所有连接到该因子的变量具有相同的值，其形式化定义如下：

\[f_=(x, x_1, x_2) = \delta(x - x_1) \delta(x - x_2)\]

这里，\(\delta(u)\)是 Dirac delta 函数（若\(u\)是连续的）或 Kronecker delta 函数（若\(u\)是离散的），用于确保连接到此因子的变量值相等。

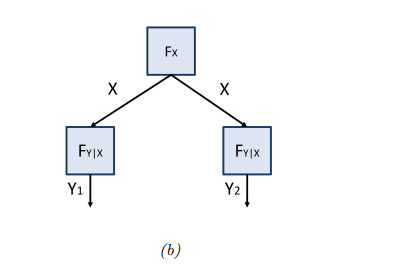
上图显示了等式约束节点的简化表示，这里我们使用变量\(x\)在多个因子之间共享，确保它们的值一致。我们可以将因子\(f_{y|x}(y, x)\)视为条件概率\(p(y|x)\)，并将相同的因子重复使用，这也是一种参数共享（parameter tying）。

六、结构因果模型（Structural Causal Models, SCM）

传统的概率模型只能用于描述世界的静态关系，而因果模型可以用于描述世界发生变化时的影响，允许我们进行干预并推断这些干预的效果。通过干预某个变量，因果模型能够预测系统中的其他变量如何受到影响。

一个SCM被定义为三元组\(M = (U, V, F)\)：

\(U = \{ U_i : i = 1, \ldots, N \}\)：“噪声”变量的集合，作为模型的输入。 \(V = \{ V_i : i = 1, \ldots, N \}\)：内生变量的集合，属于模型自身。 *\(F = \{ f_i : i = 1, \ldots, N \}\)：一组确定性函数，形式为：\(V_i = f_i(V_, U_i)\)其中\(pa_i\)是变量\(i\)的父节点，\(U_i \in U\)是外部输入。

SCM 假设所有的因果相关因素都被包含在模型中，这被称为“因果马尔科夫假设”，即模型中的噪声项\(U\)是相互独立的。如果噪声项之间存在依赖关系，可以通过引入隐藏的父节点来表示这些依赖关系。

1. 示例：教育对财富的因果影响

以教育水平（X）对财富（Y）的影响为例

\(X\)：表示个人的教育水平，可以用一个数字来表示（例如，0 = 高中，1 = 大学，2 = 研究生）。

\(Y\)：表示某一时刻的财富水平。

\(Z\)：表示因教育所产生的债务。

在一些情况下，增加教育水平\(X\)可能会导致财富\(Y\)的增加。这种情况下，从\(X\)到\(Y\)的边被添加。

然而，接受更多教育可能会产生大量费用（在某些国家），这可能会对财富产生干扰作用。因此，从\(X\)到\(Z\)的边被添加，以反映教育水平增加通常伴随的债务增加。

同时，从\(Z\)到\(Y\)的边被添加，表示债务的增加通常会导致财富的减少。

图形表示如下，通过有向边表示变量之间的因果关系：

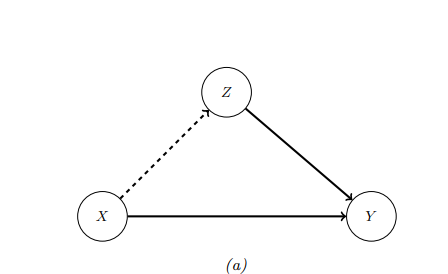
对应的SCM形式为：

\[X = f_X(U_x)\]

\[Z = f_Z(X, U_z)\]

\[Y = f_Y(X, Z, U_y)\]

其中\(f_X, f_Y, f_Z\)是某组函数，\(U_x, U_y, U_z\)​ 是噪声变量。

我们还可以明确表示噪声项，这清楚地表明了噪声项在先验上是独立的。

2. 结构方程模型（Structural equation models）

SEM 是 SCM 的一个特例，其中所有的函数关系都是线性的，噪声项服从高斯分布。这种模型在经济学和社会科学中常用，因为它建模了因果关系，并且计算上较为简单。例如前面例子：

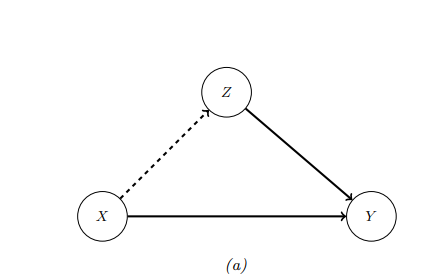
这里我们可以用SEM表示为：

\[X = U_x\]

\[Z = c_z + w_{xz}X + U_z\]

\[Y = c_y + w_{xy}X + w_{zy}Z + U_y\]

这里，\(c\)是常数项，\(w\)是权重，\(U\)是外生噪声。

假设噪声项服从高斯分布：

\[p(U_x) = N(U_x | 0, \sigma^2_x)\]

\[p(U_z) = N(U_z | 0, \sigma^2_z)\]

\[p(U_y) = N(U_y | 0, \sigma^2_y)\]

则模型可以转换为高斯的有向图模型：

\[p(X) = N(X | \mu_x, \sigma^2_x)\]

\[p(Z|X) = N(Z | c_z + w_{xz}X, \sigma^2_z)\]

\[p(Y|X, Z) = N(Y | c_y + w_{xy}X + w_{zy}Z, \sigma^2_y)\]

3. SCM的干预操作（Do operator）

干预指的是改变一个或多个局部机制的行为。例如，可以强制某个变量达到特定值，记作\(\text{do}(X_i = x_i)\)。这意味着我们强制将变量\(X_i\)​ 的值设置为\(x_i\)。当进行完美干预时，应“切断”指向\(X_i\)的边，表示该变量的值现在独立于其通常的父节点。这种操作称为“图形手术（graph surgery）”。

使用教育模型作为例子，可以通过强制\(Z\)为某个值（例如，支付所有人的学生贷款）来进行干预。此时，条件概率\(p(X | \text{do}(Z = z))\)和\(p(X | Z = z)\)是不同的，因为干预改变了模型。

如果我们看到某人没有债务，可能推断他们没有接受高等教育（即\(p(X \geq 1 | Z = 0)\)较小）。但如果我们实施了干预（如免除所有人的学生贷款），那么观察到某人没有债务不会影响我们对其教育背景的看法（即\(p(X \geq 1 | do(Z = 0)) = p(X \geq 1)\)）。

在更现实的场景中，可能无法将变量设置为特定值，但可以从当前值出发进行某种程度的改变。例如，可能会将每个人的债务减少一个固定的金额\(\Delta = -10,000\)。这可以表示为：\(Z = f'_Z(Z, U_z)\)其中\(f'_Z(Z, U_z) = f_Z(Z, U_z) + \Delta\)。

为了建模这类情景，除了上面对模型图进行修改外，我们也可以在原图上创建一个增强DAG，其中每个变量都增加了一个额外的父节点，表示该变量的机制是否以某种方式改变。在增强DAG中，可以使用标准的概率推断进行条件计算。例如：\(p(Q | \text{do}(A_z = a), E = e) = p(Q | A_z = a, E = e)\)

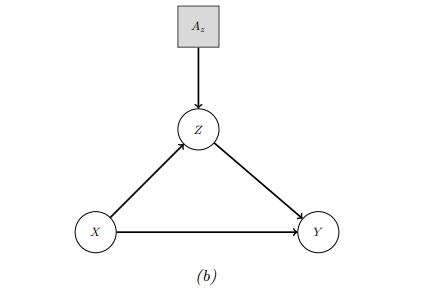
4. 反事实推理（Counterfactuals）

反事实推理关注的是结果的原因。例如，在服用阿司匹林后，如果头痛消失，可能会问：“如果我没有服用阿司匹林，我的头痛是否仍然会消失？”Judea Pearl 据此提出了因果层次结构，包括三个分析层次，每个层次的假设越来越强，具体如下：

反事实预测过程包括：

• 反推：推断给定证据的潜在因素分布\(p(U_i | A_i = a, Y_i = y_i)\)。
• 干预：在结构因果模型中修改因果机制，将\(A_i = a\)替换为\(A_i = a'\)。
• 预测：通过修改后的模型计算\(p(Y_{a'} | A_i = a, Y_i = y_i)\)。

简单来说就是先根据观测结果得到潜在变量的分布，然后在这个潜在变量的分布的基础上，进行do operation并计算结果的分布。