[Probabilistic Machine Learning]: Fundamentals-Information theory

一、KL散度

机器学习本质上是对信息的处理，其中一个关键就在于如何衡量从一个信息的分布到另一个信息分布的差别与变化。KL 散度（Kullback-Leibler Divergence）作为衡量分布差异的最经典函数，其定义为：

• 离散情况：

\[D_{KL}(p \| q) \equiv \sum_{k=1}^{K} p_k \log \frac{p_k}{q_k}\]

连续情况：

\[D_{KL}(p \| q) \equiv \int dx \, p(x) \log \frac{p(x)}{q(x)}\]

1. KL 散度满足的性质

1.1 连续性

KL 散度在其参数上是连续的，除非\(p_k\)​ 或\(q_k\)​ 为零。如果\(p\)趋近于零，满足：

\[\lim_{p \to 0} \frac{p \log p}{q} = 0\]

这保证了当\(p = 0\)时，函数仍然连续。然而，当\(q = 0\)且\(p > 0\)时，更新的幅度将趋向于无限。

1.2 非负性

KL 散度总是非负的：

\[D_{KL}(p \| q) \geq 0\]

当且仅当\(p = q\)时，KL 散度等于零。证明使用 Jensen 不等式：

\[f\left(\sum_{i=1}^{n} \lambda_i x_i\right) \leq \sum_{i=1}^{n} \lambda_i f(x_i)\]

通过推导，可以得到：

\[\begin{align*} -D_{KL}(p \| q) &= -\sum_{x \in A} p(x) \log \frac{p(x)}{q(x)} \\&\leq \log \left(\sum_{x \in A} \frac{q(x)}{p(x)}p(x)\right)\\ &\leq \log 1 = 0 \end{align*}\]

非负性方便我们明确优化的目标。

Not Found

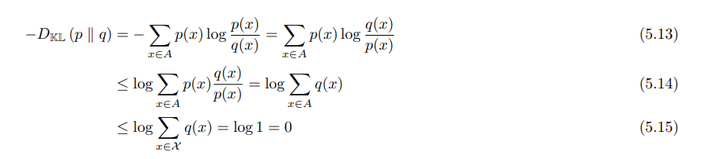
1.3 重参数化不变性

KL 散度在随机变量的任意可逆变换下保持不变。如果将随机变量从\(x\)变换为\(y = f(x)\)，则有：

\[p(x) \, dx = p(y) dy\] \[q(x) \, dx = q(y)\]

那么 KL 散度可以写成：

\[D_{KL}(p(x) \| q(x)) = \int dx \, p(x) \log \frac{p(x)}{q(x)}\]

通过变换得到：

\[= \int dy \, p(y) \log \left( \frac{p(y)}{q(y)} \cdot \frac{dy}{dx} \cdot \frac{dx}{dy} \right)\]

由于\(p(y) dy = p(x) dx\)和\(q(y) dy = q(x) dx\)，可以得到：

\[D_{KL}(p(x) \| q(x)) = D_{KL}(p(y) \| q(y))\]

因此，KL 散度在重参数化下是保持不变的。这表明 KL 散度是关于分布本身的，而不是表示空间的方式。

Not Found

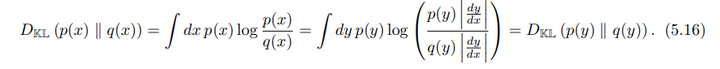
1.4 对均匀分布的单调性

从\(N\)个元素的均匀分布更新到\(N'\)个元素的均匀分布，KL 散度为：

\[D_{KL}(p \| q) = \sum_{k} \frac{1}{N'} \log \frac{1/N'}{1/N} = \log \frac{N}{N'}\]

这表明更新的幅度与元素数量的比例相关。

1.5 KL 散度的链式法则

KL 散度满足链式法则：

\[D_{KL}(p(x, y) \| q(x, y)) = \int dx \, dy \, p(x, y) \log \frac{p(x, y)}{q(x, y)}\]

可以分解为：

\[D_{KL}(p(x) \| q(x)) + E_{p(x)}\left[D_{KL}(p(y|x) \| q(y|x))\right]\]

条件 KL 散度 定义为：

\[D_{KL}(p(y|x) \| q(y|x)) \equiv \int dx \, p(x) \int dy \, p(y|x) \log \frac{p(y|x)}{q(y|x)}\]

此外我们注意到：

\[D_{KL} (p(x,y) \| q(x,y)) \geq D_{KL} (p(y) \| q(y))\]

对这一结果的一种直观解释是，如果只部分观察随机变量，那么区分两个候选分布比观察全部随机变量更难。

Not Found

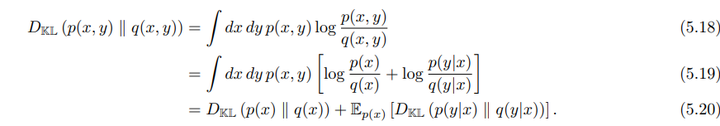
2. Thinking about KL

在这一节中，我们主要讨论 KL 散度的一些特性。

2.1 KL 散度的单位

KL 散度的单位与我们选择的对数的底数有关。对数的不同底数之间的差异只是一个乘法常数的差异，因此 KL 散度的计算方式类似于选择测量信息的单位：

• 当使用底为 2 的对数时，KL 散度的单位为比特（bits），即“二进制数字”。
• 当使用自然对数（通常用于数学方便）时，单位为纳特（nats），即“自然单位”。

为了在这两种单位之间进行转换，我们有\(\log_2 y = \frac{\log y}{\log 2}\)，因此：

\[1 \text{ bit} = \log_2 \text{ nats} \sim 0.693 \text{ nats}\]

\[1 \text{ nat} = \frac{1}{\log_2} \text{ bits} \sim 1.44 \text{ bits}\]

2.2 KL 散度的非对称性

KL 散度在其两个参数中不是对称的。尽管看起来非常不合理，但实际上非对称性源于我们要求自然链式法则。在分解分布时，我们需要对被条件化的变量取期望。在 KL 散度中，我们是对第一个参数\(p(x)\)取期望，这打破了两个分布之间的对称性。

从更直观的角度来看，从分布\(q\)更新到\(p\)所需的信息量通常与从\(p\)更新到\(q\)所需的信息量不同。例如，考虑两个 Bernoulli 分布：

• 第一个分布成功的概率为 0.443；
• 第二个分布成功的概率为 0.975。

计算这两个分布之间的 KL 散度：

\[\begin{align*} D_{KL}(p \| q) &= 0.975 \log \frac{0.975}{0.443} + 0.025 \log \frac{0.025}{0.557} \\&= 0.692 \text{ nats} \sim 1.0 \text{ bits} \end{align*}\]

这表明，从分布\([0.443, 0.557]\)更新到\([0.975, 0.025]\)需要 1 比特的信息。

反过来：

\[\begin{align*} D_{KL}(q \| p) &= 0.443 \log \frac{0.443}{0.975} + 0.557 \log \frac{0.557}{0.025} \\&= 1.38 \text{ nats} \sim 2.0 \text{ bits} \end{align*}\]

这表明，从分布\([0.975, 0.025]\)更新到\([0.443, 0.557]\)需要 2 比特的信息。由此可见，从一个接近均匀的分布到几乎确定的分布需要大约 1 比特的信息，而从近乎确定的结果转变到类似于抛硬币的结果则需要更多的信息。

2.3 KL 散度作为evidence的期望权重

假设你有两个不同的假设\(P\)和\(Q\)，并希望在它们之间选择。你收集了一些数据\(D\)。贝叶斯定理告诉我们：

\[Pr(P|D) = \frac{Pr(D|P) \cdot Pr(P)}{Pr(D)}\]

通常，这需要评估边际似然\(Pr(D)\)，这在计算上是困难的。如果我们考虑两个假设的概率比率：

\[\frac{Pr(P|D)}{Pr(Q|D)} = \frac{Pr(D|P)}{Pr(D|Q)} \cdot \frac{Pr(P)}{Pr(Q)}\]

边际似然\(Pr(D)\)被消去。取对数后结果如下：

\[\log \frac{Pr(P|D)}{Pr(Q|D)} = \log \frac{p(D)}{q(D)} + \log \frac{Pr(P)}{Pr(Q)}\]

后验对数概率比率只是先验对数概率比率加上 I. J. Good 所称的evidence权重\(D\)：

\[w[P/Q; D] \equiv \log \frac{p(D)}{q(D)}\]

在这种解释下，KL 散度就是在假设\(P\)为真时，每次观察提供的\(P\)相对于\(Q\)的evidence的期望。

3. 最小化KL散度

在具体问题时，我们往往需要对KL散度进行最小化。

3.1 正向与反向 KL

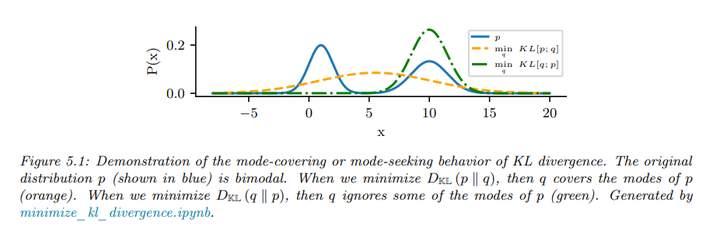
KL 散度的非对称性意味着，通过最小化\(D_{KL}(p \| q)\)（也称为正向 KL ）来寻找一个接近于\(p\)的分布\(q\)，与通过最小化\(D_{KL}(q \| p)\)（也称为反向 KL ）来寻找\(q\)会有一定区别。

示例： 考虑一个双峰分布\(p\)，我们用一个单峰高斯分布\(q\)来近似。为了防止\(D_{KL}(p \| q)\)变为无穷大，我们必须当\(p > 0\)时有\(q > 0\)（即\(q\)必须在\(p\)的每个非零点上都有支持），因此\(q\)会覆盖两个峰，这称为模式覆盖（mode-covering）或零避免行为（orange curve）。相反，为了防止\(D_{KL}(q \| p)\)变为无穷大，我们必须有\(q = 0\)当\(p = 0\)时，这会导致模式追寻（mode-seeking）或零强制行为（green curve）。

Not Found

3.2 矩（Moment）投影（模式覆盖）

当我们通过最小化正向 KL 来计算\(q\)时：

\[q = \arg \min_q D_{KL}(p \| q)\]

我们不妨假设\(q\)是一种指数族分布：

\[q(x) = h(x) \exp\left[\eta^T T(x) - \log Z(\eta)\right]\]

最优性的一阶条件如下：

\[\frac{\partial \eta_i D_{KL}(p \| q)}{\partial \eta_i} = -\frac{\partial \eta_i}{\partial \eta_i} \int p(x) \log q(x) dx\]

继续推导可得：

\[\begin{align*} \partial_{\eta_i} D_{KL}(p \| q) &= -\partial_{\eta_i} \int p(x) \log q(x) \, dx \\ &= -\partial_{\eta_i} \int p(x) \left( \eta^T T(x) - \log Z(\eta) \right) \, dx \\ &= -\partial_{\eta_i} \int \left( p(x) T_i(x) \, dx - E_{q(x)}[T_i(x)] \right)dx \\ &= -E_{p(x)}[T_i(x)] + E_{q(x)}[T_i(x)] = 0 \end{align*}\]

可以看到，当梯度为0时候，最优的\(q\)匹配\(p\)的矩，因此该过程称为矩匹配（moment matching）。这种优化被称矩投影（M-projection）。

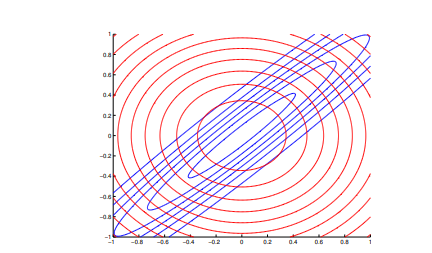
示例： 假设真实目标分布\(p\)是一个相关的二维高斯分布：

\[p(x) = N(x|\mu, \Sigma) = N(x|\mu, \Lambda^{-1})\]

我们将其近似为一个由两个一维高斯分布组成的分布\(q\)：

\[q(x|m, V) = N(x_1|m_1, v_1) N(x_2|m_2, v_2)\]

进行矩匹配后，最优的\(q\)形状为：

\[q(x) = N(x_1|\mu_1, \Sigma_{11}) N(x_2|\mu_2, \Sigma_{22})\]

如下图所示，结果分布\(q\)覆盖了\(p\)，即模式覆盖。

Not Found

3.3 信息（Information）投影（模式追寻）

现在假设我们通过最小化反向 KL 来计算\(q\)：

\[q = \arg \min_q D_{KL}(q \| p)\]

这称为信息投影（I-projection）。这个优化问题通常更容易计算，因为目标需要对\(q\)进行期望计算，而我们可以选择一个可处理的分布族。

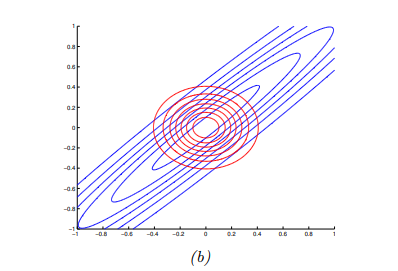
示例： 考虑真实分布是一个全协方差高斯分布：

\[p(x) = N(x|\mu, \Lambda^{-1})\]

并让\(q\)为对角高斯分布：

\[q(x) = N(x|m, \text{diag}(v))\]

可以证明，最优的变分参数为：

\[m = \mu\] \[v_i = \Lambda^{-1}_{ii}\]

证明过程如下：

如下图所示，我们看到后验方差过于狭窄，即近似后验过于自信。然而，值得注意的是，最小化反向 KL 并不总是导致过于紧凑的近似。

Not Found

4. KL 散度的重要性质

4.1 压缩引理（Compression lemma）

一个KL散度的重要的通用结论是压缩引理，其指出，对于任何分布\(P\)和\(Q\)，以及在这些分布的定义域上定义的标量函数\(ϕ\)，都有以下不等式：

\[E_P[ϕ] \leq \log E_Q\left[e^{ϕ}\right] + D_{KL}(P \| Q)\]

证明过程：

考虑分布\(g(x)\)：
\[g(x) = \frac{q(x)}{Z} e^{ϕ(x)}\]

其中\(Z\)是分区函数：
\[Z = \int dx \, q(x) e^{ϕ(x)}\]

计算\(D_{KL}(P \| G)\)：
\[D_{KL}(P \| G) = D_{KL}(P \| Q) - E_P[ϕ(x)] + \log(Z) \geq 0\]

压缩引理的另一种形式是 Donsker-Varadhan 变分表示：

\[D_{KL}(P \| Q) = \sup_{ϕ} \left( E_P[ϕ(x)] - \log E_Q\left[e^{ϕ(x)}\right] \right)\]

这样我们便为KL散度提供了一个下界。

4.2 KL 散度的数据处理不等式（Data processing inequality for KL）

数据处理不等式表明，任何对来自两个不同分布的样本进行处理的操作都会使这两个样本趋向彼此。具体来说，考虑两个不同的分布\(p(x)\)和\(q(x)\)，通过概率通道\(t(y|x)\)处理后，得到的分布满足：

\[D_{KL}(p(x) \| q(x)) \geq D_{KL}(p(y) \| q(y))\]

证明过程：

\[\begin{align*} D_{KL} (p(x) \| q(x)) &= \int dx \, p(x) \log \frac{p(x)}{q(x)} \\ &= \int dx \, \int dy \, p(x) t(y|x) \log \frac{p(x) t(y|x)}{q(x) t(y|x)} \\ &= \int dx \, \int dy \, p(x, y) \log \frac{p(x, y)}{q(x, y)} \\ &= -\int dy \, p(y) \int dx \, p(x|y) \log \frac{q(x, y)}{p(x, y)} \\ &\geq - \int dy \, p(y) \log \left( \int dx \, p(x|y) \frac{q(x, y)}{p(x, y)} \right) \\ &= - \int dy \, p(y) \log \left( \frac{q(y)}{p(y)} \int dx \, q(x|y) \right) \\ &= \int dy \, p(y) \log \frac{p(y)}{q(y)} \\&= D_{KL} (p(y) \| q(y)) \end{align*}\]

数据处理不等式表明，对随机样本的任何处理都会使这两个分布更难以区分，即这样导致了信息的损失。

5. KL散度与最大似然估计

目标：我们希望找到一个分布\(q\)，使其与真实分布\(p\)的KL散度最小化：
\[q^* = \arg \min_q D_{KL}(p \| q) =\arg \min_q (\int p(x) \log p(x) dx - \int p(x) \log q(x) dx)\]

经验分布：\(p\)是经验分布\(p_D\)​指的是它只在观察到的训练数据上有概率，其余地方为零：
\[p_D(x) = \frac{1}{N} \sum_{n=1}^N \delta(x - x_n)\]

其中\(\delta\)是狄拉克函数。

利用狄拉克函数的特性，可以推导出：
\[D_{KL}(p_D \| q) = -\int p_D(x) \log q(x) dx + C = -\frac{1}{N} \sum_{n} \log q(x_n) + C\]

这里\(C\)是与\(q\)无关的常数。

可以将上述推导重写为：
\[D_{KL}(p_D \| q) = H_{ce}(p_D, q) - H(p_D)\]

其中\(H_{ce}\)​ 是交叉熵，定义为：
\[H_{ce}(p, q) = -\sum_k p_k \log q_k\]

​交叉熵\(H_{ce}(p_D, q)\)是在训练集上评估\(q\)的平均负对数似然。

所以最小化KL散度与经验分布的过程等价于最大化似然，这意味着我们在训练过程中希望找到一个能很好地拟合训练数据的分布。

基于似然的训练方法过于依赖训练集。经验分布仅在有限的数据点上有概率质量，而在其它地方为零，这可能导致对真实分布的不合理假设。即使数据集很大，实际数据来源的空间通常更大，因此需要通过在“相似”输入之间共享概率质量来平滑经验分布。

6. KL散度与贝叶斯推断

贝叶斯推断可以被看作是一个特定的最小化问题，目标是使得新的联合分布\(p(\theta, D)\)尽可能接近先验分布\(q(\theta, D)\)，同时满足已知数据\(D_0\)​ 的约束条件：

\[p(\theta, D) = \arg\min D_{KL}(p(\theta, D) \| q(\theta, D)) \quad \text{subject to} \quad p(D) = \delta(D - D_0)\]

这里\(\delta(D - D_0)\)是一个将所有质量集中在数据集\(D_0\)​ 上的狄拉克分布。

将KL散度写成链式法则的形式，可以得出：

\[D_{KL}(p(\theta, D) \| q(\theta, D)) = D_{KL}(p(D) \| q(D)) + D_{KL}(p(\theta|D) \| q(\theta|D))\]

根据贝叶斯公式，我们有：

\[q(\theta, D) = q(D)q(\theta|D) = q(\theta)q(D|\theta) \Rightarrow q(\theta|D) = \frac{q(D|\theta) q(\theta)}{q(D)}\]

这里注意到\(q(\theta|D)\)与\(q(D|\theta), q(\theta), q(D)\)之间的关系，但它们都是同一分布的不同表示。

通过KL散度的链式法则，更新后的条件分布保持不变：

\[p(\theta|D) = q(\theta|D)\]

然而，关于参数的边际信念则会发生变化：

\[p(\theta) = \int dD \, p(D)q(\theta|D)= ∫dDδ(D−D_0​)q(θ∣D)=q(θ∣D=D_0​)\]

这正是我们在观察到数据时，从先验信念更新得到的后验分布

这一更新过程的一个自然扩展是，如果我们有额外的测量误差，而这些误差是可理解的，那么我们不应将更新的信念完全依赖于观察数据的狄拉克函数，而应使用一个我们理解的分布\(p(D)\)。例如，我们可能不确切知道数据的精确值，但相信经过测量后，它呈现某种均值和标准差的高斯分布。

通过这种方式，参数的条件分布保持不变，但参数的边际概率则更新为：

\[p(\theta) = \int dD \, p(D)q(\theta|D)\]

这个贝叶斯规则的广义形式有时被称为Jeffrey的条件化规则。

7. KL散度与指数族

对于一个具有自然参数\(\eta\)、基础测度\(h(x)\)和充分统计量\(T(x)\)的指数族分布\(p(x)\)表示为：
\[p(x) = h(x) \exp\left[\eta^T T(x) - A(\eta)\right]\]

其中，\(A(\eta) = \log Z\)是对数分区函数，定义为：
\[A(\eta) = \log \int h(x) \exp(\eta^T T(x)) dx\]

对于同一指数族中的两个分布\(p(x|\eta_1)\)和\(p(x|\eta_2)\)，KL散度的闭式解为：
\[D_{KL}(p(x|\eta_1) \| p(x|\eta_2)) = E_{\eta_1}\left[(\eta_1 - \eta_2)^T T(x) - A(\eta_1) + A(\eta_2)\right]\]

或者用期望表示为：
\[= (\eta_1 - \eta_2)^T \mu_1 - A(\eta_1) + A(\eta_2)\]

其中\(\mu_j = E_{\eta_j}[T(x)]\)。

两个高斯分布的KL散度

对于两个多元高斯分布\(N(x|\mu_1, \Sigma_1)\)和\(N(x|\mu_2, \Sigma_2)\)，KL散度为：

\[D_{KL}(N(x|\mu_1, \Sigma_1) \| N(x|\mu_2, \Sigma_2)) = \frac{1}{2}\left[\text{tr}(\Sigma_2^{-1} \Sigma_1) + (\mu_2 - \mu_1)^T \Sigma_2^{-1} (\mu_2 - \mu_1) - D + \log\left(\frac{\det(\Sigma_2)}{\det(\Sigma_1)}\right)\right]\]

在标量情况下：

\[D_{KL}(N(x|\mu_1, \sigma_1) \| N(x|\mu_2, \sigma_2)) = \log\left(\frac{\sigma_2}{\sigma_1}\right) + \frac{\sigma_1^2 + (\mu_1 - \mu_2)^2}{2\sigma_2^2} - \frac{1}{2}\]

8. 使用Fisher信息矩阵近似KL散度

设\(p_\theta(x)\)和\(p_{\theta'}(x)\)是两个分布，其中\(\theta' = \theta + \delta\)。KL散度可以表示为：
\[D_{KL}(p_\theta \| p_{\theta'}) = E_{p_\theta(x)}\left[\log p_\theta(x) - \log p_{\theta'}(x)\right]\]

使用二阶泰勒展开进行近似：
\[D_{KL}(p_\theta \| p_{\theta'}) \approx -\delta^T E\left[\nabla \log p_\theta(x)\right] - \frac{1}{2} \delta^T E\left[\nabla^2 \log p_\theta(x)\right] \delta\]

由于期望评分函数为零（第一项为0），我们得到：
\[D_{KL}(p_\theta \| p_{\theta'}) \approx \frac{1}{2} \delta^T F(\theta) \delta\]

其中，Fisher信息矩阵定义为：
\[F = -E\left[\nabla^2 \log p_\theta(x)\right] = E\left[(\nabla \log p_\theta(x))(\nabla \log p_\theta(x))^T\right]\]

9. 与Bregman散度的关系

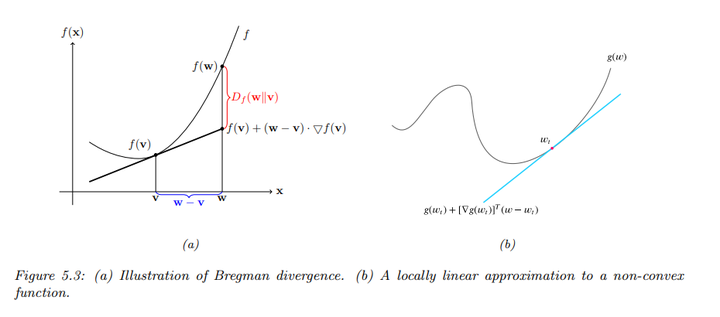
设\(f : \Omega \to \mathbb{R}\)是一个在闭凸集\(\Omega\)上连续可微且严格凸的函数，Bregman散度定义为：
\[B_f(w \| v) = f(w) - f(v) - (w - v)^T \nabla f(v)\]

这个定义可以理解为一个非线性度量，度量了点\(w\)与点\(v\)之间的距离。

引入函数的线性近似：
\[\hat{f}_v(w) = f(v) + (w - v)^T \nabla f(v)\]

Bregman散度实际上是实际值与线性近似值之间的差：
\[B_f(w \| v) = f(w) - \hat{f}_v(w)\]

由于\(f\)是凸函数，因此有\(B_f(w \| v) \geq 0\)。

如果\(f(w) = \|w\|^2\)，则\(B_f(w \| v) = \|w - v\|^2\)表示平方欧几里得距离。

如果\(f(w) = w^T Q w\)，则Bregman散度表示为平方Mahalanobis距离。

如果\(w\)是指数族分布的自然参数，且\(f(w) = \log Z(w) = A(w)\)，则Bregman散度等同于KL散度。

\[\begin{align*} B_f(\eta_q \| \eta_p) &= A(\eta_q) - A(\eta_p) - (\eta_q - \eta_p)^T \nabla_{\eta_p} A(\eta_p) \\ &= A(\eta_q) - A(\eta_p) - (\eta_q - \eta_p)^T E_p[T(x)] \\ &= D_{KL}(p \| q) \end{align*}\]

Not Found

二、熵

1. 离散随机变量的熵

离散随机变量\(X\)的熵\(H(X)\)定义为：

\[H(X) \equiv -\sum_{k=1}^{K} p(X = k) \log p(X = k) = -E_X[\log p(X)]\]

熵也可以用不同的对数底数表示，常用的是底数为 2（单位为 bits）或底数为\(e\)（单位为 nats）。熵可以表示为与均匀分布之间的 KL 散度的关系：

\[H(X) = \log K - D_{KL}(p(X) \| u(X))\]

其中与均匀分布\(u(X)\)的 KL 散度为：

\[D_{KL}(p(X) \| u(X)) = \sum_{k=1}^{K} p(X = k) \log p(X = k) - \frac{1}{K}\]

因此，如果\(p\)是均匀分布，KL 散度为零，熵达到最大值\(\log K\)。

特别的，对于二元随机变量\(X \in \{0, 1\}\)，我们可以表示为：

\[H(X) = -[p(X = 1) \log p(X = 1) + p(X = 0) \log p(X = 0)]\]

即：

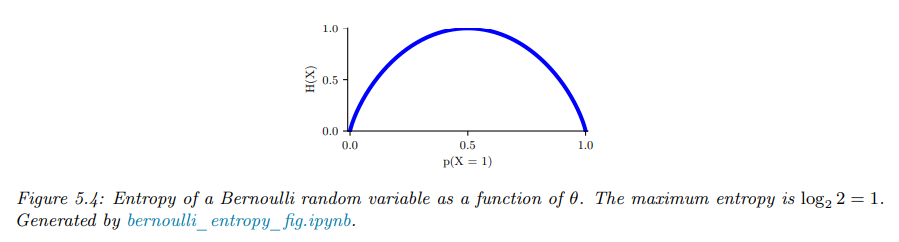
\[H(X) = -[\theta \log \theta + (1 - \theta) \log(1 - \theta)]\]

这被称为二元熵函数\(H(\theta)\)。

Not Found

2. 连续随机变量的微分熵

对于连续随机变量\(X\)及其概率密度函数\(p(x)\)，微分熵定义为：

\[h(X) \equiv -\int_X dx \, p(x) \log p(x)\]

例如，\(d\)维高斯分布的熵为：

\[h(N(\mu, \Sigma)) = \frac{1}{2} \log |2\pi e \Sigma| = \frac{d}{2} + \frac{d}{2} \log(2\pi) + \frac{1}{2} \log |\Sigma|\]

在一维情况下：

\[h(N(\mu, \sigma^2)) = \frac{1}{2} \log(2\pi e \sigma^2)\]

需要注意的是，与离散情况不同，微分熵可以为负值，因为概率密度函数可以大于1。

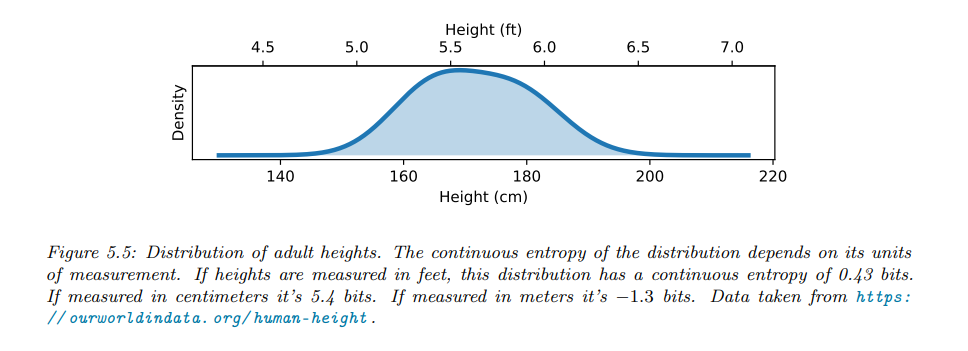
微分熵可以通过量化的有限精度来理解。可以证明，对于连续随机变量\(X\)的\(n\)位量化，熵近似为：

\[h(X) + n\]

以均匀分布为例子：

Not Found

此外，微分熵缺乏重参数不变性。例如，如果我们变换随机变量\(y = f(x)\)，熵将会变换：

\[p(y) dy = p(x) dx \Rightarrow p(y) = p(x) \left|\frac{dy}{dx}\right|^{-1}\]

因此，微分熵变换为：

\[h(X) = -\int dx \, p(x) \log p(x) = h(Y) - \int dy \, p(y) \log \left|\frac{dy}{dx}\right|\]

这意味着，即使是简单的单位转换也会改变微分熵的值。

Not Found

3 典型集

概率分布的典型集是信息内容接近于从该分布随机样本的期望信息内容的元素集合。更具体地，对于支持\(x \in X\)的分布\(p(x)\)，定义\(\epsilon\)-典型集\(A^{N}_{ϵ} \subseteq X^N\)为：

\[H(p(x)) - ϵ \leq -\frac{1}{N} \log p(x_1, \ldots, x_N) \leq H(p(x)) + ϵ\]

如果我们假设\(p(x_1, \ldots, x_N) = \prod_{n=1}^{N} p(x_n)\)，则中间项可以解释为 N-sample 的经验熵估计。渐近均分性质（AEP）表明，随着\(N \to \infty\)，这个值（在概率上）会收敛到真实的熵。因此，典型集的概率接近于 1，从而成为从\(p(x)\)生成的结果的compact summary。

4. 交叉熵和困惑度

模型分布\(q\)与真实分布\(p\)之间距离的标准方法是 KL 散度：

\[D_{KL}(p \| q) = \sum_{x} p(x) \log \frac{p(x)}{q(x)} = H_{ce}(p, q) - H(p)\]

其中，交叉熵\(H_{ce}(p, q)\)定义为：

\[H_{ce}(p, q) = -\sum_{x} p(x) \log q(x)\]

而\(H(p) = H_{ce}(p, p)\)是熵，它是与模型无关的常数。

在语言建模中，通常报告的替代性能度量称为困惑度，定义为：

\[\text{perplexity}(p, q) \equiv 2^{H_{ce}(p, q)}\]

可以通过以下方式计算交叉熵的经验近似： 假设我们用基于从\(p\)中采样的数据的经验分布来近似真实分布：

\[p_D(x|D) = \frac{1}{N} \sum_{n=1}^{N} I(x = x_n)\]

在这种情况下，交叉熵为：

\[H = -\frac{1}{N} \sum_{n=1}^{N} \log p(x_n) = -\frac{1}{N} \log \prod_{n=1}^{N} p(x_n)\]

相应的困惑度为：

\[\text{perplexity}(p_D, p) = 2^{-\frac{1}{N} \log\left(\prod_{n=1}^{N} p(x_n)\right)} = \left(\prod_{n=1}^{N} p(x_n)\right)^{-\frac{1}{N}} = \sqrt[N]{\prod_{n=1}^{N} \frac{1}{p(x_n)}}\]

在语言模型中，我们通常在预测下一个单词时考虑前面的单词。例如，在二元模型中，我们使用二阶马尔可夫模型的形式\(p(x_n|x_{n-1})\)。假设模型预测每个单词是同样可能的，而与上下文无关，即\(p(x_n|x_{n-1}) = \frac{1}{K}\)，其中\(K\)是词汇表中的单词数量。此时，困惑度为：

\[\left(\left(\frac{1}{K}\right)^{N}\right)^{-\frac{1}{N}} = K\]

如果某些符号比其他符号更可能，且模型正确反映了这一点，则其困惑度将低于\(K\)。然而，我们有\(H(p^*) \leq H_{ce}(p^*, p)\), 因此我们无法将困惑度降低到\(2^{-H(p^*)}\)之下。

三、 互信息

KL散度告诉了我们如何衡量两个分布之间的区别，而两个分布之间的相关性则需要通过互信息来进行衡量。

1. 定义

互信息\(I(X; Y)\)衡量了随机变量\(X\)和\(Y\)之间的信息增益，定义为：
\[I(X; Y) \equiv D_{KL}(p(x, y) \| p(x)p(y)) = \sum_{y \in Y} \sum_{x \in X} p(x, y) \log \frac{p(x, y)}{p(x)p(y)}\] 很容易看出，互信息是非负的：

\[I(X; Y) = D_{KL}(p(x, y) \| p(x)p(y)) \geq 0\]

当且仅当\(p(x, y) = p(x)p(y)\)时，等号成立。

2. 解释

互信息可以用联合熵和条件熵重新表示：

\[I(X; Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)\]

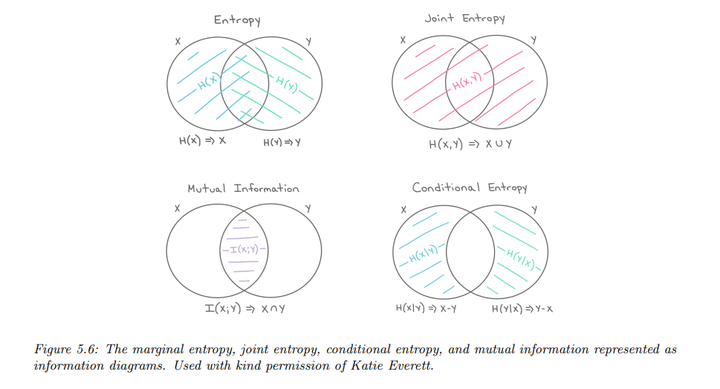
这表明观察\(Y\)后，关于\(X\)的不确定性减少的值，反之亦然。此外，互信息还可以表示为：

\[I(X; Y) = H(X, Y) - H(X|Y) - H(Y|X)\]

或者：

\[I(X; Y) = H(X) + H(Y) - H(X, Y)\]

具体关系可以通过下面的图很直观的展示出来：

Not Found

3 数据处理不等式

数据处理不等式表明，对于未知变量\(X\)，如果我们观察到它的噪声函数\(Y\)，并对噪声观测进行处理以生成新变量\(Z\)，则对未知量\(X\)的信息量不会增加。这可以形式化为：

\[I(X; Y) \geq I(X; Z)\]

证明如下：

\[I(X;Y,Z)=I(X;Z)+I(X;Y∣Z)=I(X;Y)+I(X;Z∣Y)\]

由于\(X \perp Z | Y\)，我们有\(I(X; Z | Y) = 0\)，因此：

\[I(X; Z) + I(X; Y | Z) = I(X; Y)\]

因为\(I(X; Y | Z) \geq 0\)，所以：

\[I(X; Y) \geq I(X; Z)\]

数据处理不等式（Data Processing Inequality, DPI）表明，在一个马尔可夫链\(X \to Y \to Z\)中，关于\(X\)的信息在通过\(Y\)传递到\(Z\)的过程中不会增加。

4. 充分统计量

设有链关系\(\theta \to X \to s(X)\)，其中\(\theta\)是待推断的参数，\(X\)是观测数据，\(s(X)\)是从数据中提取的统计量。通过数据处理不等式，得出\(I(\theta; s(X)) \leq I(\theta; X)\)。这意味着，通过\(s(X)\)获取的信息不可能超过通过\(X\)获取的信息。

当不等式成立为等式时，称\(s(X)\)是\(X\)的充分统计量。也就是说，知道\(s(X)\)就足够推断\(\theta\)，并且从\(s(X)\)可以重建\(X\)。

如果统计量\(s(X)\)包含关于\(\theta\)的所有相关信息，并且不包含冗余信息，则称\(s(X)\)是最小充分统计量。它最大限度地压缩数据，而不丢失与推断\(\theta\)相关的信息。

例如，对于\(N\)次伯努利试验，最小充分统计量是\(N\)和成功次数\(N_1 = n\)（即\(I(X_n = 1)\)）。对于已知方差的高斯分布，推断均值只需知道经验均值和样本数量。

指数族分布是最小充分统计量的代表，因为它们包含的信息仅限于某些统计量的约束。根据 Pitman-Koopman-Darmois 定理，只有在样本数量增加时，才存在具有有限维充分统计量的指数族分布。

5. 多元互信息

多元互信息主要用来衡量一组随机变量之间的相关性。

5.1. 总相关性（Total Correlation）

多元互信息最简单的定义之一是使用总相关性（Total Correlation）或多信息（Multi-Information），定义为：
\[TC(\{X_1, \dots, X_D\}) ≜ D_{KL} \left( p(x) \middle\| \prod_{d} p(x_d) \right)\]

其等价表达式为：
\[TC(\{X_1, \dots, X_D\}) = \sum_{d} H(x_d) - H(x)\]

其中，\(H(x)\)是联合熵，\(H(x_d)\)是边际熵。对三个变量\(X, Y, Z\)，总相关性为：
\[TC(X, Y, Z) = H(X) + H(Y) + H(Z) - H(X, Y, Z)\]

联合熵\(H(X,Y,Z)\)的定义是：
\[H(X, Y, Z) = - \sum_{x, y, z} p(x, y, z) \log p(x, y, z)\]

总相关性描述了所有变量之间的整体依赖关系。如果\(p(x) = \prod_d p(x_d)\)，即变量是独立的，那么总相关性为零。即使只有一对变量是相互依赖的，总相关性也会为正。

5.2. 相互作用信息（Interaction Information, Co-Information）

为了克服总相关性只要任意两个变量相互作用就为正的缺点，可以引入多元互信息（multivariate mutual information (MMI)），也叫做相互作用信息（Interaction Information）或者共信息（Co-Information）。这个定义基于条件互信息的递归定义：
\[I(X_1; \dots ; X_D) = I(X_1; \dots ; X_{D-1}) - I(X_1; \dots ; X_{D-1} | X_D)\]

对于三个变量\(X, Y, Z\)，其定义为：
\[I(X; Y; Z) = I(X; Y) - I(X; Y | Z)\]

这可以解释为：当条件变量\(Z\)已知时，互信息\(I(X;Y)\)的变化。同样，可以写成：
\[I(X; Y; Z) = I(X; Z) - I(X; Z | Y)\] \[I(X; Y; Z) =I(Y; Z) - I(Y; Z | X)\]

这意味着：相互作用信息是两个变量之间的互信息在条件第三个变量已知时的变化。
根据条件互信息的定义，可以推导出：
\[I(X; Z | Y) = I(Z; X, Y) - I(Y; Z)\]

因此，式子可以重新写成：
\[I(X; Y; Z) = I(X; Z) + I(Y; Z) - I(X, Y; Z)\]

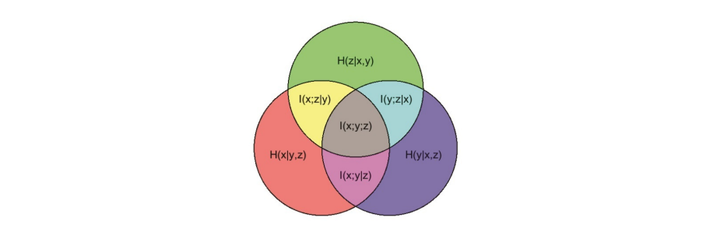
这说明，相互作用信息是变量\(X\)和\(Y\)单独提供的关于\(Z\)的信息与它们联合提供的信息之间的差异。

上面的关系可以通过下面的图来直观展示：

Not Found

5.3. 协同与冗余（Synergy and Redundancy）

相互作用信息\(I(X; Y; Z)\)可以为正、零或负，取决于变量之间的关系：

• 如果\(I(X; Z) + I(Y; Z) > I(X, Y; Z)\)，说明\(X\)和\(Y\)提供了关于\(Z\)的冗余信息，此时\(I(X; Y; Z) > 0\)。
• 如果\(I(X; Z) + I(Y; Z) < I(X, Y; Z)\)，说明联合观察\(X\)和\(Y\)提供了额外的关于\(Z\)的信息，存在协同作用，此时\(I(X; Y; Z) < 0\)。

5.4. 相互作用信息与因果关系（MMI and Causality）

MMI 的符号可以用于区分不同的有向图模型，这些模型有时可以用来解释因果关系。例如：

共同原因模型（Common Cause Model）：例如\(X \leftarrow Z \rightarrow Y\)，其中\(Z\)是\(X\)和\(Y\)的共同原因。此时，条件化在\(Z\)上会使\(X\)和\(Y\)独立，因此\(I(X; Y | Z) \leq I(X; Y)\)，所以\(I(X; Y; Z) \geq 0\)。

共同结果模型（Common Effect Model）：例如\(X \rightarrow Z \leftarrow Y\)，其中\(Z\)是\(X\)和\(Y\)的共同结果。此时，条件化在\(Z\)上会使\(X\)和\(Y\)相关，因此\(I(X; Y | Z) \geq I(X; Y)\)，所以\(I(X; Y; Z) \leq 0\)。

同样，对于\(X \rightarrow Z \rightarrow Y\)，此时，条件化在\(Z\)上会使\(X\)和\(Y\)独立，因此\(I(X; Y | Z) \leq I(X; Y)\)，所以\(I(X; Y; Z) \geq 0\)。

5.5. 相互作用信息与熵的关系（MMI and Entropy）

MMI 还可以用熵来表达。我们知道：
\[I(X; Y) = H(X) + H(Y) - H(X, Y)\]

和
\[I(X; Y | Z) = H(X, Z) + H(Y, Z) - H(Z) - H(X, Y, Z)\]

因此，可以将\(I(X; Y; Z)\)重新写为：
\[I(X; Y; Z) = [H(X) + H(Y) + H(Z)] - [H(X, Y) + H(X, Z) + H(Y, Z)] + H(X, Y, Z)\]

跟集合比较相似。对于多个变量，MMI 可以推广为：
\[I(X_1, \dots, X_D) = - \sum_{T \subseteq \{1, \dots, D\}} (-1)^{|T|} H(T)\]

对于大小为 1, 2 和 3 的变量集，其展开为：
\[I_1 = H_1\]

\[I_{12} = H_1 + H_2 - H_{12}\]

\[I_{123} = H_1 + H_2 + H_3 - H_{12} - H_{13} - H_{23} + H_{123}\]

通过 Möbius 反演公式，可以得到熵和互信息的对偶关系：
\[H(S) = - \sum_{T \subseteq S} (-1)^{|T|} I(T)\]

使用链式规则，我们还可以得到 3 变量互信息的另一种形式：
\[I(X; Y; Z) = H(Z) - H(Z | X) - H(Z | Y) + H(Z | X, Y)\]

6. 互信息的变分界限

在直接计算互信息不可行的情况下，我们有一些估计其上界和下界的方法。

6.1 上界（Upper Bound）

假设联合分布\(p(x, y)\)难以直接计算，但我们可以从\(p(x)\)采样，并且能够计算条件分布\(p(y|x)\)。同时我们用\(q(y)\)来近似\(p(y)\)，此时互信息可以表示为：

\[I(x; y) = \mathbb{E}_{p(x,y)}\left[ \log \frac{p(y|x)}{q(y)} \right] - D_{KL}(p(y) \parallel q(y))\]

通过去掉KL散度项，我们得到一个互信息的上界：

\[I(x; y) \leq \mathbb{E}_{p(x)}\left[ D_{KL}(p(y|x) \parallel q(y)) \right]\]

该上界是当\(q(y) = p(y)\)时等号成立。

Not Found

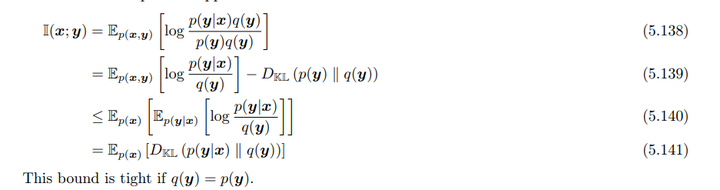
可以这么理解，互信息\(I(Y; X) = H(Y) - H(Y | X)\)，我们假设已知\(p(y|x)\)，因此可以很好地估计条件熵\(H(Y | X)\)。然而，关于边缘熵\(H(Y)\)，我们无法直接知道，所以我们用某个分布\(q(y)\)来对其进行上界估计。由于KL散度是非负的，因此我们的模型\(q(y)\)无法比真实的\(p(y)\)表现得更好，这意味着我们对\(H(Y)\)的估计总是偏大的，从而得到了互信息的估计的一个上界。

6.2 BA下界（BA Lower Bound）

假设我们可以计算\(p(x)\)，并且用\(q(x|y)\)来近似\(p(x|y)\)。那么互信息的变分下界为：

\[\begin{align*} I(x; y) &= \mathbb{E}_{p(x,y)} \left[ \log \frac{p(x|y)}{p(x)} \right] \\ &= \mathbb{E}_{p(x,y)} \left[ \log \frac{q(x|y)}{p(x)} \right] + \mathbb{E}_{p(y)} \left[ D_{\mathrm{KL}} (p(x|y) \parallel q(x|y)) \right] \\ &\geq \mathbb{E}_{p(x,y)} \left[ \log \frac{q(x|y)}{p(x)} \right] \\ &= \mathbb{E}_{p(x,y)} \left[ \log q(x|y) \right] + h(x) \end{align*}\]

这首先被Barber和Agakov提出，所以叫做BA下界。它的关键思想是使用容易计算的\(q(x|y)\)来近似\(p(x|y)\)，从而给出互信息的下界。

6.3 NWJ下界（NWJ Lower Bound）

NWJ下界是通过重新参数化\(q(x|y)\)得到的。我们可以设：

\[q(x|y) = \frac{p(x)e^{f(x,y)}}{Z(y)}\]

其中\(Z(y) = \mathbb{E}_{p(x)} \left[ e^{f(x,y)} \right]\)是归一化常数。这样我们可以得到新的变分下界：

\[\begin{align*} \mathbb{E}_{p(x,y)} \left[ \log \frac{p(x) e^{f(x,y)}}{p(x) Z(y)} \right] &= \mathbb{E}_{p(x,y)} \left[ f(x, y) \right] - \mathbb{E}_{p(y)} \left[ \log Z(y) \right] \\ &= \mathbb{E}_{p(x,y)} \left[ f(x, y) \right] - \mathbb{E}_{p(y)} \left[ \log \mathbb{E}_{p(x)} \left[ e^{f(x,y)} \right] \right] \\ &\equiv I_{\text{DV}}(X; Y) \end{align*}\]

这被叫做Donsker-Varadhan下界，为了进一步简化，可以用线性上界来逼近log函数

\[\log x \leq \frac{x}{a} + \log a - 1\]

最终得到NWJ下界的形式如下：

\[I(X; Y) \geq \mathbb{E}_{p(x,y)} \left[ f(x, y) \right] - e^{-1} \mathbb{E}_{p(y)} Z(y) \equiv I_{\text{NWJ}}(X; Y)\]

这个下界不需要归一化的分布（实践中我们使用蒙特卡洛采样估计就行），因此更易于计算。

6.4 InfoNCE下界（InfoNCE Lower Bound）

如果我们对DV下界进行多样本扩展，则可以得到InfoNCE下界。即对于每个样本\((x_i, y_i)\)，我们不只考虑它本身的联合分布，而是通过和其他样本进行对比来估计 mutual information。

假设我们有\(K\)对样本\(\{(x_i, y_i)\}_{i=1}^K\)​ ，其中\(x_i\)​ 和\(y_i\)来自联合分布\(p(x, y)\)，而\(y_j\)（对于\(i \neq j\)）来自边缘分布\(p(y)\)。为每一对\((x_i, y_i)\)，我们希望通过对比它与其他负样本（\((x_i, y_j)\)其中\(j \neq i\)）来计算 mutual information。最终其形式为：

\[I_{NCE} = \mathbb{E} \left[ \frac{1}{K} \sum_{i=1}^{K} \log \frac{e^{f(x_i, y_i)}}{\frac{1}{K} \sum_{j=1}^{K} e^{f(x_i, y_j)}} \right]\]

Not Found

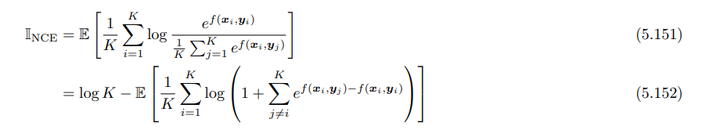
其中，\(f(x_i, y_i)\)是可学习的判别函数，表示\(x_i\)​ 和\(y_i\)​ 的关联性。这样便通过对比联合分布和边缘分布的采样来估计互信息。InfoNCE下界的一个缺点是，如果互信息较大，则需要较大的样本数\(K\)来得到准确的估计。

7. 相关网络（Relevance Networks）

相关网络是通过一组相关变量来构建的图网络。在这个网络中，如果两个变量\(X_i\)和\(X_j\)之间的互信息高于某个阈值，就会在它们之间添加一条边。这种方法可以应用于高斯分布情况下的变量，也可以扩展到离散随机变量。

在高斯分布情况下，两个变量之间的互信息可以通过它们的相关系数（Correlation Coefficient）计算，公式为：
\[I(X_i ; X_j ) = -\frac{1}{2} \log(1 - \rho_{ij}^2)\]

其中\(\rho_{ij}\)是\(X_i\)和\(X_j\)的相关系数。这种情况下的图称为协方差图（Covariance Graph）。

相关网络有一个主要问题：它通常会产生非常稠密的图。因为大多数变量在一定程度上都会与其他大多数变量相互依赖，即使我们对互信息进行了阈值处理，图中仍可能存在大量的边。例如：

假设\(X_1\)​ 直接影响\(X_2\)​，而\(X_2\)​ 又直接影响\(X_3\)​，此时它们组成了一个信号传导，\(X_1 \to X_2 \to X_3\)。在这种情况下，\(X_1\)和\(X_3\)​ 之间也会有非零的互信息，因此会有一条\(1-3\)的边，虽然它们之间没有直接的依赖关系。这样，图可能会在很多情况下甚至会变得完全连接。

四. 数据压缩（源编码）

数据压缩是信息理论的核心内容之一，也与概率机器学习密切相关。其基本思想是，我们对数据样本的不同种类建模，并且能够为出现频率最高的那些种类分配短的编码字，为出现频率较低的种类保留更长的编码。因此，数据压缩的能力需要发现数据中的潜在模式及其相对频率。

1. 无损压缩（Lossless Compression）

对于离散数据（如自然语言），总是可以以一种方式进行压缩，使我们能够唯一地恢复原始数据。这称为无损压缩。克劳德·香农证明了，从分布\(p\)中获取的数据所需的平均比特数至少为\(H(p)\)，这被称为源编码定理。

根据源编码定理，期望所需的比特数\(R\)满足以下不等式：

\[R \geq H(p)\]

其中\(H(p)\)是分布\(p\)的熵。使用非真实模型\(q\)进行压缩会导致多出的比特数，这正是 KL 散度的非负性所表明的。具体地，

\[H_{ce}(p, q) \geq H(p)\]

其中\(H_{ce}(p, q)\)是使用模型\(q\)对数据进行压缩时的交叉熵。

常见的无损编码技术包括 Huffman 编码、算术编码和非对称数字符号系统（Asymmetric Numeral Systems）等。

2. 有损压缩与率失真权衡（Lossy Compression and the Rate-Distortion Tradeoff）

对于实值信号（如图像和声音），首先需要对信号进行量化，得到一系列符号。然后可以使用无损编码方法来压缩这些离散符号序列。但是，在解压缩时会丢失一些信息，因此这种方法称为有损压缩。

有损压缩中存在一个重要的权衡关系，即压缩表示的大小（使用的符号数量）和由此产生的误差之间的权衡。我们使用了变分信息瓶颈（Variational Information Bottleneck）的术语来量化这种权衡，尤其是在无监督设置下。

• Distortion\(D\)的定义：

我们可以通过编码解码模型，假设有一个随机编码器\(e(z|x)\)、一个随机解码器\(d(x|z)\)和一个先验边际\(m(z)\),我们可以得到最终损失信息，即对失真的量化\(D\)如下：

\[D = - \int p(x) \int e(z|x) \log d(x|z) \, dz \, dx\]

如果解码器\(d(x|z)\)是一个确定性模型加上高斯噪声\(N(x | f_d(z), \sigma^2)\)，而编码器\(e(z|x)\)是确定性的\(\delta(z - f_e(x))\)，那么可以简化为：

\[D = \frac{1}{\sigma^2} \mathbb{E}_{p(x)} \| f_d(f_e(x)) - x \|_2^2\]

Not Found

• Rate\(R\)的定义：

\[\begin{align*} R &= \int p(x) \int e(z|x) \log \frac{e(z|x)}{m(z)} \, dz \, dx \\&=\mathbb{E}_{p(x)}[ H_{ce}​(e(z|x),m(z))−H(e(z|x))] \end{align*}\]

这里\(m(z)\)是先验边际分布。通过 KL 散度的平均来定义了这个率：

\[R = \mathbb{E}_{p(x)} \left[ D_{KL}(e(z|x) \| m(z)) \right]\]

这反映的是\(z\)后验分布与\(z\)的边缘分布的区别。如果我们使用\(m(z)\)来设计一个最优编码，那么\(R\)就是使用\(m(z)\)而不是实际的后验分布\(p(z) = \int dx \, p(x)e(z|x)\)进行编码时所需支付的额外比特数。

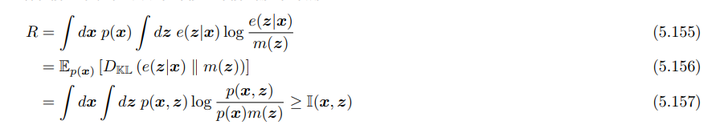* Rate-Distortion Bounds：

根据前面提到的互信息的变分界限（BA下界和上界），我们有以下不等式：

\[H - D \leq I(x; z) \leq R\]

其中\(H\)是（微分）熵。

• Rate-Distortion Curve：

可实现的\(R\)和\(D\)值形成的曲线称为率失真曲线（Rate-Distortion Curve）。这条曲线展示了在不同\(R\)和\(D\)条件下的可达值。例如，当\(D = 0\)时，我们可以完美地编码和解码数据，此时\(R \geq H\)，即所需的最小比特数为数据的熵。

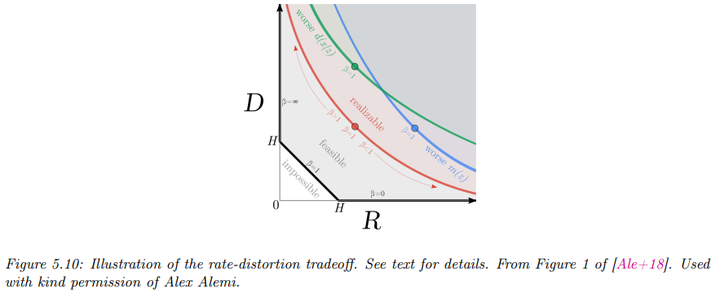水平的底线对应于零失真设置，即\(D = 0\)。这可以通过使用\(e(z|x) = \delta(z - x)\)的简单编码器来实现。

左侧的垂直线对应于零率设置，即潜变量与\(z\)独立。在这种情况下，解码器\(d(x|z)\)与\(z\)无关。即此时\(I(x; z)\)为0。这种模型能够达到的最小失真仍然是数据的熵，即\(D \geq H\)。

使用互信息的变分界限可以更精确地刻画率和失真之间的权衡关系。实际上，我们无法在对角线上达到点，因为这要求在不等式中均取等号，即需要我们的模型\(e(z|x)\)和\(d(x|z)\)是完美的，这被称为“非参数限制”。在有限数据设置中，我们总会产生额外的误差，因此 RD 曲线会向上偏移。

我们可以通过最小化以下目标函数\(J\)来生成不同的解决方案：

\[J = D + \beta R\]

其中：\(D\)是失真（distortion），表示编码与解码之间的误差。\(R\)是rate，表示编码所需的比特数。\(\beta\)是一个权重超参数，用于调节失真和rate之间的平衡。

目标函数可以展开为：

\[J = \int dx \, p(x) \int dz \, e(z|x) \left( -\log d(x|z) + \beta \log \frac{e(z|x)}{m(z)} \right)\]

当\(\beta = 1\)时，公式与变分自编码器（VAE）目标一致:

\[\mathcal{L} = - (D + R) = E_{p(x)} \left[ E_{e(z|x)}[\log d(x|z)] - E_{e(z|x)} \left[ \log \frac{e(z|x)}{m(z)} \right] \right]\]

3. 信息瓶颈（The information bottleneck）

3.1 原版信息瓶颈（Vanilla IB）

信息瓶颈（The information bottleneck）的目标是通过引入一个中间表示\(z\)，在输入\(x\)和输出\(y\)之间传递信息。我们说\(z\)是\(x\)的表示，可以用条件分布\(p(z|x)\)来描述。

• 充分性：表示\(z\)对于任务\(y\)是充分的，条件为\(y \perp x | z\)，或等价于\(I(z; y) = I(x; y)\)，即\(H(y|z) = H(y|x)\)。
• 最小充分统计量：如果\(z\)是充分的，并且没有其他\(z\)具有更小的\(I(z; x)\)值，则称其为最小充分统计量。

目标是找到一个表示\(z\)，使得\(I(z; y)\)最大化，同时\(I(z; x)\)最小化，即优化以下目标：

\[\min_\beta I(z; x) - I(z; y)\]

其中\(\beta \geq 0\)，优化的分布为\(p(z|x)\)和\(p(y|z)\)。

在信息瓶颈原理中，我们假设\(Z\)是\(X\)的一个函数，但与\(Y\)独立，形成图模型\(Z \leftarrow X \rightarrow Y\)。这对应于以下联合分布：

\[p(x, y, z) = p(z|x) p(y|x) p(x)\]

这表明\(Z\)可以捕捉\(X\)的任何信息，但不能包含仅与\(Y\)相关的信息。优化的表示只捕获对\(Y\)有用的关于\(X\)的信息，并且\(Z\)应该最小化对\(X\)的信息，以避免“浪费容量”。

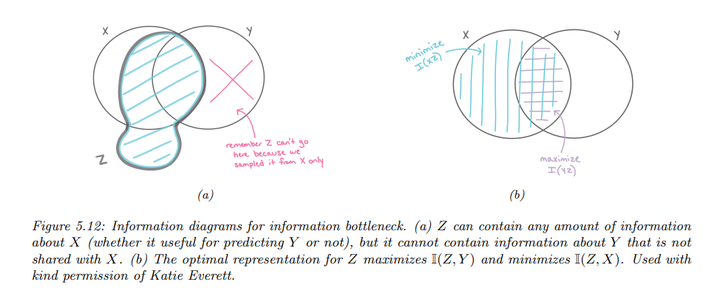如果所有随机变量都是离散的，并且\(z = e(x)\)是\(x\)的确定性函数，则可以使用传统算法来最小化信息瓶颈目标。如果所有变量都是联合高斯的，目标也可以通过解析求解。但一般情况下，精确求解该问题是不可行的。

3.2. 变分信息瓶颈（Variational IB）

根据 KL 散度的非负性，我们介绍到对于任意分布\(q\)，有：

\[\int dx p(x) \log p(x) \geq \int dx p(x) \log q(x)\]

首先定义符号：

\(e(z|x) = p(z|x)\)：编码器 \(b(z|y) \approx p(z|y)\)：反向编码器 \(d(y|z) \approx p(y|z)\)：分类器（解码器） \(m(z) \approx p(z)\)：边际分布

推导\(I(z; y)\)：

\[\begin{align*} I(z; y) &= \int \! dydz \, p(y, z) \log \frac{p(y, z)}{p(y)p(z)} \\ &= \int \! dydz \, p(y, z) \log p(y|z) - \int \! dydz \, p(y, z) \log p(y) \\ &= \int \! dydz \, p(z)p(y|z) \log p(y|z) - \text{const} \\ &\geq \int \! dydz \, p(y, z) \log d(y|z) \\ &= \langle \log d(y|z) \rangle \end{align*}\]

这里利用了\(H(p(y))\)是与表示无关的常量。符号\(\langle \cdot \rangle\)表示对联合分布\(p(x, y, z)\)相关项的期望值

随后，通过从\(p(y, z) = \int dx \, p(x)p(y|x)p(z|x)\)采样，近似求期望值。

同样地，我们可以推导\(I(z; x)\)的上界：

\[\begin{align*} I(z; x) &= \int dzdx \, p(x, z) \log \frac{p(z, x)}{p(x)p(z)} \\ &= \int dzdx \, p(x, z) \log p(z|x) - \int dz \, p(z) \log p(z) \\ &\leq \int dzdx \, p(x, z) \log p(z|x) - \int dz \, p(z) \log m(z) \\ &= \int dzdx \, p(x, z) \log \frac{e(z|x)}{m(z)} \\ &= \langle \log e(z|x) \rangle - \langle \log m(z) \rangle \end{align*}\]

通过近似从\(p(x, z) = p(x)p(z|x)\)采样，我们可以计算期望。

综合以上结果，我们得到信息瓶颈目标函数的上界：

\[\beta I(x; z) - I(z; y) \leq \beta (\langle \log e(z|x) \rangle - \langle \log m(z) \rangle) - \langle \log d(y|z) \rangle\]

因此，VIB 的目标函数可以表示为：

\[\begin{align*} L_{VIB} &= \beta \, \mathbb{E}_{p_D(x)e(z|x)} \left[ \log e(z|x) - \log m(z) \right] - \mathbb{E}_{p_D(x)e(z|x)d(y|z)} \left[ \log d(y|z) \right] \\ &= -\mathbb{E}_{p_D(x)e(z|x)d(y|z)} \left[ \log d(y|z) \right] + \beta \, \mathbb{E}_{p_D(x)} \left[ D_{KL} \left( e(z|x) \parallel m(z) \right) \right] \end{align*}\]

这个目标函数可以通过随机梯度下降（SGD）对编码器、解码器和边际分布的参数进行最小化。我们假设这些分布是可重参数化的。对于编码器\(e(z|x)\)，通常使用条件高斯分布；对于解码器\(d(y|z)\)，通常使用 softmax 分类器。对于边际分布\(m(z)\)，由于其需要近似聚合的后验分布\(p(z)\)，通常使用灵活的模型，比如高斯混合模型。

Not Found

3.3 条件熵瓶颈（Conditional Entropy Bottleneck）

信息瓶颈的基本目标是最大化互信息\(I(Z; Y)\)的同时最小化互信息\(I(Z; X)\)。可以表示为：

\[\min I(X; Z) - \lambda I(Y; Z) \quad (\lambda \geq 0)\]

然而，从信息图的视角来看，\(I(Z; X)\)中包含了一些与\(Y\)相关的信息。一个合理的替代目标是最小化残余互信息\(I(X; Z | Y)\)：

\[\min I(X; Z | Y) - \lambda' I(Y; Z) \quad (\lambda' \geq 0)\]

这就是条件熵瓶颈（CEB）。

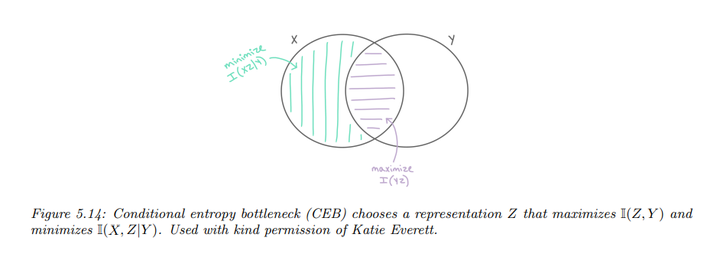我们假设\(p(Z | X, Y) = p(Z | X)\)，则根据条件互信息的定义：

\[I(X; Z | Y) = I(X; Z) - I(Y; Z)\]

因此，CEB 可以看作是标准的 IB 方法，当\(\lambda' = \lambda + 1\)时，两者等价。

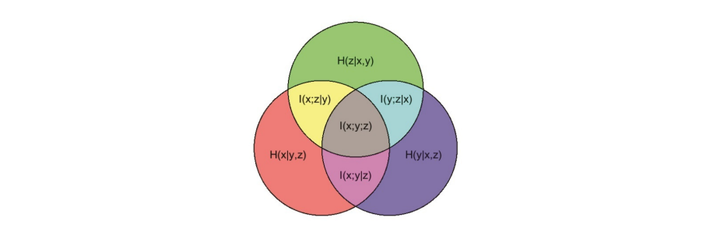相较于\(I(X; Z)\)，\(I(X; Z | Y)\)的上界更容易确定，因为我们在\(Y\)的条件下进行计算。利用\(p(Z | X, Y) = p(Z | X)\)的性质，可以得出：

\[\begin{align*} I(X; Z | Y) &= I(X; Z) - I(Y; Z) \\ &= H(Z) - H(Z | X) - [H(Z) - H(Z | Y)] \\ &= - H(Z | X) + H(Z | Y) \\ &= \int dz dx \, p(x, z) \log p(z | x) \\ &\leq \int dz dx \, p(x, z) \log e(z | x) - \int dz dy \, p(z, y) \log b(z | y) \\ &= \langle \log e(z | x) \rangle - \langle \log b(z | y) \rangle \end{align*}\]

结合以上推导，我们得到最终的条件熵瓶颈目标：

\[\min \beta \left( \langle \log e(z|x) \rangle - \langle \log b(z|y) \rangle \right) - \langle \log d(y|z) \rangle\]

学习条件反向编码器\(b(z|y)\)通常比学习无条件边际\(m(z)\)更容易。此外，我们知道，当\(I(X; Z | Y) = I(X; Z) - I(Y; Z) = 0\)时，此时的\(\beta\)值对应于一个最优的表示。相比之下，在使用信息瓶颈（IB）时，如何衡量与最优性的距离并不明确。

五、算法信息理论

考虑一个从均匀伯努利分布独立生成的长度为\(n\)的比特序列。该分布每个元素的最大熵为\(H_2(0.5) = 1\)，因此长度为\(n\)的序列的编码长度为\(- \log_2 p(D|\theta) = - \sum_{i=1}^{n} \log_2 \text{Ber}(x_i | \theta = 0.5) = n\)。然而，从直观上来看，这样的序列并没有包含太多信息。

可见统的信息理论主要基于某个随机分布的性质，这种分布被假设为生成我们观察到的数据。然而，这种理论并没有很好地反映出人们对“信息”的直观理解，而算法信息理论提出了一种不同的方法来量化一个序列的信息量。

1. Kolmogorov复杂性

Kolmogorov复杂性是算法信息理论的核心概念，定义为生成特定比特字符串\(x = x_{1:n}\)的最短程序的长度。这一程序被输入到一个通用图灵机\(U\)中，以生成字符串\(x\)。公式定义为：

\[K(x) = \min_{p \in B^*} [\ell(p) : U(p) = x]\]

\(B^*\)是任意长度比特字符串的集合。 \(\ell(p)\)是程序\(p\)的长度。

Kolmogorov复杂性具有一些类似于Shannon熵的性质。我们可以忽略常数项，得到以下不等式：

\[K(x|y) \leq K(x) \leq K(x, y)\]

这些不等式的解释如下：

\(K(x∣y)\)：在已知\(y\)的情况下，生成\(x\)的最短程序长度。 \(K(x)\)：生成\(x\)的最短程序长度。 *\(K(x, y)\)：生成\(x\)和\(y\)的最短程序长度。

这些不等式表明，已知条件信息\(y\)会减少生成\(x\)所需的信息量。

尽管Kolmogorov复杂性是一个理论上重要的概念，但它是不可计算的。为了解决这个问题，引入了Levin复杂性：

\[L(x) = \min_{p \in B^*} [\ell(p) + \log(\text{time}(p)) : U(p) = x]\]

*\(\text{time}(p)\)是程序\(p\)的运行时间。

Levin复杂性可以通过“Levin搜索”或“通用搜索”来计算，即以时间片的方式运行所有程序，直到第一个程序停止。这种方法的时间复杂度为：

\[\text{time}(LS(x)) = 2^{L(x)}\]

虽然Levin复杂性是可计算的，但计算效率仍然较低。为此，可以通过参数化的近似来得到Kolmogorov复杂性的上界。例如，假设\(q\)是某个比特字符串的分布，可以证明：

\[K(x) \leq -\log q(x) + K(q)\]

如果\(q\)是一个参数化模型，可以通过\(q\)参数的编码长度来近似\(K(q)\)。

Kolmogorov复杂性还可以用于定义序列的随机性定义，而无需使用随机变量或通信信道的概念。我们定义一个字符串\(x\)是可压缩的，当其最短描述长度小于字符串本身的长度：

\[K(x) < \ell(x) = n\]

否则，称字符串为算法随机的。这种随机性定义称为Martin-Löf随机性。

例如：

• 字符串\(x = (10101010 \ldots)\)是可压缩的，因为它是模式“10”的重复。
• 字符串\(x = (11001001 \ldots)\)也是可压缩的，但不如前者明显，因为它是\(\pi^2\)的二进制扩展。
• 字符串\(x = (10110110 \ldots)\)被认为是“真正随机的”，因为它来源于量子波动。

基于序列的信息理论为著名的Lempel-Ziv无损数据压缩方案奠定了基础，这形成了zip编码的基础。利用Kolmogorov复杂性，我们可以定义一种普遍相似性度量：

\[d(x, y) = \frac{\max[K(x|y), K(y|x)]}{\max[K(x), K(y)]}\]

其中，诸如\(K(x)\)的项可以通过某种通用压缩器（如LZ）的编码成本进行近似。这导致了规范化压缩距离（NCD）的出现。

2. Solomonoff归纳

在Solomonoff归纳中，我们关注的是预测问题。假设我们观察到了一系列数据\(x_{1:t}\)​，这些数据来自某个未知的分布\(\mu(x_{1:t})\)。我们的目标是通过某个模型\(\nu\)来近似这个分布，以便预测未来的值，即\(\nu(x_{t+1}|x_{1:t})\)。这被称为归纳问题。

我们假设\(\nu\)属于模型集合\(M\)，其中\(M\)是一个可数模型（分布）的集合。对于每个模型\(\nu\)，我们有一个先验概率\(w_\nu\)​。在Solomonoff归纳中，模型集合\(M\)被假设为所有可计算函数的集合，先验定义为：

\[w_\nu = 2^{-K(\nu)}\]

这个“通用先验”能够建模任何可计算的分布\(\mu\)。这里的权重选择是基于奥卡姆剃刀原理，即我们应该偏好那些最简单的能够解释数据的模型。

给定这个先验，我们可以使用以下贝叶斯混合模型计算序列的先验预测分布：

\[\xi(x_{1:t}) = \sum_{\nu \in M} w_\nu \nu(x_{1:t})\]

从这个先验预测分布出发，我们可以在时间步骤\(t\)计算后验预测分布：

\[\begin{align*} \xi(x_t|x_{<t}) &= \frac{\xi(x_{1:t})}{\xi(x_{<t})} \\ &= \frac{\sum_{\nu \in M} w_\nu \nu(x_{1:t})}{\xi(x_{<t})} \\ &= \sum_{\nu \in M} w_\nu \frac{\nu(x_{1:t})}{\xi(x_{<t})} \\ &= \sum_{\nu \in M} w_\nu \frac{\nu(x_{<t})}{\xi(x_{<t})} \nu(x_t|x_{<t}) \\ &= \sum_{\nu \in M} w(\nu|x_{<t}) \nu(x_t|x_{<t}) \end{align*}\]

在最后一步中，我们利用了后验权重的性质：

\[w(\nu|x_{1:t}) = \frac{p(\nu|x_{1:t})}{p(x_{1:t})} = \frac{w_\nu \nu(x_{1:t})}{\xi(x_{1:t})}\]

考虑在每个时间步骤\(t\)上，比较这种预测分布与真实分布的准确性。我们用平方误差来表示：

\[s_t(x_{<t}) = \sum_{x_t \in X} (\mu(x_t|x_{<t}) - \xi(x_t|x_{<t}))^2\]

考虑到直到时间\(n\)的总期望误差：

\[S_n = \sum_{t=1}^{n} \sum_{x_{<t} \in X} \mu(x_{<t}) s_t(x_{<t})\]

Solomonoff证明了这个预测器的总误差在极限情况下的一个重要界限：

\[S_\infty \leq \ln(w^{-1}_\mu) = K(\mu) \ln 2\]

这一结果表明，总误差被生成数据的环境复杂性所界定，简单的环境易于学习，最优预测器的预测迅速接近真实值。

我们还可以考虑一种假设，即数据是由某个未知的确定性程序\(p\)生成的，满足\(U(p) = x^*\)，其中\(x^*\)是观察到的前缀\(x = x_{1:t}\)的无限扩展。假设程序的先验定义为：

\[\Pr(p) = 2^{-\ell(p)}\]

那么序列的先验预测分布为：

\[M(x) = \sum_{p: U(p) = x^*} 2^{-\ell(p)}\]

可以证明\(M(x) = \xi(x)\)

由此，我们可以计算后验预测分布\(M(x_t|x_{<t}) = \frac{M(x_{1:t})}{M(x_{<t})}\)。

由于Solomonoff归纳依赖于Kolmogorov复杂性来定义其先验，因此它是不可计算的。然而，可以通过各种方式对这一方案进行近似。例如，可以使用元学习（meta learning）来训练通用序列预测器，如Transformer或LSTM，使得这些模型能够近似一个通用预测器。

3. AXI和通用AGI

最后讲了AIXI，是一个对Solomonoff归纳法的扩展，书中说的比较简略：

Not Found