[Probabilistic Machine Learning]: Fundamentals-Optimization

优化问题通常可以表示为：

\[\theta^* \in \arg\min_{\theta \in \Theta} L(\theta)\]

其中，\(\theta^*\)是优化得到的参数，\(\Theta\)是参数空间，可以是任意维度的实数集合，而\(L(\theta)\)是目标函数或损失函数，它衡量了参数与某种目标之间的距离。

凸优化问题的局部最优解即是全局最优解，而非凸问题可能有多个局部最优解。

一、自动微分（Automatic Differentiation）

自动微分（AD）是计算复杂函数的导数的有效方法，尤其是在深度学习和优化中具有重要应用。AD与数值微分和符号微分不同，它通过跟踪计算图来有效计算导数。

1. 函数微分的基础知识

在介绍自动微分之前，首先需要了解导数的数学基础。

• 符号表示

给定函数\(f : \mathbb{R}^2 \rightarrow \mathbb{R}\)，我们可以写其关于第一个参数的偏导数为\(\frac{\partial f}{\partial x_1}\bigg|_{x=a}\)或者\(\frac{\partial}{\partial a_1} f(a_1, a_2)\)

这种命名变量表示法在函数嵌套较多时会变得复杂，因此可以考虑采用函数操作符的表示法。

• 线性和多线性函数：

定义线性函数\(F : \mathbb{R}^n \overset{\ell}{\rightarrow} \mathbb{R}^m\)。每个线性映射对应一个矩阵，其列由\(F[e_1], \ldots, F[e_n]\)组成（具体线性代数课已经证明并详细学习了）。

多线性映射定义为：

\[T : \mathbb{R}^n \times \cdots \times \mathbb{R}^n \rightarrow \mathbb{R}^m \ \]

它对应于\(\mathbb{R}^{m \times n \times \cdots \times n}\)中的一个张量。用\(T[x_1, \ldots, x_k] \in \mathbb{R}^m\)表示这样的\(k\)-线性映射对向量\(x_1, \ldots, x_k \in \mathbb{R}^n\)的作用。

• 导数算子

对可微分函数\(f : U \rightarrow \mathbb{R}^m\)，其导数可以表示为：

\[\partial f : U \rightarrow (\mathbb{R}^n \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

或者等价地：

\[\partial f : U \rightarrow \mathbb{R}^{m \times n}\]

雅可比矩阵表示为所有偏导数组成的矩阵，给定\(x \in U\)，可以表示为：

\[J(x) = \partial f(x)\]

雅可比-向量积 (JVP)定义为：

\[(x, v) \mapsto \partial f(x)[v]\]

它表示在点\(x\)处，输入扰动\(v\)对输出的影响。

向量-雅可比积 (VJP)定义为：

\[(x, u) \mapsto \partial f(x)^T[u]\]

它表示在点\(x\)处，输出扰动\(u\)对应输入的变化。

• 高阶导数

如果函数\(f\)在其域\(U\)内任意可微，则其二阶导数写作：

\[\partial^2 f : U \rightarrow (\mathbb{R}^n \overset{\ell}{\rightarrow} \mathbb{R}^n \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

对于任意高阶导数，可以表示为：

\[\partial^k f : U \rightarrow (\mathbb{R}^n \overset{\ell}{\rightarrow} \cdots \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

\(\partial^2 f\)在\(m=1\)时对应于海森矩阵。

泰勒级数近似：

\[f(x + v) \approx f(x) + \partial f(x)[v] + \frac{1}{2!} \partial^2 f(x)[v, v] + \cdots + \frac{1}{k!} \partial^k f(x)[v, \ldots, v]\]

• 多个输入

考虑一个两个参数的函数：

\[g : U \times V \rightarrow \mathbb{R}^m\]

其中\(U \subset \mathbb{R}^{n_1}​\)和\(V \subset \mathbb{R}^{n_2}\)​。

导数函数可以分别表示为：

\[\partial_1 g : \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow (\mathbb{R}^{n_1} \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

\[\partial_2 g : \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow (\mathbb{R}^{n_2} \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

总导数表示为：

\[\partial g : \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow (\mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \overset{\ell}{\rightarrow} \mathbb{R}^m)\]

对于点\((x, y) \in U \times V\)和扰动\(\dot{x} \in \mathbb{R}^{n_1}，\dot{y} \in \mathbb{R}^{n_2}\)​，有：

\[\partial g(x, y)[\dot{x}, \dot{y}] = \partial_1 g(x, y)[\dot{x}] + \partial_2 g(x, y)[\dot{y}]\]

或者，从矩阵的角度来看：

\[\partial g(x, y) = \begin{pmatrix} \partial_1 g(x, y) & \partial_2 g(x, y) \end{pmatrix}\]

• 组合和分支

当我们有复合函数\(f = g \circ h\)时，链式法则表明：

\[\partial f(x) = \partial g(h(x)) \circ \partial h(x)\]

当存在多个输入时，比如：

\[f(x) = g(a(x), b(x))\]

我们可以使用链式法则来计算：

\[\begin{align*} \partial f(x) &= \partial g(h(x)) \circ \partial h(x) \\ &= \partial_1 g(a(x), b(x)) \circ \partial a(x) + \partial_2 g(a(x), b(x)) \circ \partial b(x) \end{align*}\]

2. 链法则到计算图

自动微分的目标是计算任意输入函数的导数。对于给定的函数\(f: U \subset \mathbb{R}^n \to \mathbb{R}^m\)和线性化点\(x \in U\)，AD 可以计算：

• 输入扰动\(v \in \mathbb{R}^n\)的 JVP：\(\partial f(x)[v]\)
• 输出扰动\(u \in \mathbb{R}^m\)的 VJP：\(\partial f(x)^T[u]\)

决定使用哪些函数作为输入，以及如何表示这些函数，是AD设置中最重要的方面之一。

2.1 链式组合和链式法则

这里考虑的函数是基本操作的链式组合。链式组合的导数按照链式法则分解，从而提供了一种便利的函数表示形式。例如，考虑由三个操作依次组成的函数：
\(f = c \circ b \circ a\)

根据链式法则，其导数为：
\[\partial f(x) = \partial c(b(a(x))) \circ \partial b(a(x)) \circ \partial a(x)\]

针对输入扰动\(v \in \mathbb{R}^n\)的 JVP 可以表示为：
\[\partial f(x)[v] = \partial c(b(a(x))) [\partial b(a(x)) [\partial a(x)[v]]]\]

这个表达式的括号突出了从右到左的评估顺序，这对应于前向模式自动微分。为了计算这个 JVP，我们需要首先计算原始链的前缀：
\[x, \quad a(x), \quad b(a(x))\]

以及相应的偏导数：
\[\partial a(x), \quad \partial b(a(x)), \quad \partial c(b(a(x)))\]

所以，具体的算法如下：

对于输出扰动\(u\in \mathbb{R}^m\)，VJP 的表达式为：
\[\partial f(x)^T[u] = \partial a(x)^T \partial b(a(x))^T \partial c(b(a(x)))^T[u]\]

这里对应于反向模式自动微分。

为了进行 VJP，我们可以首先计算原始链的前缀

\(x、a(x)、 b(a(x))\)

然后反向读取它们，具体为：
\[\partial c(b(a(x)))^T, \quad \partial b(a(x))^T, \quad \partial a(x)^T\]

反向模式自动微分在输出为标量时（如深度学习中的损失函数）比前向模式更快。然而，反向模式在向后遍历之前存储所有链的前缀，因此它消耗的内存比前向模式多。

在某些特殊情况下（如每个链操作都是可逆的），可以通过一些方法减少内存需求。还可以通过丢弃某些前缀并在需要时重新计算来在内存与计算之间进行权衡。

2.2 从链到计算图

当原语可以接受多个输入时，我们可以自然地将链扩展为电路（circuits）——即基于原语操作的有向无环图（DAG），也称为计算图。电路会有若干个输入节点，表示函数的参数；也有若干个原语节点，每个节点都标记为某种原语操作。输入节点没有入边（即没有其他节点指向它们），并且每个节点恰好有一条出边，同时图中只有一个汇点（输出节点）。电路的整体功能是从输入节点到汇点的操作组合，每个操作的输出作为其他操作的输入。

对于链的自动微分之所以有效，是因为导数沿链可以分解，这得益于著名的链式法则。当我们从链转向有向无环图时，我们是否需要某种“图法则”来沿电路结构分解计算呢？电路引入了两个新特性：入度（fan-in）和出度（fan-out）。

• 入度（fan-in）：当一个原语操作接受多个参数时，会出现入度。在第1小节中，我们知道多个参数可以视为一个参数，因此链式法则适用。
• 出度（fan-out）：出度在反向模式微分中需要稍微更多的关注。

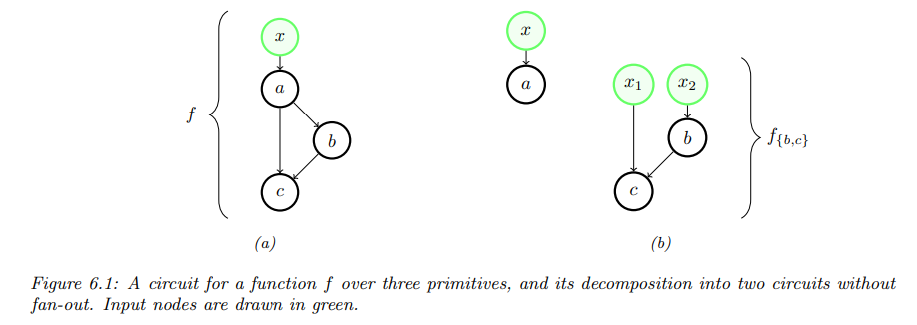
示例说明

考虑上图的电路。操作\(a\)在拓扑上位于\(b\)和\(c\)之前，并且有一条出边指向它们。我们可以将\(a\)从\(\{b, c\}\)中切割出来，生成两个新电路，如上图(b)所示。第一个电路对应于\(a\)，第二个电路的计算为：

\[f_{\{b,c\}}(x_1, x_2) = c(x_1, b(x_2))\]

我们可以通过一个名为\(dup\)的函数来恢复完整的函数\(f\)：

\[dup(x) = (x, x) \equiv \begin{pmatrix} I \\ I \end{pmatrix} x\]

因此，函数\(f\)可以写为链式组合：

\[f = f_{\{b,c\}} \circ dup \circ a\]

电路\(f_{\{b,c\}}\)不包含出度，其导数与\(b\)、\(c\)及其导数的关系，都是通过链式法则实现的。同时，根据链式法则：

\[\begin{align*} \partial f(x) &= \partial f_{\{b,c\}}(dup(a(x))) \circ \partial dup(a(x)) \circ \partial a(x) \\&= \partial f_{\{b,c\}}(a(x), a(x)) \circ \begin{pmatrix} I \\ I \end{pmatrix} \circ \partial a(x) \end{align*}\]

以上表达式表明，可以通过从右到左的评估来计算\(f\)的 JVP。这类似于链情况中建议的 JVP 计算，但中间有一个复制的操作\(\begin{pmatrix} I \\ I \end{pmatrix}\)，即\(dup\)的雅可比矩阵。

对\(f\)在\(x\)处的导数进行转置：

\[\partial f(x)^T = \partial a(x)^T \circ (I \ \ I) \circ \partial f_{\{b,c\}}(a(x), a(x))^T\]

考虑从右到左的评估，这同样类似于链情况中建议的 VJP 计算，但中间有一个求和操作\((I\ \ I)\)，即\(dup\)的转置雅可比矩阵。

二、 随机优化

这节我们主要考虑形式为\(L(\theta) = \mathbb{E}_{q_\theta(z)} \left[ \tilde{L}(\theta, z) \right]\)的随机目标优化，其中\(\theta\)是我们要优化的参数，\(z\)是随机变量，例如外部噪声，采样数据或者隐变量等。

1. 随机梯度下降 (SGD)

假设我们能够计算目标函数梯度的无偏估计\(g_t\)​ ，即：

\[\mathbb{E}[g_t] = \nabla_\theta L(\theta) |_{\theta_t}\]

则我们可以在梯度下降过程中使用它：

\[\theta_{t+1} = \theta_t - \eta_t g_t\]

其中\(\eta_t\)是学习率或步长。这被称为随机梯度下降（SGD）。SGD 收敛速度可能较慢，因为它依赖于梯度的随机估计。目前已经提出多种方法以减少每一步生成的参数估计的方差，从而加速收敛。

在使用 SGD 时，我们需要选择学习率来更好地收敛。我们可以使用学习率调度，而不是选择单一的常数学习率，逐步调整步长。理论上，SGD 收敛的充分条件是学习率调度满足 Robbins-Monro 条件：

\[\eta_t \to 0, \quad \sum_{t=1}^\infty \eta_t^2 < \infty, \quad \sum_{t=1}^\infty \eta_t = \infty\]

一些常见的学习率调度示例如下：

• 分段常数：\(\eta_t = \eta_i \quad \text{if } t_i \leq t \leq t_{i+1}\)
• 指数衰减：\(\eta_t = \eta_0 e^{-\lambda t}\)
• 多项式衰减：\(\eta_t = \eta_0 (\beta t + 1)^{-\alpha}\)

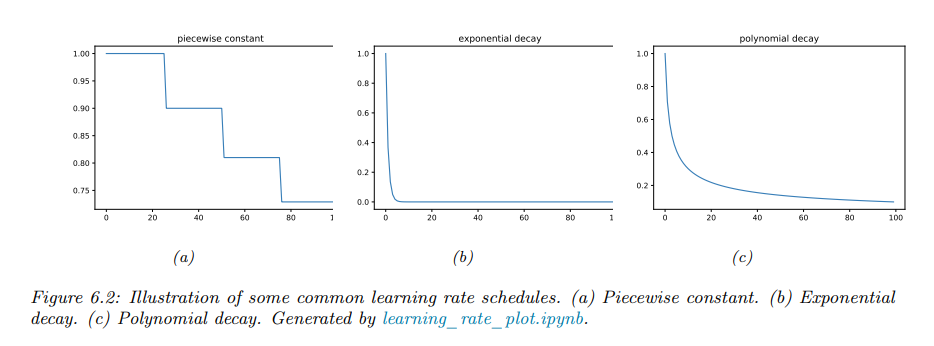
在许多情况下，梯度的大小在各个维度之间可能差异很大，导致损失面在某些方向上陡峭而在其他方向上较为平坦，类似于一个山谷的底部。在这种情况下，可以用条件矩阵\(C_t\)来缩放梯度向量，从而实现更快的收敛：

\[\theta_{t+1} = \theta_t - \eta_t C_t g_t\]

这被称为预条件 SGD。

2. SGD 用于优化有限和目标

在最简单的情况下，计算期望的分布\(q_\theta(z)\)不依赖于正在优化的参数\(\theta\)（即噪声或者数据与参数无关）。在这种情况下，我们可以将梯度推入期望算子内部，然后通过 Monte Carlo 采样来近似梯度：

\[\begin{align*} \nabla_\theta L(\theta) &= \nabla_\theta \mathbb{E}_{q(z)} \left[ \tilde{L}(\theta, z) \right] \\ &= \mathbb{E}_{q(z)} \left[ \nabla_\theta \tilde{L}(\theta, z) \right] \\ &\approx \frac{1}{S} \sum_{s=1}^{S} \nabla_\theta \tilde{L}(\theta, z_s) \end{align*}\]

其中\(S\)是采样数量。例如，考虑经验风险最小化（ERM）的问题，要求最小化：

\[L(\theta) = \frac{1}{N} \sum_{n=1}^{N} \tilde{L}(\theta, z_n) = \frac{1}{N} \sum_{n=1}^{N} \ell(y_n, f(x_n; \theta))\]

其中\(z_n = (x_n, y_n)\)是第\(n\)个标记示例，\(f\)是预测函数。这种目标称为有限和目标。我们可以将其写为关于经验分布\(p_D(x, y)\)的期望损失：

\[L(\theta) = \mathbb{E}_{p_D(z)} \left[ \tilde{L}(\theta, z) \right]\]

由于期望依赖于数据，而不是参数，我们可以通过在每次迭代中使用来自完整数据集\(D\)的\(B = |B|\)个数据点的小批量来近似梯度：

\[g_t = \nabla L(\theta_t) = \frac{1}{B} \sum_{n \in B} \nabla \ell(y_n, f(x_n; \theta))\]

这些带噪声的梯度可以传递给 SGD。当数据集很大时，这种方法比全批梯度下降快得多，因为它不需要在更新模型之前评估所有示例的损失 。

3. SGD 用于优化分布的参数

现在假设随机性依赖于我们正在优化的参数。例如，在强化学习中，\(z\)可能是从随机策略\(q_\theta\)​ 中采样的动作，或者在随机变分推理中，\(z\)可能是从推理网络\(q_\theta\)​ 中采样的潜变量。

在这种情况下，梯度为：

\[\begin{align*} \nabla_\theta \mathbb{E}_{q_\theta(z)}\left[\tilde{L}(\theta, z)\right] &= \nabla_\theta \int \tilde{L}(\theta, z) q_\theta(z) \, dz \\ &= \int \nabla_\theta \tilde{L}(\theta, z) q_\theta(z) \, dz \\ &= \int \left[\nabla_\theta \tilde{L}(\theta, z)\right] q_\theta(z) \, dz + \int \tilde{L}(\theta, z) \left[\nabla_\theta q_\theta(z)\right] \, dz \end{align*}\]

第一个项可以通过 Monte Carlo 采样近似：

\[\int \left[ \nabla_\theta \tilde{L}(\theta, z) \right] q_\theta(z) dz \approx \frac{1}{S} \sum_{s=1}^{S} \nabla_\theta \tilde{L}(\theta, z_s)\]

其中\(z_s \sim q_\theta\)​。

现在考虑第二项，注意，如果\(\tilde{L}\)与\(\theta\)无关，则此项消失，但如果相关，则该项涉及分布本身的梯度：

\[I \equiv \int \tilde{L}(\theta, z) [\nabla_\theta q_\theta(z)] dz\]

我们不能再使用简单的 Monte Carlo 采样来近似这个积分。然而，还有其他各种方法可以近似这个积分。将在后面简要描述两种主要方法。

4 分数函数估计器（REINFORCE）

分数函数是对数概率分布的梯度，其表达式为：
\[\nabla_\theta q_\theta(z) = q_\theta(z) \nabla_\theta \log q_\theta(z)\]

利用上述分数函数定义，可以将积分式的目标函数梯度表达式重新写为：
\[\begin{align*} I &= \int \tilde{L}(\theta, z) [q_\theta(z) \nabla_\theta \log q_\theta(z)] \, dz \\ &= \mathbb{E}_{q_\theta(z)}\left[\tilde{L}(\theta, z) \nabla_\theta \log q_\theta(z)\right] \end{align*}\]

这里，\(I\)表示我们要计算的梯度期望。

通过蒙特卡洛方法，可以对上述积分进行近似：
\[I \approx \frac{1}{S} \sum_{s=1}^{S} \tilde{L}(\theta, z_s) \nabla_\theta \log q_\theta(z_s)\]

其中\(z_s \sim q_\theta\)​。

为了降低分数函数估计的方差，可以使用控制变量的方法，将\(\tilde{L}(\theta, z)\)替换为：
\[\hat{\tilde{L}}(\theta, z) = \tilde{L}(\theta, z) - c \left(b(\theta, z) - \mathbb{E}[b(\theta, z)]\right)\]

这里，\(b(\theta, z)\)是与\(\tilde{L}(\theta, z)\)相关的基线函数，\(c > 0\)是一个系数。使用此新的估计\(\hat{\tilde{L}}\)计算的梯度估计仍然是无偏的，但具有较低的方差。

当\(q_\theta(z)\)是离散分布时，目标函数为：
\[L(\theta) = \sum_{z} \tilde{L}(\theta, z) q_\theta(z)\]

梯度计算为：
\[\nabla_\theta L(\theta) = \sum_{z} \tilde{L}(\theta, z) \nabla_\theta q_\theta(z)\]

如果\(z\)可以取指数级多的值，直接计算可能不可行。可以将和分为两部分：一部分\(S_1\)​ 是高概率值的小集合，另一部分\(S_2\)​ 是所有其他值的大集合。梯度的计算可以表达为：
\[\nabla_\theta L(\theta) = \sum_{z \in S_1} \tilde{L}(\theta, z) \nabla_\theta q_\theta(z) + \mathbb{E}_{q_\theta(z|z \in S_2)}\left[\tilde{L}(\theta, z) \nabla_\theta \log q_\theta(z)\right]\]

对于第二项的计算，可以使用拒绝采样的方法，用来自\(q_\theta(z)\)的样本进行近似。这种方法就是拉奥-布莱克威尔化(Rao-Blackwellization)，能够有效减少方差。

5. 重参数化技巧

重参数化技巧用于降低得分函数估计器的方差，前提是\(\tilde{L}(\theta, z)\)对\(z\)可微，并且可以通过先从一个与\(\theta\)无关的噪声分布\(q_0\)中采样\(\epsilon\)，然后通过确定性和可微的函数\(z = g(\theta, \epsilon)\)转换得到\(z\)。
例如，可以从标准正态分布中采样：
\[z = g(\theta, \epsilon) = \mu + \sigma \epsilon\]

其中\(\theta = (\mu, \sigma)\)。

我们可以将目标函数重写为：
\[L(\theta) = \mathbb{E}_{q_\theta(z)}\left[\tilde{L}(\theta, z)\right] = \mathbb{E}_{q_0(\epsilon)}\left[\tilde{L}(\theta, g(\theta, \epsilon))\right]\]

由于\(q_0(\epsilon)\)与\(\theta\)无关，可以将梯度算子推入期望中，从而获得：
\[\nabla_\theta L(\theta) = \mathbb{E}_{q_0(\epsilon)}\left[\nabla_\theta \tilde{L}(\theta, g(\theta, \epsilon))\right]\]

通过蒙特卡洛方法进行近似：
\[\nabla_\theta L(\theta) \approx \frac{1}{S} \sum_{s=1}^{S} \nabla_\theta \tilde{L}(\theta, g(\theta, \epsilon_s))\]

当\(\tilde{L}\)依赖于\(\theta\)和噪声样本\(z\)时，需要使用总导数计算梯度。对于形式为\(\tilde{L}(\theta_1, \ldots, \theta_d, z_1(\theta), \ldots, z_d(\theta))\)的函数，其对\(\theta_i\)的总导数为：
\[\frac{\partial \tilde{L}}{\partial \theta_i}\bigg|_{TD} = \frac{\partial \tilde{L}}{\partial \theta_i} + \sum_j \frac{\partial \tilde{L}}{\partial z_j} \frac{\partial z_j}{\partial \theta_i}\]

进而得到：
\[\nabla_\theta \tilde{L}(\theta, z)\bigg|_{TD} = \nabla_z \tilde{L}(\theta, z) J + \nabla_\theta \tilde{L}(\theta, z)\]

其中，\(J\)为噪声变换的雅可比矩阵：\(J = \frac{\partial z}{\partial \theta}\)，这也是一种计算方法。

特别的，在变分推断中，ELBO（证据下界）目标形式为：
\[\tilde{L}(\theta, z) = \log p(z, x) - \log q(z|\theta)\]

梯度为：
\[\nabla_\theta \tilde{L}(\theta, z) = \nabla_z \left[\log p(z, x) - \log q(z|\theta)\right] J - \nabla_\theta \log q(z|\theta)\]

这里第一项是通过生成样本\(z\)对目标的间接影响，第二项是\(\theta\)对目标的直接影响。第二项在期望上为零，但在有限样本中可能非零。为了减少方差，可以使用“断开”的\(\theta'\)替代\(\theta\)来计算：
\[g = \nabla_\theta \left[\log p(z, x) - \log q(z|\theta')\right]\]

其它项如下：
\[\epsilon \sim q_0(\epsilon) \\ z = g(\epsilon, \theta) \\θ′=stop-gradient(θ)\]

这被叫做sticking the landing or STL estimator。需要指出的，这不一定比不忽略第二项的效果更好，实际中可以使用这两者的加权平均。

6. Gumbel Softmax技巧

在处理离散变量时，传统的重参数化技巧不可用。但是，我们可以将离散变量放松为连续变量，从而实现类似的效果。

考虑一个包含\(K\)位的 one-hot 向量\(d\)，其中\(d_k \in \{0, 1\}\)且\(\sum_{k=1}^{K} d_k = 1\)。这可以用于表示一个\(K\)-元的分类变量。设\(P(d) = \text{Cat}(d|\pi)\)，其中\(\pi_k = P(d_k = 1)\)，满足\(0 \leq \pi_k \leq 1\)。我们也可以将分布参数化为\((\alpha_1, \ldots, \alpha_K)\)，其中\(\pi_k = \frac{\alpha_k}{\sum_{k' = 1}^{K} \alpha_{k'}}\)​​。我们记作\(d \sim \text{Cat}(d|\alpha)\)。

我们可以通过以下公式从该分布计算 one-hot 向量\(d\)：
\[d = \text{onehot}\left(\arg\max_k\left[\epsilon_k + \log \alpha_k\right]\right)\]

其中\(\epsilon_k \sim \text{Gumbel}(0, 1)\)，从 Gumbel 分布中采样。可以通过先采样\(u_k \sim \text{Uniform}(0, 1)\)，然后计算\(\epsilon_k = -\log(-\log(u_k))\)来得到。Gumbel-Max Trick 提供了分类分布的重参数化表示。遗憾的是，\(argmax\)的导数在边界处未定义，这使得梯度计算变得复杂。

为了克服这个问题，我们可以将\(argmax\)替换为\(softmax\)，并将离散的 one-hot 向量\(d\)替换为连续放松\(x \in \Delta^{K-1}\)，其中
\[\Delta^{K-1} = \{ x \in \mathbb{R}^K : x_k \in [0, 1], \sum_{k=1}^{K} x_k = 1 \}\]

这样我们可以写出：
\[x_k = \frac{\exp\left(\frac{\log \alpha_k + \epsilon_k}{\tau}\right)}{\sum_{k' = 1}^{K} \exp\left(\frac{\log \alpha_{k'} + \epsilon_{k'}}{\tau}\right)}\]

其中\(\tau > 0\)是温度参数。随着\(\tau \to 0\)，这个分布平滑地接近离散分布。通过将\(f(d)\)替换为\(f(x)\)，我们可以对\(x\)进行重参数化梯度计算。这允许我们在进行优化时有效地处理离散变量。

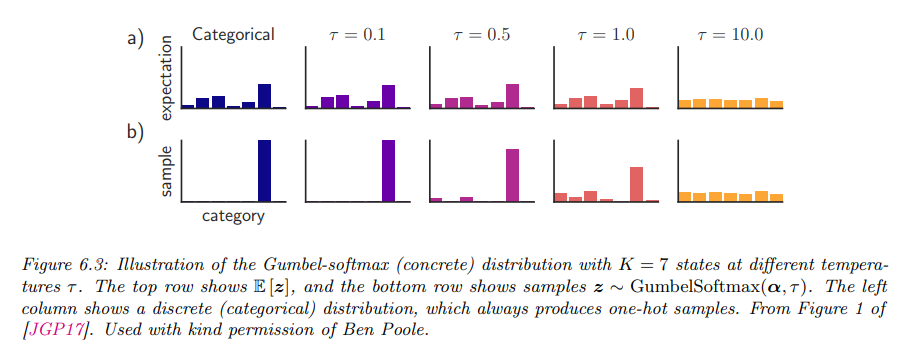
7. 直通估计器 (Straight-Through Estimator)

直通估计器主要用于近似量化信号的梯度。考虑一个阈值函数：
\[f(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}\]

这个函数没有定义良好的梯度，因为它是一个分段常数函数。

直通估计器的基本思想是，在反向传播过程中将\(g(x) = f'(x)\)的计算替换为\(g(x) = x\)。这样做的好处是可以在没有梯度的情况下为网络的训练提供一个近似值。 在实际应用中，我们有时会用硬双曲正切函数替代\(g(x) = x\)，其定义为：
\[\text{HardTanh}(x) = \begin{cases} x & \text{if } -1 \leq x \leq 1 \\ 1 & \text{if } x > 1 \\ -1 & \text{if } x < -1 \end{cases}\]

这种替代确保了反向传播的梯度不会变得过大，有助于稳定训练过程。

三、自然梯度下降

自然梯度下降（Natural Gradient Descent，NGD）是一种优化方法，主要用于优化条件概率分布\(p_\theta(y|x)\)的参数。与常规的梯度下降方法不同，NGD 通过测量引发的分布之间的距离来计算参数更新，而不是直接使用参数值的距离。这种方法特别适用于处理参数间相互作用较强的情况，比如在高维空间中的概率分布。

以两个高斯分布为例，\(p_\theta = p(y|\mu, \sigma)\)和\(p_{\theta'} = p(y|\mu', \sigma')\)。如果直接计算参数向量之间的欧几里得距离：
\[||\theta - \theta' ||^2 = (\mu - \mu')^2 + (\sigma - \sigma')^2\]

并不能反映出分布的真实变化。实际上，预测分布的形式为：
\[\exp\left(-\frac{1}{2\sigma^2}(y - \mu)^2\right)\]

这意味着，均值\(\mu\)对于不同的方差\(\sigma\)的影响大小会有区别。下图 (a-b) 说明了当方差较小和较大时，均值变化对分布的影响是不同的。明显方差小的 时候均值的影响会更大

1. 自然梯度的定义

NGD 的关键在于用 KL 散度来度量两个概率分布之间的距离。根据之前的推导，我们有：
\[D_{KL}(p_\theta(y|x) \parallel p_{\theta+\delta}(y|x)) \approx \frac{1}{2} \delta^T F_x \delta\]

其中\(F_x\)​ 是 Fisher 信息矩阵 (FIM)，定义为：
\[F_x(\theta) = -\mathbb{E}_{p_\theta(y|x)}\left[\nabla^2 \log p_\theta(y|x)\right] = \mathbb{E}_{p_\theta(y|x)}\left[(\nabla \log p_\theta(y|x))(\nabla \log p_\theta(y|x))^T\right]\]

我们可以使用平均 FIM 来计算当前和更新分布之间的平均 KL 散度：
\[F(\theta) = \mathbb{E}_{p_D(x)}\left[F_x(\theta)\right]\]

自然梯度下降通过使用 FIM 的逆作为预条件矩阵来进行参数更新：
\[\theta_{t+1} = \theta_t - \eta_t F(\theta_t)^{-1} g_t\]

其中\(g_t\)​ 是常规梯度。

因此，定义自然梯度为：
\[F^{-1} g_t = F^{-1} \nabla L(\theta_t) \equiv \tilde{\nabla} L(\theta_t)\]

2. 自然梯度下降的解释

标准的梯度下降可以被理解为在目标函数的线性近似下进行优化，同时对参数变化的\(\ell_2\)​ 范数施加惩罚。如果设定\(\theta_{t+1} = \theta_t + \delta\)，我们优化的目标为：
\[M_t(\delta) = L(\theta_t) + g_t^T \delta + \eta \frac{||\delta||^2}{2}\]

其中\(g_t\)​ 是在点\(\theta_t\)处的梯度，\(\eta\)是步长。

现在我们用基于 Fisher 信息矩阵 (FIM) 的距离替换平方距离，即：
\[||\delta||^2_F = \delta^T F \delta\]

这在whitened coordinate system中是等价的，即使用\(\phi = F^{1/2} \theta\)进行变换。我们可以得到：
\[||\phi_{t+1} - \phi_t||^2 = ||F^{1/2} (\theta_t + \delta) - F^{1/2} \theta_t||^2 = ||F^{1/2} \delta||^2 = ||\delta||^2_F\]

则新的优化目标变为：
\[M_t(\delta) = L(\theta_t) + g_t^T \delta + \eta \delta^T F \delta\]

通过求解\(\nabla_\delta M_t(\delta) = 0\)，我们可以得到更新公式：
\[\delta_t = -\eta F^{-1} g_t\]

这与自然梯度的方向一致。因此，我们可以将 NGD 视为一种trust region method，其中使用了目标函数的一阶近似，并在约束中使用 FIM 距离。

在上述推导中，我们假设 F 是常数矩阵。在大多数问题中，FIM 会在空间中的每个点上变化，这意味着我们是在一个黎曼流形的曲面上进行优化。对于某些模型，尽管我们还是使用目标函数的一阶近似，我们仍然可以高效地计算 FIM，捕捉曲率信息。

如果\(p(y|x, \theta)\)是一个指数族分布，其自然参数由\(\eta = f(x, \theta)\)计算，那么可以证明 NGD 实际上与广义高斯-牛顿（GGN）方法是相同的 。这意味着 NGD 在某些情况下可以看作是高斯-牛顿优化方法的应用。

3. 自然梯度下降 (NGD) 的优点

使用 FIM 作为预处理矩阵的一个主要优点是 FIM 总是正定的，而海森矩阵（Hessian）在鞍点处可能具有负特征值。这在高维空间中很常见，可能导致优化过程的不稳定。

同时FIM 可以通过小批量数据简单地在线近似，因为它是关于梯度向量外积的期望：
\[F_x(\theta) = \mathbb{E}_{p_\theta(y|x)} \left[ (\nabla \log p_\theta(y|x))(\nabla \log p_\theta(y|x))^T \right]\]

与之相比，研究显示，基于海森矩阵的方法对小批量数据引入的噪声非常敏感。

NGD 更新参数的方式侧重于对预测最重要的部分，这使得在不确定区域中可以采取更大的步骤，从而帮助避免陷入平坦区域或鞍点。

以一个二维高斯为例子：

在梯度下降过程中，NGD能够更快地收敛到全局最优解，相较于普通的梯度下降方法，NGD 在参数空间中的运动更加直接和高效。同时 NGD 对概率分布的参数化方式不敏感，因此即使在复杂的概率模型中（例如深度神经网络），也能保持同样的收敛效果。

一个具体的对比如下：

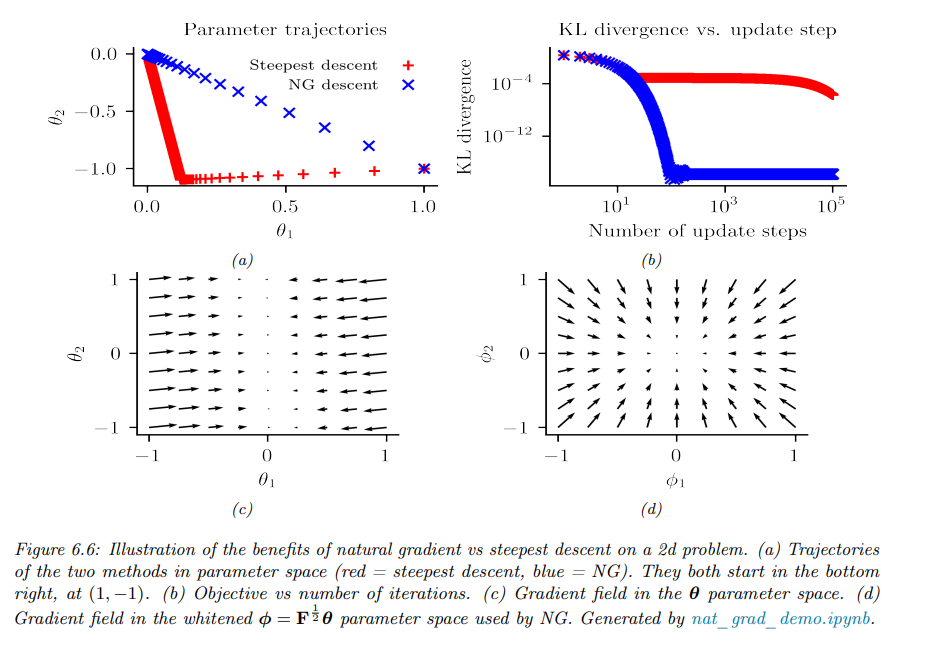
4. 近似自然梯度

NGD 的主要缺点是计算 FIM （及其逆）的计算成本较高。为了加速计算，一些方法对 FIM 的形式做出假设，以便高效地反转。例如：

有学者提出了 KFAC 方法（Kronecker Factored Approximate Curvature），该方法将深度神经网络的 FIM 近似为一个块对角矩阵，每个块是两个小矩阵的 Kronecker 积。这种方法在监督学习和强化学习中表现良好，并且已被证明在过参数化情况下能够收敛到 DNN 的全局最优解。

另一种简化方法是使用经验分布来近似 FIM。具体定义如下：
\[\begin{align*} F &= \mathbb{E}_{p_\theta(x,y)} \left[ \nabla \log p(y|x, \theta) \nabla \log p(y|x, \theta)^T \right] \\ &\approx \mathbb{E}_{p_D(x,y)} \left[ \nabla \log p(y|x, \theta) \nabla \log p(y|x, \theta)^T \right] \\ &= \frac{1}{|D|} \sum_{(x,y) \in D} \nabla \log p(y|x, \theta) \nabla \log p(y|x, \theta)^T \end{align*}\]

这种近似方法易于计算，但在平坦区域，经验 Fisher 可能变得奇异，从而导致算法陷入停滞。

另一种策略是精确计算 F，但使用截断共轭梯度（CG）方法近似计算\(F^{-1}g\)，其中每一步 CG 使用高效的海森-向量乘法方法。但这种方法可能较慢，因为进行单次参数更新需要许多 CG 迭代。

5. 自然梯度对于指数族的应用

假设损失函数\(L\)具有以下形式的期望损失：

\[L(\mu) = \mathbb{E}_{q_\mu(z)}\left[\tilde{L}(z)\right]\]

其中\(q_\mu(z)\)是具有矩参数\(\mu\)的指数族分布。

事实证明，相对于矩参数的梯度与自然参数\(\lambda\)的自然梯度是相同的。这是通过链式法则得出的：

\[\frac{d}{d\lambda} L(\lambda) = \frac{d\mu}{d\lambda} \frac{d}{d\mu} L(\mu) = F(\lambda) \nabla_\mu L(\mu)\]

其中\(L(\mu) = L(\lambda(\mu))\)，并且：

\[F(\lambda) = \nabla_\lambda \mu(\lambda) = \nabla^2_\lambda A(\lambda)\]

因此，

\[\tilde{\nabla}_{\lambda} L(\lambda) = F(\lambda)^{-1} \nabla_\lambda L(\lambda) = \nabla_\mu L(\mu)\]

接下来需要计算相对于矩参数的标注梯度。具体如何进行计算将取决于\(q\)的形式以及\(L(\lambda)\)的形式。

5.1 高斯情况下的解析计算

假设分布\(q(z) = \mathcal{N}(z|m, V)\)，我们推导如何计算与矩参数（moment parameters）相关的自然梯度。

根据Probability中对高斯分布的介绍，我们有

• 自然参数：\(\lambda^{(1)} = V^{-1}m, \quad \lambda^{(2)} = -\frac{1}{2} V^{-1}\)
• 矩参数：\(\mu^{(1)} = m, \quad \mu^{(2)} = V + mm^T\)

通过链式法则计算梯度：

对于矩参数的梯度，我们有：

\[\begin{align*} &\frac{\partial L}{\partial \mu^{(1)}} = \frac{\partial L}{\partial m} \frac{\partial m}{\partial \mu^{(1)}} + \frac{\partial L}{\partial v} \frac{\partial v}{\partial \mu^{(1)}} = \frac{\partial L}{\partial m} - 2 \frac{\partial L}{\partial v} m \\ &\frac{\partial L}{\partial \mu^{(2)}} = \frac{\partial L}{\partial m} \frac{\partial m}{\partial \mu^{(2)}} + \frac{\partial L}{\partial v} \frac{\partial v}{\partial \mu^{(2)}} = \frac{\partial L}{\partial v} \end{align*}\]

通过 Bonnet 定理和 Price 定理，我们可以得到： \[\frac{\partial}{\partial m_i} \mathbb{E}\left[ \tilde{L}(z) \right] = \mathbb{E}\left[ \frac{\partial}{\partial \theta_i} \tilde{L}(z) \right] \\\frac{\partial}{\partial V_{ij}} \mathbb{E}\left[ \tilde{L}(z) \right] = c_{ij} \mathbb{E}\left[ \frac{\partial^2}{\partial \theta_i \partial \theta_j} \tilde{L}(z) \right]\]

多变量情况下的结果：
\[\begin{align*} \nabla_{\mu^{(1)}} E_q(z) \left[ \tilde{L}(z) \right] &= \nabla_m E_q(z) \left[ \tilde{L}(z) \right] - 2 \nabla_V E_q(z) \left[ \tilde{L}(z) \right] m \\ &= E_q(z) \left[ \nabla_z \tilde{L}(z) \right] - E_q(z) \left[ \nabla^2_z \tilde{L}(z) \right] m \\ \nabla_{\mu^{(2)}} E_q(z) \left[ \tilde{L}(z) \right] &= \nabla_V E_q(z) \left[ \tilde{L}(z) \right] \\ &= \frac{1}{2} E_q(z) \left[ \nabla^2_z \tilde{L}(z) \right] \end{align*}\]

5.2 一般情况下的随机近似

在一般情况下，解析计算自然梯度可能很困难。可以使用蒙特卡洛近似。

期望损失的定义：
\[L(\mu) = \mathbb{E}_{q_\mu(z)}[\tilde{L}(z)]\]

自然梯度的表达：
\[\nabla_\mu L(\mu) = F(\lambda)^{-1} \nabla_\lambda L(\lambda)\]

期望的近似：
\[\begin{align*} F(\lambda) &= \nabla_\lambda \mu(\lambda) = \nabla_\lambda E_{q_\lambda}(z) \left[ T(z) \right] \\ \nabla_\lambda L(\lambda) &= \nabla_\lambda E_{q_\lambda}(z) \left[ \tilde{L}(z) \right] \end{align*}\]

如果\(q\)是可重参数化的，可以使用重参数化技巧将梯度推入期望算子内，从而对样本\(z\)进行采样并计算梯度。

5.3 熵的自然梯度

自然梯度\(\tilde{\nabla}_{\lambda} H(\lambda)\)表示指数族分布的熵\(H(\lambda)\)相对于自然参数\(\lambda\)的梯度，其公式为：

\[\tilde{\nabla}_{\lambda} H(\lambda) = -\nabla_\mu \mathbb{E}_{q_\mu(z)}[\log q(z)]\]

我们可以将\(q(z)\)的对数表示为：

\[\log q(z) = \log h(z) + T(z)^T \lambda - A(\lambda)\]

期望的梯度

由于\(E[T(z)] = \mu\)，我们可以对\(\log q(z)\)求\(\mu\)的梯度：

\[\nabla_\mu E_{q_\mu(z)}[\log q(z)] = \nabla_\mu E_{q(z)}[\log h(z)] + \nabla_\mu \mu^T \lambda(\mu) - \nabla_\mu A(\lambda)\]

因为\(\lambda\)是\(\mu\)的函数，我们有：

\[\nabla_\mu \mu^T \lambda = \lambda + (\nabla_\mu \lambda)^T \mu = \lambda + (F^{-1}_\lambda \nabla_\lambda \lambda)^T \mu = \lambda + F^{-1}_\lambda \mu\]

这里\(F(\lambda)\)是Fisher信息矩阵。由\(\mu = \nabla_\lambda A(\lambda)\)可得：

\[\nabla_\mu A(\lambda) = F^{-1}_\lambda \nabla_\lambda A(\lambda) = F^{-1}_\lambda \mu\]

将以上结果代入，我们得到：

\[-\nabla_\mu \mathbb{E}_{q_\mu(z)}[\log q(z)] = -\nabla_\mu \mathbb{E}_q[\log h(z)] - \lambda\]

如果我们假设\(h(z)\)是常数（这种情况在许多实际应用中成立），则得到：

\[\tilde{\nabla}_{\lambda} H(\lambda) = -\lambda\]

四、边界优化（MM）算法

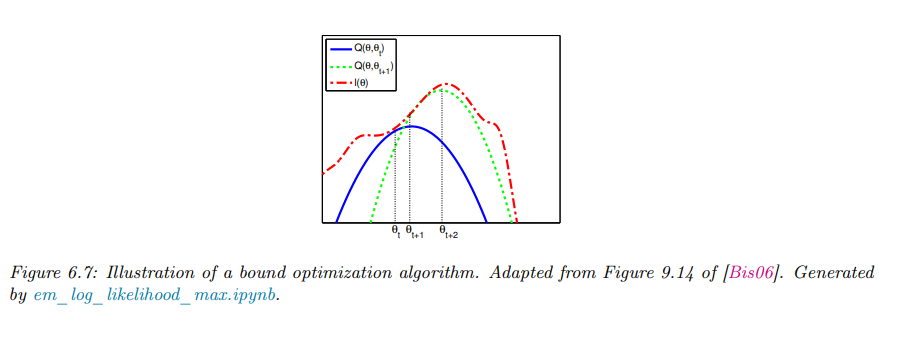
边界优化（Bound optimization）或者称为 MM（Majorize-Minimize）算法该方法主要通过构造一个次级函数\(Q(\theta, \theta^t)\)，使其成为目标函数\(\ell(\theta)\)的下界，来最大化目标函数\(\ell(\theta)\)。这种方法在许多应用中都非常有效，例如期望最大化（EM）算法和一些聚类算法。

1. 一般算法

我们的目标是最大化某个函数\(\ell(\theta)\)，MM算法的基本思路是构造一个代理函数\(Q(\theta, \theta^t)\)，使其满足以下条件

\(Q(\theta, \theta^t) \leq \ell(\theta)\) \(Q(\theta^t, \theta^t) = \ell(\theta^t)\)

如果满足这些条件，我们称\(Q\)小于等于\(\ell\)。然后在每一步进行如下更新：

\[\theta^{t+1} = \arg\max_\theta Q(\theta, \theta^t)\]

这一过程保证了原始目标函数的单调增加：

\[\ell(\theta^{t+1}) \geq Q(\theta^{t+1}, \theta^t) \geq Q(\theta^t, \theta^t) = \ell(\theta^t)\]

这保证了每一步都会提升目标函数的值。

2 示例：逻辑回归

在逻辑回归中，如果我们希望最大化的函数\(\ell(\theta)\)是一个凹函数，可以通过对其海森矩阵（Hessian）进行界定来构造有效的下界。即寻找一个负定矩阵\(B\)使得\(H(\theta) \succ B\)

通过泰勒展开，可以证明：

\[\ell(\theta) \geq \ell(\theta^t) + (\theta - \theta^t)^T g(\theta^t) + \frac{1}{2} (\theta - \theta^t)^T B (\theta - \theta^t)\]

其中\(g(\theta^t) = \nabla \ell(\theta^t)\)。

因此，可以构造以下有效的下界（这里的等于是泰勒展开前两项意义下的相等）：

\[Q(\theta, \theta^t) = \theta^T (g(\theta^t) - B\theta^t) + \frac{1}{2} \theta^T B \theta\]

对应的更新规则变为：

\[\theta^{t+1} = \theta^t - B^{-1} g(\theta^t)\]

这类似于牛顿法的更新，但使用的是固定的矩阵\(B\)，而不是每次迭代时变化的海森矩阵\(H(\theta^t)\)。

2.1 应用示例：多类逻辑回归

以多类逻辑回归为例，假设\(p(y_n = c | x_n, w)\)表示样本\(n\)属于类\(c\)的概率，公式为：

\[p(y_n = c|x_n, w) = \frac{e^{w_c^T x_n}}{\sum_{i=1}^C e^{w_i^T x_n}}\]

由于归一化条件，我们可以只学习\(C-1\)个\(w_i\)。参数\(\theta\)对应权重矩阵\(w\)。

逻辑回归的对数似然可以表示为：

\[\ell(w) = \sum_{n=1}^N \left( \sum_{c=1}^{C-1} y_{nc} w_c^T x_n - \log \sum_{c=1}^C e^{w_c^T x_n} \right)\]

其梯度和海森矩阵分别为：

\[g(w) = \sum_{n=1}^N (y_n - p_n(w)) \otimes x_n \\ H(w) = -\sum_{n=1}^N \left( \text{diag}(p_n(w)) - p_n(w) p_n(w)^T \right) \otimes (x_n x_n^T)\]

通过构造海森矩阵的下界，可以得到：

\[H(w) \succ -\frac{1}{2} \left( I - \frac{1}{C} \mathbf{1} \mathbf{1}^T \right) \otimes \left( \sum_{n=1}^N x_n x_n^T \right) \equiv B\]

这里的\(I\)是一个\((C−1)\)维的单位矩阵，而\(1\)是一个全为 1 的\((C - 1)\)维向量。在二分类的情况下，这可以变为：

\[H(w) \succ -\frac{1}{2} \left(1 - \frac{1}{2}\right) \left(\sum_{n=1}^N x_n^T x_n\right) = -\frac{1}{4} X^T X\]

这是因为\(p_n \leq 0.5\)，所以有\(- (p_n - p_n^2) \geq -0.25\)。

因此更新规则为：

\[w^{t+1} = w^t - B^{-1} g(w^t)\]

在二分类的情况下，\(g_t = \nabla \ell(w_t) = X^T (y - \mu_t)\)，则更新规则为：

\[w^{t+1} = w^t - 4(X^TX)^{-1} g^t\]

与牛顿法（IRLS）的标准更新比较：

\[w^{t+1} = w^t - H^{-1} g(w^t) = = w^t − (X^TS^tX)^{−1}g^t\]

可以看出，使用下界的MM算法在每一步的计算上会更快，因为\((X^T X)^{-1}\)可以预先计算。

3. EM算法

EM算法通过在两个步骤之间交替进行来估计模型参数：

1. E步骤（期望步骤）：估计隐藏变量或缺失值。
2. M步骤（最大化步骤）：使用完全观察到的数据计算MLE。

这个过程需要迭代，因为期望值依赖于参数，而参数又依赖于期望值。

3.1 下界

EM算法的目标是最大化观察数据的对数似然函数：

\[\ell(\theta) = \sum_{n=1}^{N} \log p(y_n | \theta) = \sum_{n=1}^{N} \log \left( \sum_{z_n} p(y_n, z_n | \theta) \right)\]

其中\(y_n\)​ 是可观察变量，\(z_n\)​ 是隐藏变量。直接优化这个对数似然函数是困难的，因为对数函数不能被推入求和符号内部。

EM算法通过引入任意分布\(q_n(z_n)\)来解决这个问题。观察数据的对数似然函数可以写为：

\[\ell(\theta) = \sum_{n=1}^{N} \log \left( \sum_{z_n} q_n(z_n) \frac{p(y_n, z_n | \theta)}{q_n(z_n)} \right)\]

利用詹森不等式（Jensen’s inequality），可以将对数函数推入期望之内，得到对数似然函数的下界：

\[\ell(\theta) \geq \sum_n \sum_{z_n} q_n(z_n) \log \frac{p(y_n, z_n | \theta)}{q_n(z_n)}\]

这可以进一步写为：

\[\ell(\theta) \geq \sum_n \mathbb{E}_{q_n}[\log p(y_n, z_n | \theta)] + H(q_n)\]

其中\(H(q)\)是概率分布\(q\)的熵。定义下界为ELBO：

\[\mathcal{L}(\theta, \{q_n\} | D) = \sum_n \mathcal{L}(\theta, q_n | y_n)\]

优化这个下界是变分推断的基础。

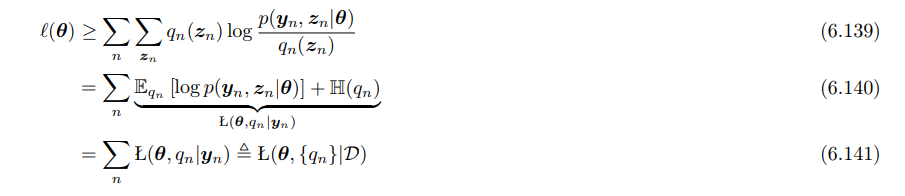
3.2 E步骤

下界的每一项可以写为：

\[\mathcal{L}(\theta, q_n | y_n) = \sum_{z_n} q_n(z_n) \log \frac{p(y_n, z_n | \theta)}{q_n(z_n)}\]

这可以分解为：

\[\begin{align*} \mathcal{L}(\theta, q_n | y_n) &= \sum_{z_n} q_n(z_n) \log \frac{p(y_n, z_n | \theta)}{q_n(z_n)} \\ &= \sum_{z_n} q_n(z_n) \log \frac{p(z_n | y_n, \theta) p(y_n | \theta)}{q_n(z_n)} \\ &= \sum_{z_n} q_n(z_n) \log \frac{p(z_n | y_n, \theta)}{q_n(z_n)} + \sum_{z_n} q_n(z_n) \log p(y_n | \theta) \\ &= -D_{KL}(q_n(z_n) \parallel p(z_n | y_n, \theta)) + \log p(y_n | \theta) \end{align*}\]

因此，我们可以通过将每个\(q_n\)设置为：

\[q_n^* = p(z_n | y_n, \theta)\]

来最大化下界\(\mathcal{L}(\theta, \{q_n\} | D)\)。这就是E步骤。此时，ELBO就等于最大似然：

\[\mathcal{L}(\theta, \{q_n^*\} | D) = \sum_n \log p(y_n | \theta) = \ell(\theta | D)\]

3.3 M步骤

在M步骤中，我们需要最大化：

\[\mathcal{L}(\theta, \{q_n^t\})\]

由于熵项\(H(q_n)\)在\(\theta\)方面是常数，因此在M步骤中可以忽略这些项。我们剩下的部分是：

\[\ell_t(\theta) = \sum_n \mathbb{E}_{q_n^t(z_n)} [\log p(y_n, z_n | \theta)]\]

如果联合概率属于指数族，我们可以将其重写为：

\[\ell_t(\theta) = \sum_n \mathbb{E}[T(y_n, z_n)]^T \theta - A(\theta)\]

在M步骤中，我们最大化期望的完整数据对数似然函数，得到：

\[\theta^{t+1} = \arg \max_{\theta} \sum_n \mathbb{E}_{q_n^t} [\log p(y_n, z_n | \theta)]\]

对于指数族的情况，最大化可以通过匹配期望充分统计量的矩来闭合地求解。

3.4 例子

书中以缺失数据的MLE为例子：

3.5 扩展EM算法

• Variational EM （变分 EM）

变分 EM 是 EM 算法的一种变体。在 E 步中，我们使用一种称为变分推断的方法来近似后验分布。具体来说，在 E 步中，我们选择一个分布\(q^*_n\)​ 来最小化\(q_n\)​ 与真实后验分布\(p(z_n | x_n, \theta)\)之间的 KL 散度：

\[q^*_n = \arg \min_{q_n \in Q} D_{KL}(q_n \| p(z_n | x_n, \theta))\]

这实际上是一个变分推断过程。在这种情况下，\(Q\)是我们定义的一个分布族。如果分布族\(Q\)足够灵活，能够包含真实的后验分布，那么\(q_n\)可以接近\(p(z_n | x_n, \theta)\)，使得 KL 散度趋于 0。

为了计算简便，通常选择较为简单的分布族。例如，即使真实后验分布是相关的，我们可能也会假设\(q_n(z_n) = N(z_n | \mu_n, \text{diag}(\sigma_n))\)（即独立的多元正态分布）。

在这种情况下，使用有限的分布族\(Q\)代替真实的后验分布，称为 变分 EM。变分 EM 不一定能保证增加实际的对数似然值，但可以单调增加变分下界。

• Hard EM

在变分 EM 的框架下，假设我们使用的是一个退化的后验近似，即仅考虑后验分布的一个点估计：

\[q(z | x_n) = \delta_{z_{\hat{n}}}(z)\]

这样\(z_{\hat{n}} = \arg \max_z p(z | x_n)\)，即后验分布的最大值点。这样的方式称为 Hard EM，即在 E 步中忽略了\(z_n\)​ 的不确定性。

这种方法的缺点是，它很容易导致过拟合，特别是在隐变量的数量与数据量成正比的情况下。

• Monte Carlo EM

当 E 步难以求解时，可以使用 Monte Carlo 方法来近似期望的充分统计量。具体地，我们从后验分布中采样：

\[z^s_n \sim p(z_n | x_n, \theta^{(t)})\]

然后计算每个样本的充分统计量，最后将结果取平均。这种方法称为 Monte Carlo EM（MCEM）。

每个 E 步中都要等待 MCMC 收敛会非常耗时。另一种选择是使用随机近似法（stochastic approximation），即在 E 步中只进行简短的采样，之后进行部分参数更新。这种方法称为 随机近似 EM（Stochastic Approximation EM），通常比 MCEM 更快。

• Generalized EM （广义 EM）

在某些情况下，我们可以精确地执行 E 步，但无法精确地执行 M 步。然而，即使不精确执行 M 步，也可以通过增加期望的完整数据对数似然来单调增加对数似然。这种情况下，我们可以只进行“部分” M 步，例如执行几个梯度下降步。这种方法称为 广义 EM（GEM）。

具体地，我们可以使用一个牛顿-拉弗森（Newton-Raphson）步骤来更新参数：

\[\theta^{(t+1)} = \theta^{(t)} - \eta_t H_t^{-1} g_t\]

其中，\(0 < \eta_t \leq 1\)是步长，\(g_t\)和\(H_t\)​ 分别表示梯度和 Hessian 矩阵：

\[g_t = \frac{\partial}{\partial \theta} Q(\theta, \theta^{(t)}) \big|_{\theta = \theta^{(t)}}​ \\H_t = \frac{\partial^2}{\partial \theta \partial \theta^T} Q(\theta, \theta^{(t)}) \big|_{\theta = \theta^{(t)}}\]

当\(\eta_t = 1\)时，这被称为梯度 EM 算法。为了加速算法，也可以采用较大的步长，如在准牛顿 EM 中使用 BFGS 近似替代 Hessian。

五、贝叶斯优化

贝叶斯优化（Bayesian Optimization）简称 BayesOpt，它是一种基于模型的黑盒优化方法，旨在优化难以评估的目标函数\(f : X \to R\)的情形。（例如模拟成本比较高、训练复杂模型等）。由于计算代价高，我们希望尽可能少地调用目标函数，即减少查询\(x\)的次数。因此，贝叶斯优化通过构建一个代理函数来近似目标函数\(f\)并在每次查询进行选择，避免重复昂贵的函数评估。

贝叶斯优化的核心思想是：在构建代理函数的基础上权衡探索（exploration）和利用（exploitation）。

• 探索指的是在不确定的区域进行查询，以改善对代理模型的整体了解；
• 利用指的是在目标函数\(f(x)\)预期较高的区域查询，以更快地找到最优点。这种权衡称为探索-利用困境。

假设目标函数的查询数据集为\(D_n = \{(x_i, y_i) : i = 1, ..., n\}\)，其中\(y_i = f(x_i) + \epsilon_i\)，其中\(\epsilon_i\)​ 是一个可能的噪声项。基于此数据集构建的代理模型可以估计\(f\)的概率分布\(p(f | D_n)\)。每一步优化中，我们通过采集函数（acquisition function）来选择下一个查询点\(x_{n+1}\)​，采集函数根据模型不确定性和目标值的期望收益计算出最优的查询点。

1. 顺序模型优化（Sequential Model-Based Optimization, SMBO）

贝叶斯优化是一种顺序模型优化（SMBO）的方法。在每一次迭代中，贝叶斯优化通过一个已标记的数据集\(D_n = \{(x_i, y_i) : i = 1, ..., n\}\)来更新对代理模型的估计。该数据集记录了每个查询点\(x_i\)​ 及其对应的函数值\(y_i = f(x_i) + \epsilon_i\)。基于此数据集，我们可以估计目标函数的概率分布\(p(f | D_n)\)，然后使用采集函数\(\alpha(x; D_n)\)来决定下一个查询点\(x_{n+1}\)​。查询\(x_{n+1}\)​ 获得\(y_{n+1} = f(x_{n+1}) + \epsilon_{n+1}\)后，我们更新对目标函数的估计，然后重复上述步骤。

贝叶斯优化的主要步骤包括：

• 代理模型的构建和更新：代理模型用于近似目标函数\(f\)的后验分布\(p(f | D_n)\)。
• 采集函数的定义和优化：采集函数\(\alpha(x; D_n)\)用于评估查询点的潜在收益，从而决定下一个查询点的位置。

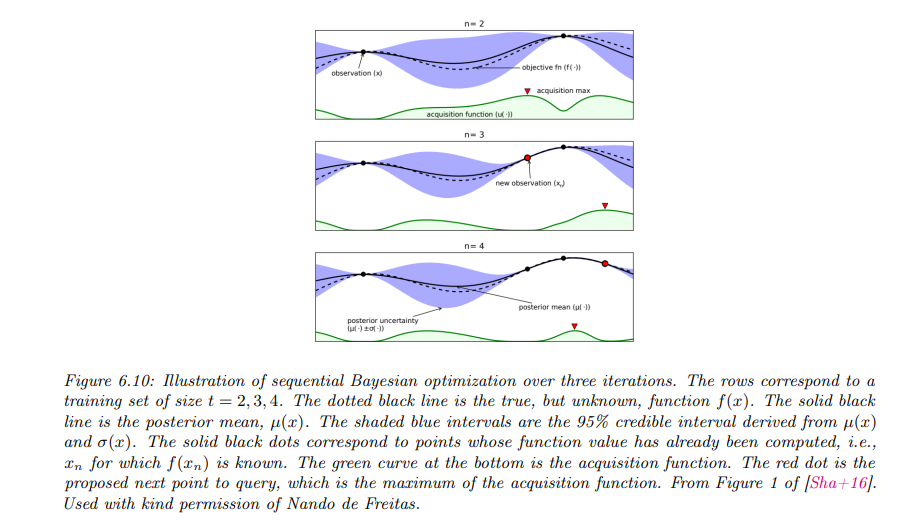
下图展示了贝叶斯优化的运行过程：

• 在初始时，通过两个已查询点\(x_1\)和\(x_2\)​ 确定了代理模型在这些位置上的函数值，模型在这两点附近的不确定性趋近于0。
• 采集函数（绿色曲线）在已查询点的位置值为 0，并在代理模型不确定性较高的区域达到最大值。
• 之后的迭代中，随着新的点被查询和观测，模型逐渐减少了对真实函数的估计不确定性，逐步逼近目标函数的全局最优解。

2. 代理函数

对于代理函数，主要有高斯过程（Gaussian Processes, GPs）、贝叶斯神经网络（Bayesian Neural Networks, BNNs）等。

• 高斯过程（GPs）

高斯过程是一种常用的代理函数。在 GP 中，\(p(f(x)|D_n)\)被建模为正态分布\(N(f|\mu_n(x), \sigma_n^2(x))\)，其中均值\(\mu_n(x)\)和方差\(\sigma_n(x)\)可以通过训练数据集\(D_n\)​ 推导得出。

核函数\(K_\theta(x, x')\)用于度量输入点\(x\)和\(x′\)之间的相似度。相似度高的点对应该有相似的函数值，因此可以正相关。高斯过程据此在训练点之间内插值（有时甚至可以外推）。核函数的选择至关重要。通常可以通过最大化边际似然来估计核参数\(\theta\)，或者使用贝叶斯推断来近似边际化\(\theta\)。

高斯过程在数据较少时效果很好，支持闭式的贝叶斯更新，但计算代价为\(O(N^3)\)（其中\(N\)为样本数），对于大量函数评估来说会很慢。有一些方法可以将计算复杂度降低至\(O(NM^2)\)，其中\(M\)是可选参数，但会牺牲精度。

• 贝叶斯神经网络（BNNs）

贝叶斯神经网络是高斯过程的一种自然替代。使用线性回归时，可以高效地进行精确的贝叶斯推断。但若使用非线性模型（如深度神经网络，DNN），则需使用近似推断。

BNNs 提供了一个在贝叶斯优化中替代 GPs 的方式，因为它们能够建模非线性关系，且在大数据量下通常更高效。关于贝叶斯网络的具体内容会后面进行学习。

还可以使用其他形式的回归模型。例如，随机森林集成模型在贝叶斯优化中表现良好，因为它们可以处理条件参数空间，但需要bootstrapping来获得不确定性估计，计算较慢。

3. 采集函数

采集函数用来评估每个可能的查询点的预期效用。一般表示为：

\[\alpha(x|D_n) = \mathbb{E}_{p(y|x,D_n)}[U(x, y; D_n)]\]

其中：

\(y = f(x)\)是在点\(x\)处未知函数的值， \(U\)是效用函数，它决定不同采集函数的形式。

下面介绍一些常见的采集函数。

3.1 改进概率（Probability of Improvement, PI）

改进概率用于评估某一点是否可能带来比当前最优观测值更好的结果。定义如下：

首先，设定目前的最优值（incumbent）为：
\[M_n = \max_{i=1}^n y_i\]

如果观测是有噪声的，可以选择最高均值代替最大观测值。定义效用函数：

\[U(x, y; D_n) = I(y > M_n)\]

其中\(I(\cdot)\)是指示函数，即当\(y\)超过当前最优值\(M_n\)​ 时，产生效用 1，否则为 0。

因此，PI 采集函数可以表示为：
\[\alpha_{\text{PI}}(x; D_n) = p(f(x) > M_n | D_n)\]

若代理模型是高斯过程，可以得到 PI 的闭式解（就是简单的高斯分布求概率）：

\[\alpha_{\text{PI}}(x; D_n) = \Phi\left(\gamma_n(x, M_n)\right)\]

\[\gamma_n(x, \tau) = \frac{\mu_n(x) - \tau}{\sigma_n(x)}\]

其中：

\(\Phi\)是标准正态分布的累积分布函数（CDF）， \(\mu_n(x)\)和\(\sigma_n(x)\)分别是高斯过程在\(x\)处的均值和标准差。

3.2 期望改进（Expected Improvement, EI）

期望改进考虑的是改进的量，而不仅仅是是否产生改进。定义效用函数为 ：

\[U(x, y; D_n) = (y - M_n)I(y > M_n)\]

这样只有\(y > M_n\)​ 时才会有正值的效用。

因此，EI 采集函数表示为：
\[\alpha_{\text{EI}}(x; D_n) = \mathbb{E}_{D_n}[(f(x) - M_n)I(f(x) > M_n)]\]

在高斯过程模型下，EI 有以下闭式解：

\[\alpha_{\text{EI}}(x; D_n) = (\mu_n(x) - M_n)\Phi(\gamma) + \sigma_n(x)\phi(\gamma)\]

其中：

\(\phi\)是标准正态分布的概率密度函数 \(\gamma = \gamma_n(x, M_n) = \frac{\mu_n(x) - M_n}{\sigma_n(x)}\)

我们可以注意到EI 的两个部分：

• 第一项\((\mu_n(x) - M_n)\Phi(\gamma)\)促进利用（选择均值高的点）
• 第二项\(\sigma_n(x)\phi(\gamma)\)则促进探索（选择方差大的点）。

如果无法计算预测方差，可以使用蒙特卡洛方法近似：

\[\alpha_{\text{EI}}(x; D_n) \approx \frac{1}{S} \sum_{s=1}^S \max(\mu_n^s(x) - M_n, 0)\]

3.3 上置信界（Upper Confidence Bound, UCB）

上置信界通过计算函数的上置信区间来决定评估点。其采集函数定义为：

\[\alpha_{\text{UCB}}(x; D_n) = \mu_n(x) + \beta_n \sigma_n(x)\]

其中\(\beta_n\)​ 控制置信区间的宽度。在高斯过程代理模型下，这种方法称为 GP-UCB。

3.4 汤普森采样（Thompson Sampling）

汤普森采样尝试直接从后验分布中采样，以找到潜在的最优点。采集函数定义为：

\[\alpha(x; D_n) = \mathbb{E}_{p(\theta|D_n)} \left[ I\left( x = \arg\max_{x'} f_\theta(x') \right) \right]\]

通过从\(p(\theta|D_n)\)中采样一个\(\tilde{\theta}\)，我们选择最大化\(f_{\tilde{\theta}}(x)\)的点。对于高斯过程，采样会比较复杂，因此应用起来需要特殊的技术。

3.5 熵搜索（Entropy Search）

熵搜索直接最小化对最优点位置的不确定性。熵搜索的效用函数定义为：

\[U(x, y; D_n) = H(x^*|D_n) - H(x^*|D_n \cup \{(x, y)\})\]

其中\(H(x^*|D_n)\)是后验分布\(p^*(x|D_n)\)的熵。熵搜索的采集函数为：

\[\alpha_{\text{ES}}(x; D_n) = \mathbb{E}_{p(y|x, D_n)}[U(x, y; D_n)] = H(x^*|D_n) - \mathbb{E}_{p(y|x, D_n)}[H(x^*|D_n \cup \{(x, y)\})]\]

通过预测熵搜索（Predictive Entropy Search, PES），可以使用互信息的对称性来简化该采集函数：

\[\alpha_{\text{PES}}(x; D_n) = H(y|D_n, x) - \mathbb{E}_{x^*|D_n}[H(y|D_n, x, x^*)]\]

在这里，可以通过汤普森采样来近似积分。

3.6 知识梯度 (Knowledge Gradient)

知识梯度获取函数的核心思想是：通过考虑在查询一个新点后，更新我们的后验分布，然后基于新的分布进一步寻找最大值。这种方法不只是关注当前步骤的最大化，而是展望两步，从而达到长远的优化效果。

假设我们在点\(x\)查询后，得到了新的观测值\(y\)，可以根据新的信念找到下一个可能的最佳值：
\[V_{n+1}(x, y) = \max_{x'} \mathbb{E}_{p(f|x, y, D_n)} [f(x')]\]

其中\(V_{n+1}(x, y)\)表示在位置\(x\)查询并得到结果\(y\)后，下一步所能达到的最大值。

由于我们在进行查询时并不知道真实的\(y\)值，因此需要对所有可能的\(y\)取期望，以得出在查询\(x\)位置后的期望的增益：
\[V_{n+1}(x) = \mathbb{E}_{p(y|x, D_n)} [V_{n+1}(x, y)]\]

知识梯度获取函数的定义如下：
\[\alpha_{KG}(x; D_n) = \mathbb{E}_{D_n} \left[(V_{n+1}(x) - M_n) \cdot I(V_{n+1}(x) > M_n)\right]\]

这里\(M_n = \max_{i=1}^n y_i\)，​ 是当前已观察到的最佳值（即，迄今为止观察到的最大值）。该函数的定义类似于期望提升（Expected Improvement, EI），区别在于知识梯度考虑的是观察新点后可以利用的新知识，而不仅仅是找到一个新的最大值。

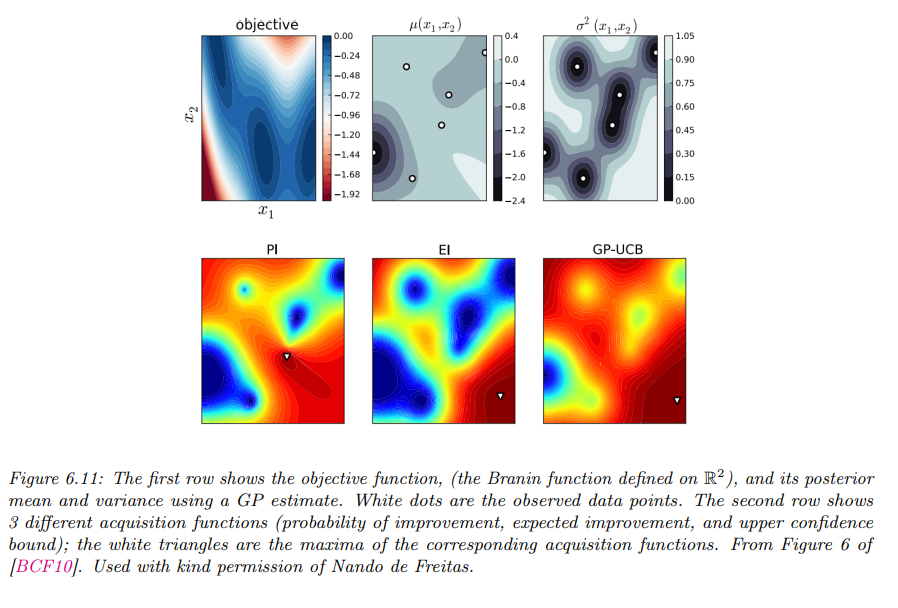
下面是上面方法之间在一个实践中的对比：

六、无梯度优化

无梯度优化（DFO，Derivative-free Optimization）指的是在不知道函数的导数信息时如何进行优化。根据目标函数的评估成本，无梯度优化可以分为贝叶斯优化（适用于高评估成本的情况）和随机局部搜索或进化搜索（适用于低评估成本的情况）。贝叶斯优化已经讲过了，所以下面的内容主要集中在随机局部搜索或进化搜索。

1. 局部搜索（Local Search）

局部搜索是一类启发式优化算法，旨在寻找离散、非结构化搜索空间中的全局最大值。传统的梯度更新形式为：

\[\theta_{t+1} = \theta_t + \eta_t d_t\]

但在无梯度优化中无法使用此更新形式，因此使用一个离散版本的更新方式。具体来说，更新的公式为：

\[L(x)x_{t+1} = \arg \max_{x \in \text{nbr}(x_t)} L(x)\]

其中\(\text{nbr}(x_t) \subset X\)表示\(x_t\)的邻域，这一方法被称为爬山算法（hill climbing）、最陡上升（steepest ascent）或贪心搜索。

若一个点的邻域包含整个搜索空间，则上面公式可在一步内返回全局最优解，但通常这种邻域过大，难以完全搜索。因此，通常会定义局部邻域。例如，在8皇后问题中，目标是将8个皇后放置在 8×8 棋盘上，使它们互不攻击。8皇后的状态空间\(X = 64^8\)，但由于约束，只有大约 17M 个可行状态。定义每个状态的邻域为所有通过将一个皇后移动到同列其他位置而生成的状态，因此每个状态有 56 个邻居。然而，随机生成的初始状态通过最陡上升法只能成功解决14%的问题，并且在失败时会停留在局部最优解处。

1.1 随机局部搜索（Stochastic Local Search）

爬山算法是一种贪心算法，因为它在邻域内选择最优点。这种方法容易卡在局部最优解。为了减少这种情况，一个解决方法是将目标在每一步的最大化从确定性转变为随机化。具体而言，可以定义邻居的概率分布，概率与邻居改进的程度成正比，从而随机采样一个邻居点。这被称为随机爬山法（stochastic hill climbing）。

如果逐渐减小该概率分布的熵，使算法逐渐趋于贪心，则得到模拟退火算法（simulated annealing）。另一种方法是使用贪心爬山算法，但在遇到局部最优解时，从一个新的随机起点重新开始。这种方法称为随机重启爬山法（random restart hill climbing）。例如在8皇后问题中，如果每次爬山搜索的成功概率为\(p \approx 0.14\)，期望需要\(R = 1/p \approx 7\)次重启才能找到有效解。

1.2 禁忌搜索（Tabu Search）

爬山法在达到局部最优或平台时会停止。虽然可以通过随机重启来避免这种情况，但会丢弃已有的信息。禁忌搜索（Tabu Search）是一种更智能的替代方法。禁忌搜索允许移动到得分下降的状态，只要该状态之前没有访问过。为此，我们维护一个禁忌表（tabu list），记录最近访问的\(\tau\)个状态，从而强制算法探索新的状态，增加逃离局部最优解的机会。

禁忌搜索达到局部最高点\(x_t\)​ 时，会移动到邻居\(x_{t+1} \in \text{nbr}(x_t)\)，该点得分较低。接着它会移动到之前状态的邻居\(x_{t+2} \in \text{nbr}(x_{t+1})\)，禁忌表阻止它返回到峰顶，从而使它继续探索，直到找到新的峰顶，或达到最多非改进步数\(c_{\text{max}}\)​。

在8皇后问题中，禁忌搜索能将解决成功率从14%提高到94%，平均每个成功实例需要21步，失败实例需要64步。

2. 模拟退火 (Simulated Annealing)

模拟退火是一种随机局部搜索算法，通常用于寻找黑箱函数\(E(x)\)的全局最小值，这里的\(E\)被称为能量函数。模拟退火的灵感来源于物理学中的退火过程，通过逐步降低“温度”来达到目标。

将能量函数\(E(x)\)转换为状态概率分布：
\[p(x) = \exp(-E(x))\]

这里的\(p(x)\)是未归一化的概率分布，目的是构建一个与能量成反比的概率分布。

模拟退火每次会使用一种变体的 Metropolis-Hastings 算法（采样算法）来从概率分布中采样。每次迭代中，算法会选择一个新的候选状态\(x′\)，然后按照概率接受或拒绝该状态。接受概率由能量差值和当前“温度”决定：
\[\text{接受概率} = \min \left( 1, \exp \left( \frac{E(x) - E(x')}{T} \right) \right)\]

其中\(T\)是“温度”参数，随着迭代次数增加逐渐减小。在高温阶段，算法倾向于接受更差的解，以避免陷入局部极小值；在低温阶段，逐渐收敛于全局最优解。

3. 进化算法 (Evolutionary Algorithms)

进化算法是一类仿生算法，模拟自然选择和遗传进化的过程，以优化复杂目标函数。这类算法通常使用一个种群\(S_t\)来表示候选解的集合。

进化算法的主要组成部分

• 适应度 (Fitness)： 每个候选解的“适应度”是其目标函数的值，即评估该解的好坏。
• 选择函数 (Selection Function)： 从当前种群中选择适应度较高的成员作为“父代”生成“子代”。常见的选择策略包括：
  • 截断选择 (Truncation Selection)： 从适应度最高的前\(K\)个成员中随机选择父代。
  • 锦标赛选择 (Tournament Selection)： 每次从种群中随机选择\(K\)个成员，选择适应度最高的个体作为父代。
  • 适应度比例选择 (Fitness Proportionate Selection)： 按照个体适应度的相对比例选择父代（也叫轮盘选择）。
• 重组 (Recombination) 和变异 (Mutation)： 生成新候选解的关键操作：
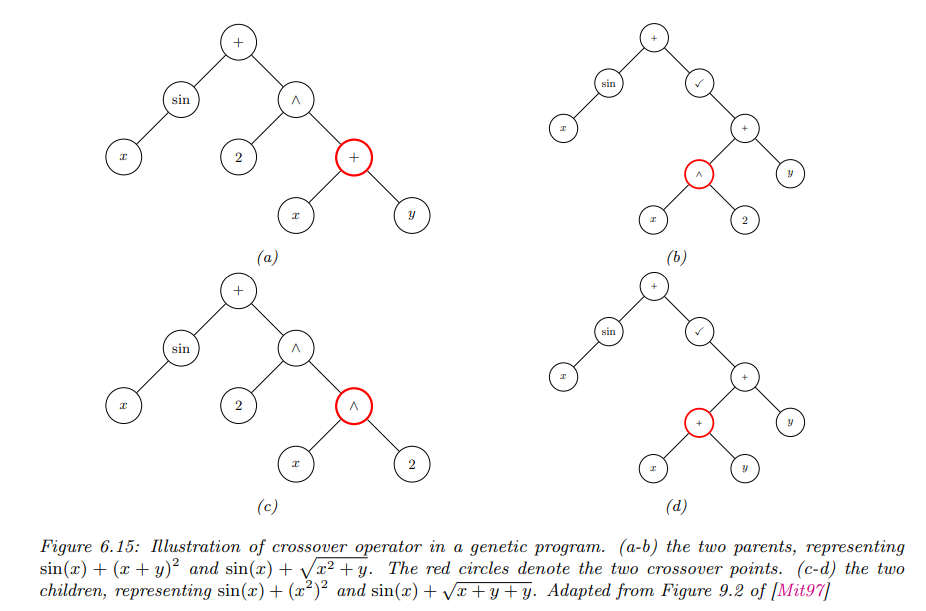
  • 交叉 (Crossover)： 对两个父代进行基因交换，产生子代。例如在遗传算法中，每个个体可以表示为二进制或整数向量，随机选择切割点并交换父代的子串。
  • 变异 (Mutation)： 对单个个体进行小范围随机改变，用于增加种群多样性。

常见的进化算法如下：

• 遗传算法 (Genetic Algorithm, GA)： 使用二进制或整数表示个体，通过交叉和变异产生新的个体，如上图。
• 遗传编程 (Genetic Programming, GP)： 使用树状结构表示个体，适合生成结构化对象或程序，如下图。
• 代理辅助进化算法 (Surrogate-assisted EA)： 使用近似模型替代真实的目标函数，以减少评估开销。
• 记忆算法 (Memetic Algorithm)： 结合进化算法和局部搜索，提升求解效率。

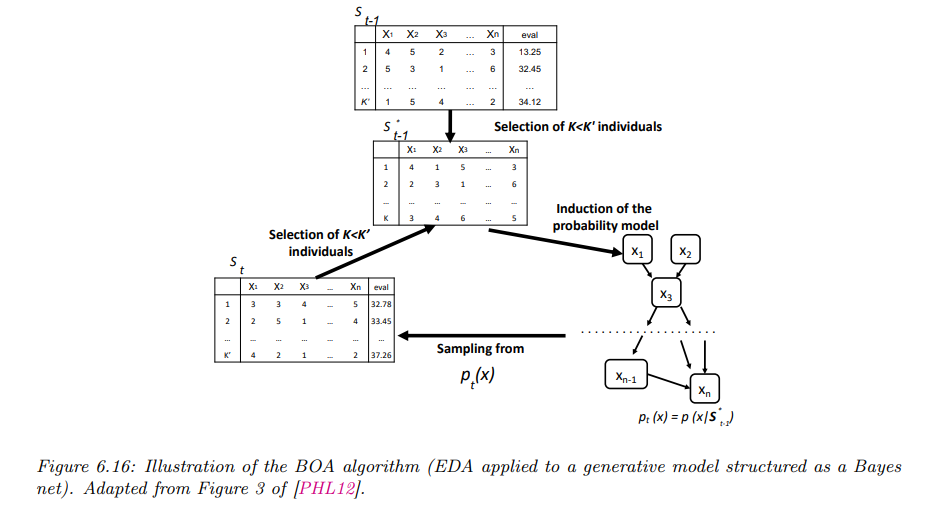
4. 分布估计算法

分布估计算法（Estimation of Distribution Algorithms, EDA）是一种进化算法（EA）的变体。EDA 的主要思想是用概率模型来表示高适应度解的分布，而不是通过基因操作（如交叉、变异）来生成新解。

传统的进化算法依赖遗传操作来保持和生成候选解的种群，而 EDA 则采用显式的概率模型来估计解的分布。在每次迭代中，EDA 从当前的概率模型中采样生成候选解，选出最优的部分解，然后基于这些解更新概率模型，从而使其逐步向最优解靠近。

具体的 EDA 操作步骤：

• 候选解采样：从当前模型\(p(x|\theta_t)\)中采样\(K' > K\)个候选解，构成种群\(S_t = \{x_k \sim p(x|\theta_t)\}\)。
• 选择操作：用适应度函数对这些候选解排序，选择出最优的\(K\)个解，记为\(S^*_t\)（截断选择）。
• 更新概率模型：利用最大似然估计（MLE）将新模型\(p(x|\theta_{t+1})\)拟合到\(S^*_t\)​ 上，得到下一代的解分布。

EDA 本质上是通过最小化\(S^*_t\)​ 的经验分布与新模型分布\(p(x|\theta_{t+1})\)的交叉熵来进行更新，因此与交叉熵法（CEM）有一定联系。对比来看，交叉熵法通常假设模型为多元高斯分布\(N(x|\mu, \Sigma)\)，而 EDA 更加通用。

在实际应用中，为了表示解空间中的变量依赖性，可以选择更加复杂的概率模型。

• 对于连续变量，可以使用多元高斯模型\(p(x) = N(x|\mu, \Sigma)\)，此方法被称为多元正态估计算法（EMNA）。
• 对于离散变量：可以用概率图模型（如树结构、贝叶斯网络）来捕捉变量之间的依赖关系。Chow-Liu 算法可以用于树结构的学习，而更复杂的图模型结构也可以通过 BOA 等算法学习。

随着深度学习的应用，可以使用深度生成模型来表示解分布。例如，可以使用去噪自编码器、NADE、DNN 回归模型、RBM（受限玻尔兹曼机）和 VAE（变分自编码器）等。

4.1 示例：UMDA

考虑一个简单的例子，目标空间是长度为\(D\)的二进制字符串，适应度函数为

\[f(x) = \sum_{d=1}^D x_d\]

其中\(x_d \in \{0, 1\}\)（称为 one-max 函数）。一个简单的概率模型是完全分解的模型：

\[p(x|\theta) = \prod_{d=1}^D \text{Ber}(x_d|\theta_d)\]

这称为单变量边际分布算法（UMDA）。对于这种伯努利分布，可以通过统计\(S^*_t\)​ 中各位置的 1 的比例来估计参数：

\[\hat{\theta}_{d, t+1} = \frac{1}{N_t} \sum_{k=1}^K I(x_{k, d} = 1)\]

其中\(K = |S^*_t|\)，表示选择的候选解数量。为了平滑参数更新，可以使用如下增量更新公式：

\[\hat{\theta}_{d, t+1} = (1 - \eta_t) \hat{\theta}_{d, t} + \eta_t \theta_{d, t}\]

其中，\(\eta_t\)是学习率，\(\theta_{d, t}\)是第\(t\)代选择子集中第\(d\)位为 1 的比例。这个更新方法称为基于种群的增量学习（PBIL）。

4.2 交叉熵法（CEM）

交叉熵法是一种特殊的分布估计算法（EDA），其中种群由多元高斯分布表示。算法的主要步骤如下：

• 设置均值和协方差：\(\mu_{t+1}\)和\(\Sigma_{t+1}\)被设置为\(S^*_{t+1}\)的经验均值和协方差，\(S^*_{t+1}\)是前 K 个样本。
• 优化问题： 在 CEM 中，我们希望最大化以下目标：
  \[\theta_{t+1} = \arg\max_{\theta} \sum_{i \in S_t} p_t(i) \log p(x_{t,i} | \theta)\]

其中\(p_t(i)\)是与选择的样本\(S^*_t\)相关的概率分布。

5. 进化策略（Evolutionary Strategies, ES）

进化策略是一种基于分布的优化方法，其中种群的分布用高斯分布表示。与 CEM 不同，ES 通过对期望目标的梯度上升来更新参数，而不是使用 MLE。主要步骤如下：

• 平滑目标函数：
  \[L(\theta) = \mathbb{E}_{p(x|\theta)}[f(x)]\]
• 计算梯度： 使用 REINFORCE 估计器计算梯度：
  \[\nabla_\theta L(\theta) = \mathbb{E}_{p(x|\theta)}[f(x) \nabla_\theta \log p(x|\theta)]\]

这个期望可以通过蒙特卡罗采样进行近似。

当概率模型属于指数族时，可以计算自然梯度，通常收敛速度更快。自然进化策略（Natural Evolution Strategies, NES）使用自然梯度替代“普通”梯度，以加速优化。

CMA-ES 是一种 NES，主要特征在于它以加权的方式更新均值和协方差。具体步骤如下：

1. 计算加权均值： 新均值设为当前样本的加权 MLE。
2. 更新协方差： 使用“进化路径”来累积搜索方向，更新协方差，更新公式较为复杂。

CMA-ES 通过这些更新近似目标函数\(L(\theta)\)的自然梯度，而无需显式建模费舍尔信息矩阵。